介绍来自李航《统计学习方法》
朴素贝叶斯(naïve Bayes)法是基于贝叶斯定理与特征条件独立假设的分类方法[1]。对于给定的训练数据集,首先基于特征条件独立假设学习输入/输出的联合概率分布;然后基于此模型,对给定的输入x,利用贝叶斯定理求出后验概率最大的输出y。朴素贝叶斯法实现简单,学习与预测的效率都很高,是一种常用的方法。
4.2 朴素贝叶斯法的参数估计
4.2.1 极大似然估计
在朴素贝叶斯法中,学习意味着估计P(Y=ck)和P(X(j)=x(j)|Y=ck)。可以应用极大似然估计法估计相应的概率。先验概率P(Y=ck)的极大似然估计是
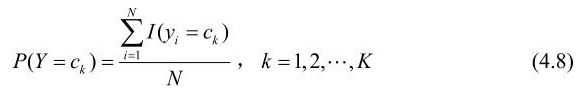
设第j个特征x(j)可能取值的集合为{aj1,aj2,…,ajSj},条件概率P(x(j)=ajl|Y=ck)的极大似然估计是
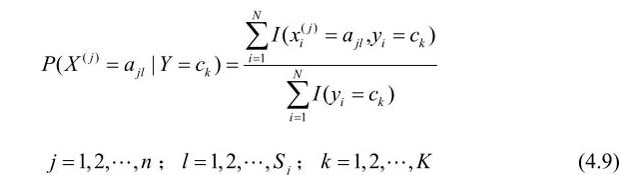
式中,是第i个样本的第j个特征;ajl是第j个特征可能取的第l个值;I为指示函数。
4.2.2 学习与分类算法
下面给出朴素贝叶斯法的学习与分类算法。
算法4.1(朴素贝叶斯算法(naïve Bayes algorithm))
输入:训练数据T={(x1,y1),(x2,y2),…,(xN,yN)},其中,
是第i个样本的第j个特征,
∊{aj1,aj2,…,ajSj},ajl是第j个特征可能取的第l个值,j=1,2,…,n,l=1,2,…,Sj,yi∊{c1,c2,…,cK};实例x;
输出:实例x的分类。
(1)计算先验概率及条件概率
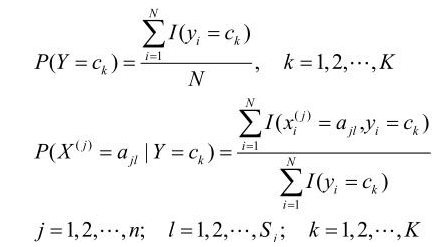
(2)对于给定的实例x=(x(1),x(2),…,x(n))T,计算

(3)确定实例x的类

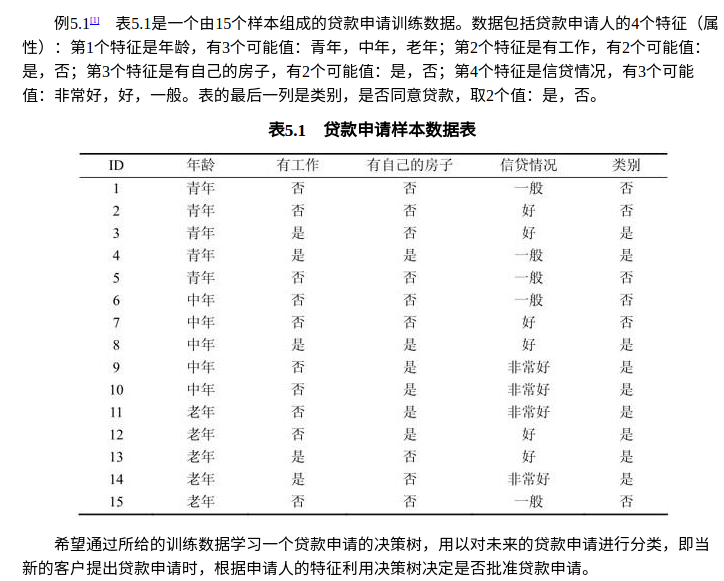
测试数据采用第5章的例子。
1 # coding:utf8 2 3 def NBM(x,y,goal): 4 n=len(y) 5 def getList(x): 6 kx=[] 7 xlist=[] 8 for i in range(1 if type(x[0])!=list else len(x[0])): 9 xlist.append(list(set([a if type(a)!=list else a[i] for a in x ]))) 10 kx.append(len(xlist[i])) 11 return xlist,kx 12 xlist,kx= getList(x) 13 ylist,ky= getList(y) 14 ycount= [y.count(i) for i in ylist[0]] 15 xindex=[[xlist[i].index( goal[i])] for i in range(len(goal))] 16 #print xlist,kx,ylist,ky,ycount,xindex #[[1, 2, 3], ['s', 'm', 'l']] [3, 3] [[1, -1]] [2] [9, 6] [[1], [0]] 17 t=[] 18 p=[] 19 for m in range(ky[0]): 20 for j in range(len(kx)): 21 for i in range(kx[j]): 22 t.append(sum([1 for a in range(n) if xlist[j][i] in x[a] and y[a]==ylist[0][m]])) 23 p.append(t) 24 t=[] 25 #print p #[[2, 3, 4], [1, 4, 4], [3, 2, 1], [3, 2, 1]] 26 px=[] 27 t=1 28 m=0 29 for j in range(ky[0]): 30 for i in range(len(xindex)): 31 t*=(p[m][xindex[i][0]]+1.0)/(ycount[j]+kx[i]) 32 m=m+1 33 px.append(t*(ycount[j]+1.0)/(n+ky[0])) 34 t=1 35 return ylist[0][px.index(max(px))] 36 37 x1 = [[1,'s'],[1,'m'],[1,'m'],[1,'s'],[1,'s'],[2,'s'],[2,'m'],[2,'m'],[2,'l'],[2,'l'],[3,'l'],[3,'m'],[3,'m'],[3,'l'],[3,'l']] 38 y1 = [-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1] 39 goal1 = [2,'s'] 40 x = [["青年", "否", "否", "一般"], 41 ["青年", "否", "否", "好"], 42 ["青年", "是", "否", "好"], 43 ["青年", "是", "是", "一般"], 44 ["青年", "否", "否", "一般"], 45 ["中年", "否", "否", "一般"], 46 ["中年", "否", "否", "好"], 47 ["中年", "是", "是", "好"], 48 ["中年", "否", "是", "非常好"], 49 ["中年", "否", "是", "非常好"], 50 ["老年", "否", "是", "非常好"], 51 ["老年", "否", "是", "好"], 52 ["老年", "是", "否", "好"], 53 ["老年", "是", "否", "非常好"], 54 ["老年", "否", "否", "一般"],] 55 y = ["拒绝","拒绝","同意","同意","拒绝","拒绝","拒绝","同意","同意","同意","同意","同意","同意","同意","拒绝"] 56 goal = ["老年", "否", "否", "好"] 57 print NBM(x,y,goal) #同意 58 print NBM(x1,y1,goal1) #-1