离散信号与系统分析(上)

一、利用MATLAB产生离散信号

1.前言部分

stem(X,Y)：在X的指定点处画出数据序列Y；

stem(X,Y,'filled')：以实心的方式画出茎秆；

axis（[xmin,xmax,ymin,ymax]）：设置当前图形的坐标范围，分别为x轴的最小、最大值，y轴的最小、最大值；

2.实验部分
<代码块>
茎状图

k=-2:1:4;
x=[2,1,1,-1,3,0,2];
stem(k,x);
axis([-3,5,-1.5,3.5])

实心茎状图

k=-2:1:4;
x=[2,1,1,-1,3,0,2];
stem(k,x,'filled');
axis([-3,5,-1.1,3.1])

实验结果图

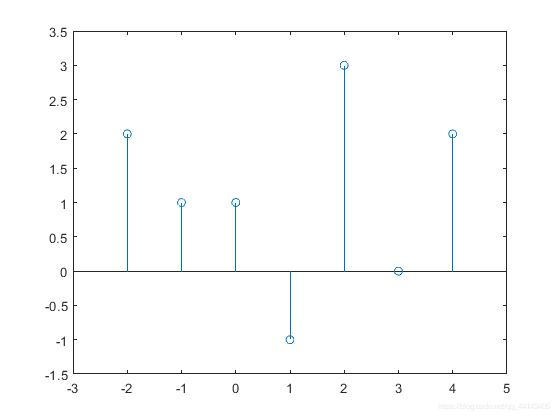
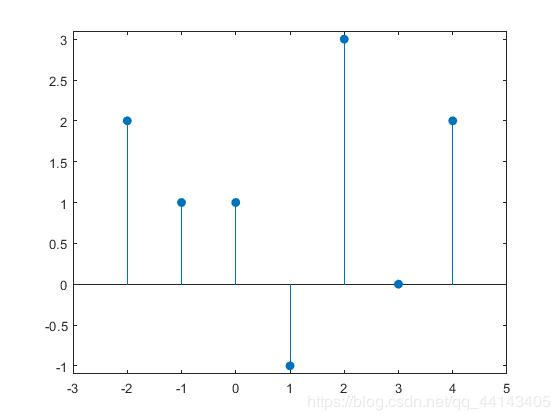
3.结果分析部分

matlab只能表示一个有限长度的序列，而不能表示无穷大的序列。

二、利用MATLAB计算系列卷积与相关

1.前言部分

卷积函数：conv
w = conv(u,v)： 返回向量 u 和 v 的卷积。如果 u 和 v 是多项式系数的向量，对其卷积与将这两个多项式相乘等效。

相关函数：xcorr
c = xcorr(x,y)：返回矢量长度为2*N-1互相关函数序列，其中x和y的矢量长度均为N，如果x和y的长度不一样，则在短的序列后补零直到两者长度相等。

2.实验部分

x=[1,2,3,4];
h=[2,1,3];
y1=conv(x,h)
y2=xcorr(x,h)
y3=conv(h,x)
y4=xcorr(h,x)
y5=xcorr(x,x)
y6=xcorr(h,h)

输出结果

y1 =

 2     5    11    17    13    12

y2 =

-0.0000 3.0000 7.0000 13.0000 19.0000 10.0000 8.0000

y3 =

 2     5    11    17    13    12

y4 =

8.0000   10.0000   19.0000   13.0000    7.0000    3.0000   -0.0000

y5 =

4.0000   11.0000   20.0000   30.0000   20.0000   11.0000    4.0000

y6 =

 6     5    14     5     6

3.结果分析部分

从数字信号处理的角度方面来看，自相关运算可以用卷积运算来代替；在此我就不摆复杂公式了，简单的列举几个结论；

自相关函数：r[-n]=r[n] 偶对称序列，关于x=0对称；可以用xcorr[-n]=xcorr[n]表示；如实验结果y5,y6；

r[n]在n=0处的数值最大；如实验结果y5，y6中30.0000、14分别为其序列中的最大值；

互相关函数xcorr[X,Y]=-xcorr[Y,X]，可见xcorr[X,Y]与xcorr[Y,X]互为其翻转序列；如实验结果y4,y6；