线段树【加强】

题目描述

如题，已知一个数列，你需要进行下面三种操作：

1.将某区间每一个数乘上x

2.将某区间每一个数加上x

3.求出某区间每一个数的和

输入输出格式

输入格式：

 

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

 

输出格式：

 

输出包含若干行整数，即为所有操作3的结果。

 

输入输出样例

输入

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

输出

17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

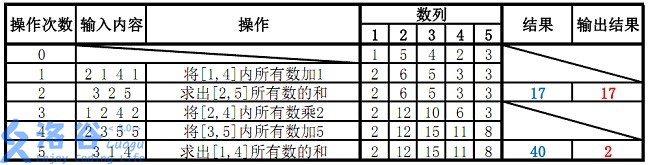
故输出应为17、2（40 mod 38=2）

---

终于调好了线段树（累……

记住：

不开longlong见祖宗，十年oi一场空

code

#include<stdio.h> 
#include<algorithm>
#define ls x<<1
#define rs x<<1|1 
using namespace std;
const int mxn=110000;
int n,m,P,tree[mxn<<2],add[mxn<<2],mul[mxn<<2];
int ql,qr,num,cas;

void build(int x,int l,int r) 
{
    mul[x]=1;
    if(l==r) scanf("%d",&tree[x]);
    else {
        int mid=(l+r)>>1;
        build(ls,l,mid);
        build(rs,mid+1,r);
        tree[x]=tree[ls]+tree[rs];
    }
}

void pd(int x,int l,int r,int mid) {
    if(mul[x]!=1) {
        mul[ls]=mul[ls]*mul[x]%P;
        add[ls]=add[ls]*mul[x]%P;
        tree[ls]=tree[ls]*mul[x]%P;
        mul[rs]=mul[rs]*mul[x]%P;
        add[rs]=add[rs]*mul[x]%P;
        tree[rs]=tree[rs]*mul[x]%P;
        mul[x]=1;
    }
    if(add[x]) {
        add[ls]=(add[ls]+add[x])%P;
        tree[ls]=(tree[ls]+(mid-l+1)*add[x])%P;
        add[rs]=(add[rs]+add[x])%P;
        tree[rs]=(tree[rs]+(r-mid)*add[x])%P;
        add[x]=0;
    }
} 
 
void sol(int x,int l,int r) 
{
    if(ql<=l&&qr>=r) 
    {
        if(cas==1) { //乘 
            mul[x]=mul[x]*num%P;
            add[x]=add[x]*num%P;
            tree[x]=tree[x]*num%P;
        }
        else { //加 
            add[x]=(add[x]+num)%P;
            tree[x]=(tree[x]+num*(r-l+1))%P;
        }
        return ;
    }
    int mid=(l+r)>>1;
    pd(x,l,r,mid);
    if(ql<=mid) sol(ls,l,mid);
    if(qr>mid) sol(rs,mid+1,r);
    tree[x]=tree[ls]+tree[rs];
}

int ask(int x,int l,int r) 
{
    if(ql<=l && qr>=r) return tree[x]; 
    int mid=(l+r)>>1,re=0;
    pd(x,l,r,mid);
    if(ql<=mid) re=(re+ask(ls,l,mid))%P;
    if(qr>mid) re=(re+ask(rs,mid+1,r))%P;
    return re;
}
int main() 
{
    scanf("%d%d%d",&n,&m,&P);
    build(1,1,n);
    while(m--) 
    {
        scanf("%d%d%d",&cas,&ql,&qr);
        if(cas==3) printf("%d
",ask(1,1,n));
        else {
            scanf("%d",&num);
            sol(1,1,n);
        }
    }
    return 0;
}
/*
8 10 571373
5929 7152 8443 6028 8580 5449 8473 4237 
2 4 8 4376
1 2 8 9637
2 2 6 7918
2 5 8 5681
3 2 8
1 1 5 6482
3 1 5
1 5 8 8701
2 5 8 7992
2 5 8 7806

478836
562114
*/