1.本周学习总结
1.思维导图

2.对树结构的认识及学习体会。
感觉树的内容很难,一些逻辑比较难弄懂,而且内容比较多,所以还是得花时间去理解,树不比先前的那些线性结构,多了很多新东西,比如带权路径长度,哈弗曼编码什么的,总之要学起来真的不容易。
2.PTA实验作业
2.1.题目1:6-4 jmu-ds-表达式树
2.1.1设计思路(伪代码)
//观察表达式树会发现数字字符的左孩子右孩子都是空的用于后面的表达式树的运算 //创建两个栈一个是树节点的保存类型一个是字符保存栈 for(int i=0;str[i];i++){ if(字符是数字)创建树节点并且入栈 else { if(字符栈栈顶优先级小于str[i]){ 则进栈字符栈 } else if(字符栈栈顶优先级大于str[i]){ 出栈并且从节点栈中拿出两个; 构树并且放回节点栈中 } else{ 直接出栈 } } 计算表达式 { if(BT->rchild==NULL&&BT->lchild==NULL) return BT->data-'0' else{ a=计算遍历右树 b=计算遍历左树 switch() { case '+':return a+b; case '-':return a-b case '*':returna*b case '/':return a/b } }
2.1.2代码截图
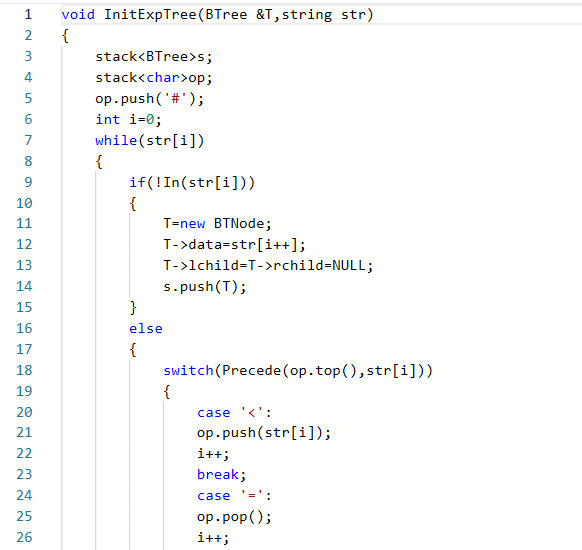


2.1.3本题PTA提交列表说明。
- Q1:在定义栈的时候没用<BTree>类型,Precede函数传进去的是字符也没注意,导致段错误。
- A1:修改定义栈的类型为stack<BTree>,并修改传参。
- Q2:未考虑除数为0的情况,导致部分错误。
- A2:在遇到除号时设计判断函数,除数为0时输出相应字符串。
- Q3:除数为0时按要求输出相应提示,但未加递归出口,还是部分正确。
- A3:在输出错误提示后加上exit(0),来强制退出递归,答案正确。
2.2 题目2:jmu-ds-二叉树叶子结点带权路径长度和
2.2.1设计思路(伪代码)
定义变量str和BT,输入str 利用函数BTree CreateBTree( string str , int n )构造树 { 定义树的指针BT 判断树是否空,如果str[1]=='#'代表根结点不存在,返回NULL,若输入的根结点位置大于str的长度(小于等于0)也返回NULL 给BT一个空间,new BTree;给BT->data赋值str[i]; 利用孩子节点和双亲节点的下标位置关系(若双亲节点下标为i,则左孩子的下标为2i,右孩子下标为2i+1)递归构造树; BT->lchild=CreateBTree( str , 2i ); 和BT->rchild=CreateBTree( str , 2i+1 ); 最后返回根结点指针; } 利用函数void Sum(BTree BT,int &wpl,int h)计算叶子节点的带权路径长度和 { 用类似遍历树的方法先判断根节点是不是叶子节点(左右孩子都为NULL); 利用递归先遍历左子树,每递归一次,增加一层高度h++, 后遍历右子树,同样每递归一次,增加一层高度h++, 当遍历到叶子节点时,用data*高度h,加到wpl中; 输出wpl; }
2.2.2代码截图
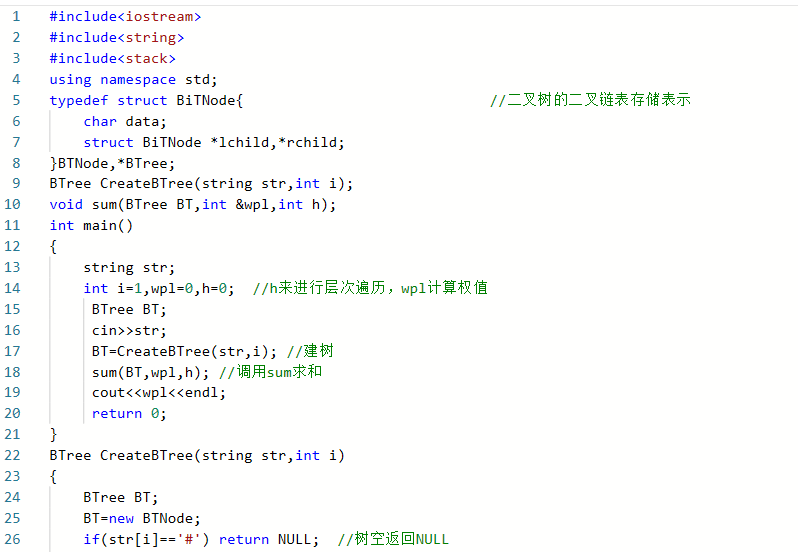
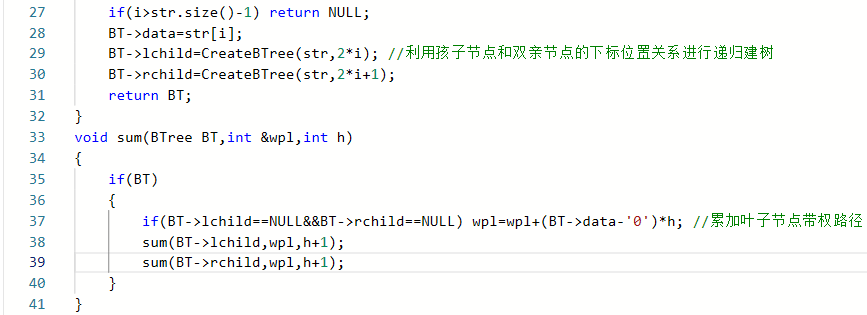
2.2.3本题PTA提交列表说明。
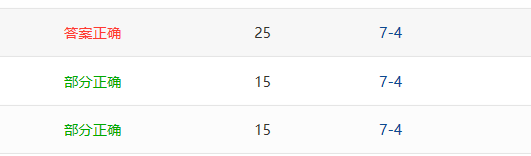

- Q1:计算wpl时没注意是字符形式,需转换为数字,只对了空树这一个测试点。
-
A1:加上data-'0'来转换为字符。
- Q2:传入的是wpl而不是&wpl,由于sum函数是void形式,不可将算过的wpl返回,部分正确。
- A2:传入&wpl,答案正确。
2.3 题目3:根据后序和中序遍历输出先序遍历
2.3.1设计思路(伪代码)
利用函数BTNode Build(int *in,int *post,int n)后序中序构造二叉树的函数 { 首先是传入后序和中序序列和序列长度; 定义结构体指针p,int型变量len; 判断n是否小于0,是,返回NULL; 记录下根结点的值(后序的最后一个为根节点)p=*(post+n-1); T=new BTNode;给T一个空间作为,并赋值; 找到根节点在中序中的位置 并记录下中序中根节点的下标 len=p-in; 利用递归构造左子树和右子树 T->lchild=Build(in,post,len); T->rchild=Build(p+1,post+len,n-len-1); 最后返回T; }
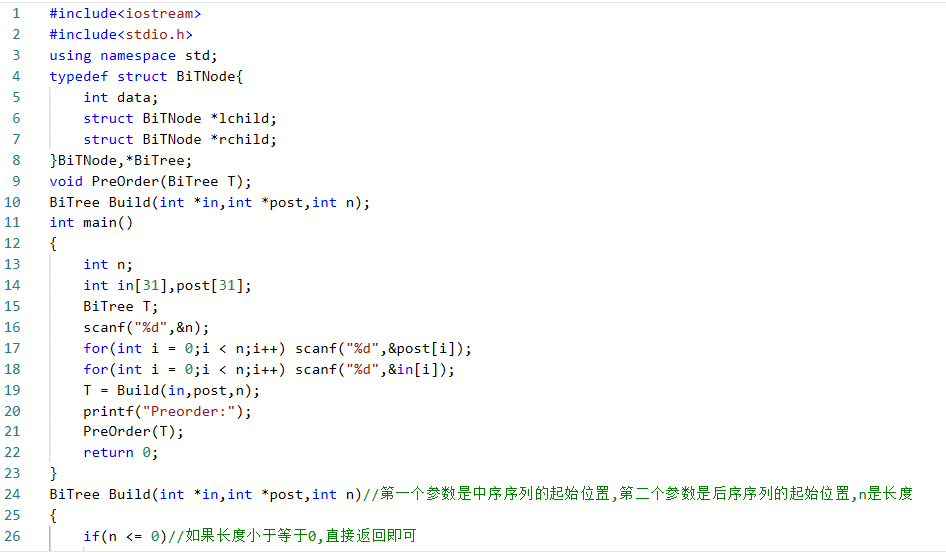
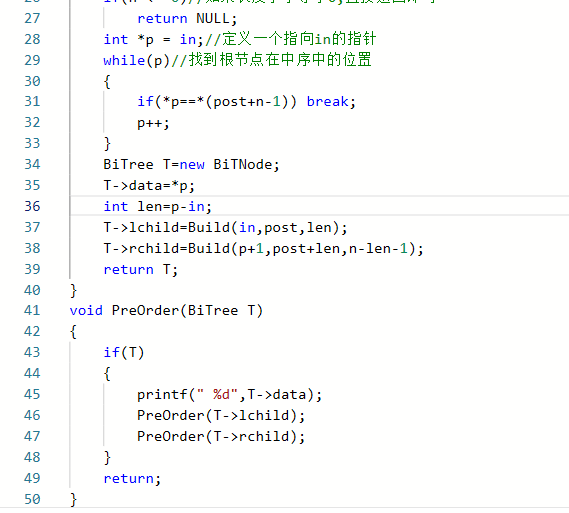
2.3.2代码截图
2.3.3本题PTA提交列表说明。
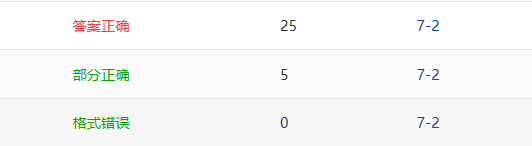
- Q1:数字间的空格没设置好,导致格式错误。
- A1:输出数字前加上空格。
- Q2:在找根节点的位置时没有减去1,导致部分正确。
- A2:设置当*p==*(post+n-1)时停止循环,答案正确。
3、阅读代码
3.1 题目:构造哈夫曼树
给出n个权值,构造出有n个叶子结点的哈夫曼树。
3.2 解题思路
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
3.3 代码截图
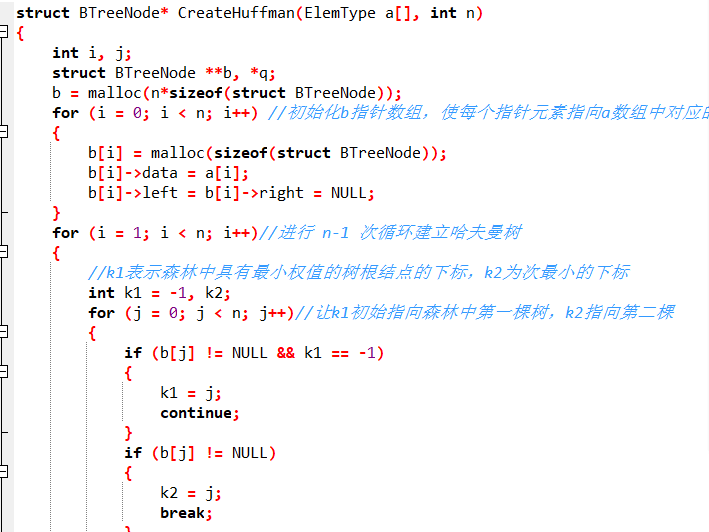

3.4 学习体会
构建哈夫曼树,书本上写的是利用ht数组来记录节点的孩子和双亲,而这篇代码直接构造了一棵链式储存的哈夫曼树,对于7-7的修理牧场来说,只需先构建一个哈夫曼树,在把不是叶子节点的节点data加起来就是题目的答案,思路简单。