Bob has discovered a new quality in himself — he likes to trick people a lot! In particular, Bob wants to try his tricking skills in the shell game.
The shell game involves three identical cups and a single ball. In the beginning the host (that's Bob!) puts the cups upside down and places the ball inside one of the cups. Then he shuffles the cups and the player has to guess where the ball is. The host then lifts that cup, revealing whether the ball was inside or not. The player wins if he makes a correct guess, otherwise the host wins.
The form of each cup is a sliced cone. Formally, the base of the cup is a circle with radius r, and the opening of the cup is a circle with radius R. The height of the cup is equal to h. A ball for the shell game is simply a sphere.
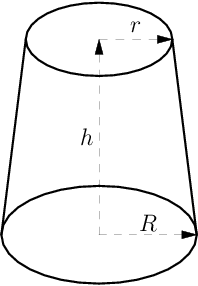
What the player is not going to know is that Bob smeared the inner surface of each cup with glue, resulting in the cup holding the ball when Bob lifts it up — so the player will never win! However, the ball will stick only if it touches the inner surface of a cup. For this reason Bob wants to get the largest possible ball that fits inside the cup when the cup is placed upside down on the table.
Bob has already found three identical cups in his grandmother's locker — now he only has to buy a ball of the required size so that he may start playing the shell game. Help Bob and calculate the largest size of such a ball!
The first line contains three space-separated integers r, R and h, the radii of the base and the opening, and the height of the cup (1 ≤ r < R ≤ 104, 1 ≤ h ≤ 104).
Output a single number — the radius of the largest ball that can fit in the cup. Your answer will be considered correct if its relative or absolute error doesn't exceed 10 - 6.
3 4 8
3.531128874149
已知圆台上底,下底和高,求圆台内存在的最大球体的半径。
圆台只是唬人的。。。可以直接转化为一个梯形内求圆的半径,再注意一下圆半径小于梯形的高的一半即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<stack>
#include<map>
#include<vector>
#include<queue>
using namespace std;
const int MAXN=1e5+10;
const double eps=1e-6;
const int INF=1<<30;
const long long mod=1e9+7;
#define ll long long
#define edl putchar('
')
#define useit ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define FOR(i,a,b) for(int i=a;i<=b;i++)
#define ROF(i,a,b) for(int i=a;i>=b;i--)
#define mst(a) memset(a,0,sizeof(a))
#define mstn(a,n) memset(a,n,sizeof(a))
#define zero(x)(((x)>0?(x):-(x))<eps)
int main()
{
double r,R,h,l,L,k,r1=-1,r2;
scanf("%lf%lf%lf",&r,&R,&h);
k=R-r-sqrt((R-r)*(R-r)+h*h);
if(k>0)
{
r1=h*R/k;
if(r1>h/2)
r1=h/2;
}
k=R-r+sqrt((R-r)*(R-r)+h*h);
r2=h*R/k;
if(r2>h/2)
r2=h/2;
printf("%.10lf
",max(r1,r2));
}
Alice is bored out of her mind by her math classes. She craves for something much more exciting. That is why she invented a new type of numbers, the profacts. Alice calls a positive integer number a profact if it can be expressed as a product of one or several factorials.
Just today Alice received n bills. She wonders whether the costs on the bills are profact numbers. But the numbers are too large, help Alice check this!
The first line contains a single integer n, the number of bills (1 ≤ n ≤ 105). Each of the next n lines contains a single integer ai, the cost on the i-th bill (1 ≤ ai ≤ 1018).
Output n lines, on the i-th line output the answer for the number ai. If the number ai is a profact, output "YES", otherwise output "NO".
7
1
2
3
8
12
24
25
YES
YES
NO
YES
YES
YES
NO
A factorial is any number that can be expressed as 1·2·3·...·k, for some positive integer k, and is denoted by k!.
给你n个询问,求该数字是否能表示为若干个阶乘的乘积。
首先发现20!就超出了数据范围,所以最大的阶乘为19!。
那么依次对数字求余再除阶乘就可以了。
然后我天真的认为大的阶乘能分解为小的阶乘,但小的阶乘不能合成大的阶乘,所以一直优先处理大的阶乘即可,然后就WA了。
直接给出一个反例:
6!*7!=2*3*4*5*6*7!=3*5*6*8!=10*9!
如果直接去算9!会得出这无法表示为阶乘的结论。
所以只能DFS,而这个数据量必须剪枝才行。
另外,如果阶乘的指数为质数,如13!,17!,则只能除去这个阶乘,因为比这小的数字的阶乘必然是错的。
int dfs(ll a,int b)
{
if(t==1)
return 0;
if(a==1)
{
t=1;
return 0;
}
ROF(i,b,2)
{
if(a%f[i-1]==0)
{
dfs(a/f[i-1],i);
if(t==0)
{
FOR(j,0,7)
{
if(pri[j]==i)
return 0;
if(pri[j]>i)
break;
}
}
}
if(t==1)
return 0;
}
return 0;
}
int main()
{
int T;
ll n;
f[0]=1;
FOR(i,1,19)
{
f[i]=f[i-1]*(i+1);
}
scanf("%d",&T);
while(T--)
{
t=0;
scanf("%lld",&n);
dfs(n,20);
if(t==1)
printf("YES
");
else
printf("NO
");
}
return 0;
}