代码地址:
Github:https://github.com/huangbinhong1/031702238
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(小时) |
| Planning | 计划 | 1h | 0.5h |
| Estimate | 估计这个任务需要多少时间 | 22h | 21h |
| Development | 开发 | 5h | 3h |
| Analysis | 需求分析 (包括学习新技术) | 2h | 015h |
| Design Spec | 生成设计文档 | 2h | 3h |
| Design Review | 设计复审 | 0.5h | 1h |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 1.5h | 2h |
| Design | 具体设计 | 4h | 3h |
| Coding | 具体编码 | 1h | 0.5h |
| Code Review | 代码复审 | 1h | 0.5h |
| Test | 测试(自我测试,修改代码,提交修改) | 0.5h | 2h |
| Reporting | 报告 | 1h | 2h |
| Test Repor | 测试报告 | 1h | 1h |
| Size Measurement | 计算工作量 | 1h | 0.5h |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 0.5h | 0.5h |
解题思路
拿到题目的时候的思路其实和现在所写出来的解题思路不太一致,一开始的想法是用一个栈来解决问题,后来发现在C++中我真不知道怎么用栈来存储一个二维数组,后来还是老老实实使用深搜的办法,然后又想了想,我递归还不太熟练,就这么磨着磨着,磨了四五天才出来,最难的是文件的读取和储存,因为在visual studio2017中,是需要考虑到安全问题的,我在DEV C++中运行的好好的代码,拿到VS2017就不行,整了我一天的时间。心累。
我的想法和大家的想法都差不多,用一个函数来判断周围是否有一样的数字

这里是横竖判断函数:
int judge(int *arr, const int n)
{
int i, j, k, pd;
for (i = 0; i < n; i++)
for (j = 0; j <= n - 2; j++)
for (k = j + 1; k < n; k++)
{
if (*(arr + i * n + j) == *(arr + i * n + k))
if (*(arr + i * n + j) != 0)
return 1;
}
for (j = 0; j < n; j++)
for (i = 0; i <= n - 2; i++)
for (k = i + 1; k < n; k++)
{
if (*(arr + i * n + j) == *(arr + k * n + j))
if (*(arr + i * n + j) != 0)
return 1;
}
}
这里是宫格的判断函数://我只列举了9宫格的,这部分代码应该优化,但是没时间了。
if (n == 9)
for (i = 0; i < n; i++)
{
int shu = 0;
if (i < 3)
{
j = 0;
initial(gong, n);
for (; j < 3; j++)
for (k = i * 3; k < (i * 3 + 3); k++)
{
gong[shu] = *(arr + j * n + k);
shu++;
}
// initialshow(gong,n);
// cout<<endl;
pd = judge1(gong, n);
// printf(" %d
",pd);
if (pd == 0)
continue;
else
return pd;
}
else if (i < 6)
{
j = 3;
initial(gong, n);
for (; j < 7; j++)
for (k = (i - 3) * 3; k < ((i - 3) * 3 + 3); k++)
{
gong[shu] = *(arr + j * n + k);
shu++;
}
// initialshow(gong,n);
// cout<<endl;
pd = judge1(gong, n);
// printf(" %d
",pd);
if (pd == 0)
continue;
else
return pd;
}
else
{
j = 6;
initial(gong, n);
for (; j < 9; j++)
for (k = (i - 6) * 3; k < ((i - 6) * 3 + 3); k++)
{
gong[shu] = *(arr + j * n + k);
shu++;
}
// initialshow(gong,n);
// cout<<endl;
pd = judge1(gong, n);
//printf(" %d
",pd);
if (pd == 0)
continue;
else
return pd;
}
}
在宫格的判断中,我引入一个新的宫格数组,将宫格中的数移到宫格数组中,然后用一个判断函数来宫格数组中有无重复数字。
下面是宫格判断:
int judge1(int *arr, const int n)
{
int i, j;
for (i = 0; i < n - 2; i++)
for (j = i + 1; j < n; j++)
{
if (*(arr + i) == *(arr + j))
if (*(arr + i) != 0)
return 1;
}
return 0;
}
说完了判断之后就是填数了,一个正常的回溯算法:
int tianshu(int *arr, const int n)
{
int i, j, shu, x, s;
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
if (*(arr + i * n + j) == 0)
{
//printf("%d %d
",i,j);
for (shu = 1; shu <= n; shu++)
{
if (xx == 0)
return 0;
*(arr + i * n + j) = shu;
x = judge(arr, n);
if (x == 1)
if (shu == n)
{
*(arr + i * n + j) = 0;
return 1;
}
else
{
continue;
}
s = tianshu(arr, n);
if (s == 1)
if (shu == n)
{
*(arr + i * n + j) = 0;
return 1;
}
else
continue;
if (s == 0)
{
xx = 0;
return 0;
}
}
}
}
}
return judge(arr, n);
}
代码评测:

通过
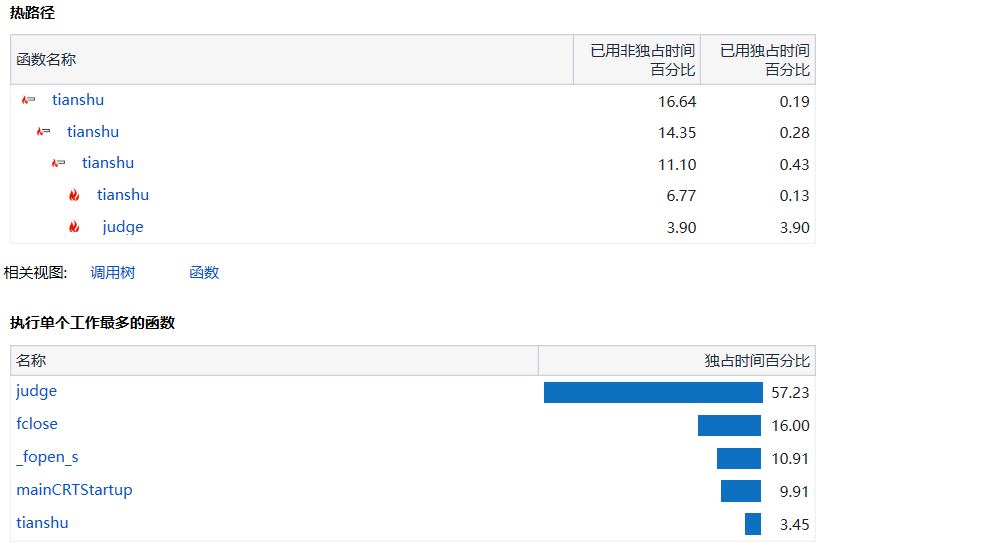
下面是函数时间分析
judge占主要时间是可以预见的。毕竟是回溯算法。
示例测试:

感想:
很多的东西都是现学的,每个人遇到的麻烦都不一样,只能自己一点慢慢的摸索,在摸索的过程中也会学会更多有趣能提升自己的东西,这就是好的吧。