题目详情
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:
输入: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
题目解析
关键是找到状态方程, 我们设置dp[i]表示整数i的最大乘积, 那么把问题分成子问题, 我们发现dp[i] 与前面的dp[1] ~ dp[i-1]都有关系, 关系很容易找到
dp[i] = max(j * (i-j), j * dp[i - j]) j = 1,2 ······ i -1
而初始条件dp[1] = 1, dp[2] = 2, dp[3] = 3
为什么要加上 j * (i-j)的比较呢, 是为了处理dp[i] < i的情况, 例如
n=4, 那么如果不考虑 j * (i-j), 因为dp[2] = 1 <2, 所以最终的结果为3, 但是其实把4分成2 * 2, 最终结果为4. 所以要加上 j * (i-j) 直接把i分成两个数字i, j-i,的情况。
那么可以由此得到第一种dp代码
代码一 动态规划
class Solution {
public:
int integerBreak(int n) {
vector <int> dp(n +1, 0);
int tmp = 0;
dp[0] = 0;
dp[1] = 1;
dp[2] = 1;
for (int i = 3; i <= n ; i++) {
tmp = 0;
for (int j = 1; j <= i - 1; j++) {
tmp = max(tmp, max(dp[j] * (i-j), j * (i - j)));
}
dp[i] = tmp;
}
return dp[n];
}
};
时间复杂度为0(n^2)
代码2 数学推倒
有一些其他的博客给了更加速度快的算法, 有一种是利用数学推导, 得出要想使乘积最大, 只需要尽可能的多分成3, 其次是二
数学推导过程
由均值不等式(n个数的算术平均数大于等于它们的几何平均数):
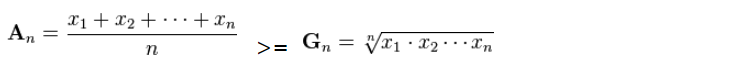
得:当把输入的n拆分成几个相等的数时它们的积最大。
那么问题来了,拆分成几个呢?
为了方便使用导数,我们先假设我们可以把n拆分成实数。那么设每一个数为x,则一共有n/x个数。
设它们的积为f(x),则f(x)=x(n/x),那么怎么求f(x)最大值呢?求导数!
f′(x)=(n/x2) * x(n/x) * (1-lnx)
当x=e时取极大值。
而我们题目里规定x为整数,那么我们只需要取的x越靠近e越好。那么2<e<3,而且e=2.71828…,所以取3是最好的,如果取不到3就取2。
幂运算复杂度为O(lgn),所以这个算法复杂度为O(lgn)。
代码如下
class Solution {
public:
int integerBreak(int n) {
if(n == 2)
return 1;
else if(n == 3)
return 2;
else if(n%3 == 0)
return pow(3, n/3);
else if(n%3 == 1)
return 2 * 2 * pow(3, (n - 4) / 3);
else
return 2 * pow(3, n/3);
}
};