转载地址
https://blog.csdn.net/greedystar/article/details/80343841
目录
一、问题描述
旅行商问题是图论中的一个著名问题。
假设有一个旅行商人要拜访N个城市,要求他从一个城市出发,每个城市最多拜访一次,最后要回到出发的城市,保证所选择的路径长度最短。
二、算法描述
(一)算法简介
遗传算法(GeneticAlgorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,通过模拟自然进化过程搜索最优解。遗传算法是从代表问题可能潜在的解集的一个种群(population)开始的,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择个体,并借助于自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码(decoding),可以作为问题近似最优解。(摘自百度百科)。
(二)遗传算子
遗传算法中有选择算子、交叉算子和变异算子。
选择算子用于在父代种群中选择进入下一代的个体。
交叉算子用于对种群中的个体两两进行交叉,有Partial-Mapped Crossover、Order Crossover、Position-based Crossover等交叉算子。
变异算子用于对种群中的个体进行突变。
(三)算法步骤描述
遗传算法的基本运算过程如下:
1. 初始化:设置进化代数计数器t=0、设置最大进化代数T、交叉概率、变异概率、随机生成M个个体作为初始种群P
2. 个体评价:计算种群P中各个个体的适应度
3. 选择运算:将选择算子作用于群体。以个体适应度为基础,选择最优个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代
4. 交叉运算:在交叉概率的控制下,对群体中的个体两两进行交叉
5. 变异运算:在变异概率的控制下,对群体中的个体两两进行变异,即对某一个体的基因进行随机调整
6. 经过选择、交叉、变异运算之后得到下一代群体P1。
重复以上1-6,直到遗传代数为T,以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。
三、求解说明
(一)优化目标
给定二维数据int[][]pos用于存储各个城市的坐标,采用欧式距离代表城市之间的距离。利用遗传算法,找到不重复遍历所有城市的路径中,所走距离最短的路径。
(二)选择算子
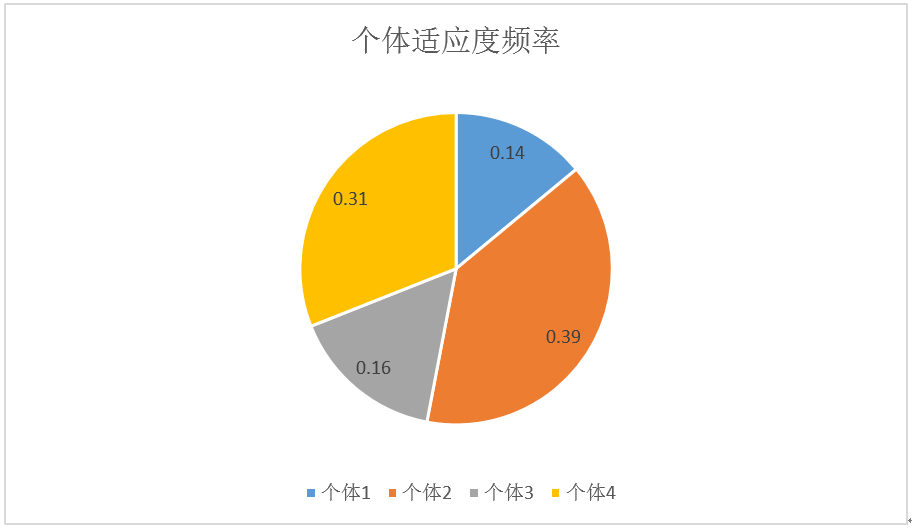
选择算子采用轮盘赌选择,以每个个体的适应度为基础,为每个个体计算累积概率。
个体1、2、3、4的个体适应度如上图所示。
适应度计算规则:染色体代表的路径实际距离作为个体的适应度,如下(distence[x][y]表示城市x到y的距离)
染色体 0 2 1 3,适应度为distence[0][2] + distence[2][1] + distence[1][3] + distence[3][0]
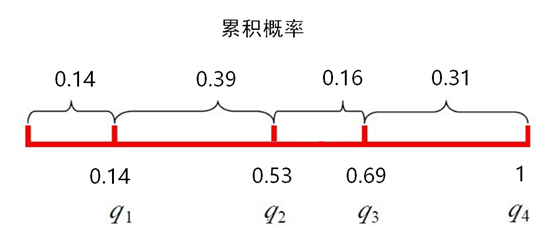
qa 表示个体a的累积概率,如上图所示个体1、2、3、4的累积概率分别为0.14、0.53、0.69、1
随机生成一个0到1的浮点数f,若 qa < f <= qb,则个体b被选中。
(三)交叉算子
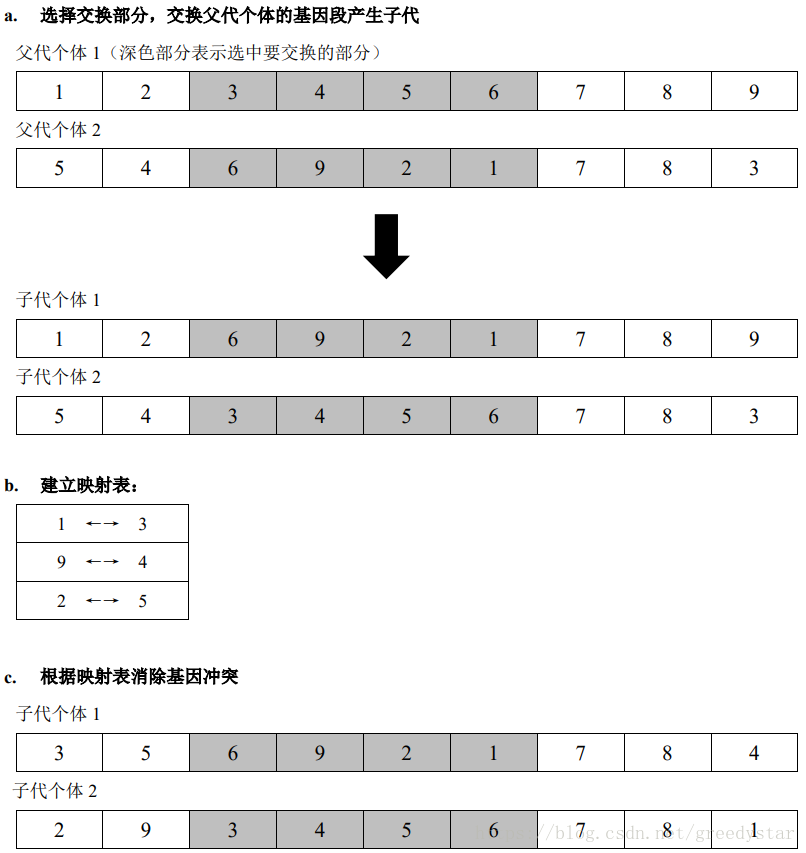
1. Partial-Mapped Crossover(部分映射交叉)
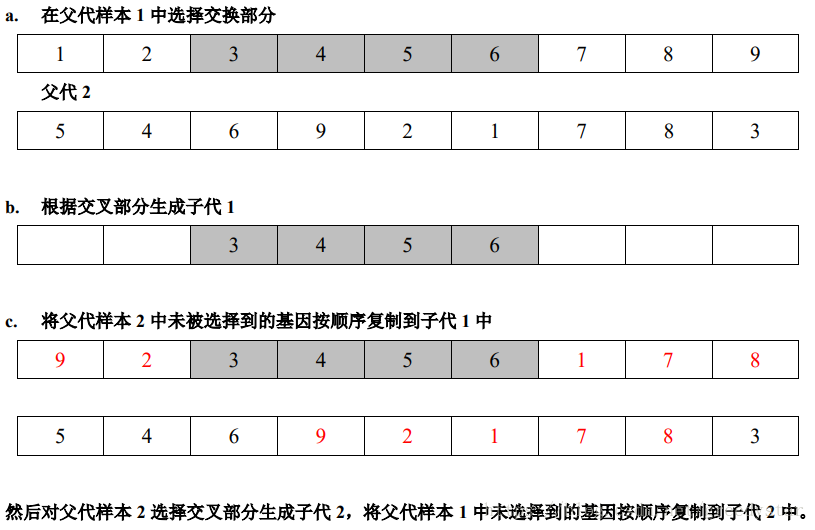
2. Order Crossover(顺序交叉)
3. Position-based Crossover(基于位置的交叉)
(四)变异算子
变异算子随机进行多次,每次在个体基因序列中选择两个位置的基因进行交换。
四、参考资料
五、源代码
源码地址:遗传算法求解TSP问题(参考自基于遗传算法求解TSP问题(JAVA))