| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
|---|---|
| 这个作业的地址 | DS博客作业02--栈和队列 |
| 这个作业的目标 | 学习栈和队列的结构设计及运算操作 |
| 姓名 | 付峻霖 |
0.PTA得分截图

1.本周学习总结
1.1 栈
⭐栈结构的定义和特点
- 栈的顺序存储是由数组来实现的
- 只允许在栈顶进行插入删除操作,另一端为栈底
- 栈是后进先出的线性表
- 线性表的表尾是栈顶,而不是栈底
- 无论是进栈还是出栈,均在栈顶操作,栈底是固定的
⭐栈的抽象数据类型
ADT 栈(stack)
Data
同线性表。元素具有相同的类型,相邻元素具有前驱和后继关系。
Operation
InitStack(*S):初始化操作,建立一个空栈S。
DestroyStack(*S):若栈存在,则销毁它。
ClearStack(*S):将栈清空。
StackEmpty(S):若栈为空,返回true,否则返回false。
GetTop(S,*e):若栈存在且非空,用e返回S的栈顶元素。
Push(*S,e):若栈S存在,插入新元素e到栈S中并成为栈顶元素
Pop(*S,*e):删除栈S中栈顶元素,并用e返回其值。
StackLength(S):返回栈S的元素个数
endADT
Q:什么时候函数操作要用‘*’号?
A:调用函数过后,内容有被修改就要用‘*’号
1.1.1 顺序栈
⭐顺序栈的图形
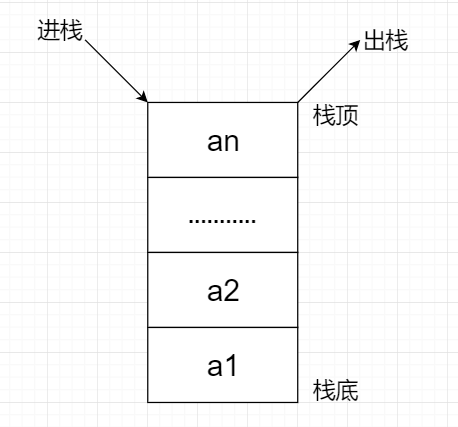
⭐顺序栈的结构定义
typedef int SElemType;
/*顺序栈结构*/
typedef struct
{
SElemType data[MAXSIZE];
int top; /*用于栈顶指针*/
}SqStack;
⭐顺序栈的基本操作
- 初始化栈
void InitStack(SqStack* S)
{
S=new SqStack; //分配一个顺序栈空间,首地址放在S中
S->top=-1; //栈顶指针置为-1
}
- 进栈操作
/*插入元素e为新的栈顶元素*/
bool Push(SqStack* S, SElemType e)
{
if (S->top == MAXSIZE - 1)/*栈满*/
return ERROR;
S->top++; /*栈顶指针增加一*/
S->data[S->top] = e; /*将新插入元素赋值给栈顶空间*/
return OK;
}
- 出栈操作
/*若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK,否则返回ERROR*/
bool Pop(SqStack* S, SElemType* e)
{
if (S->top == -1) /*栈空*/
return ERROR;
*e = S->data[S->top]; /*将要删除的栈顶元素赋值给e*/
S->top--; /*栈顶指针减一*/
return OK;
}
- 销毁栈
void DestroyStack(SqStack* S)
{
free(S);
}
1.1.2 顺序栈--两栈共享空间
栈的顺序存储还是很方便的,在插入删除时不需要移动元素,不过它有一个缺陷,必须事先确定数组大小,这很可能造成资源浪费
⭐两栈共享空间的图形
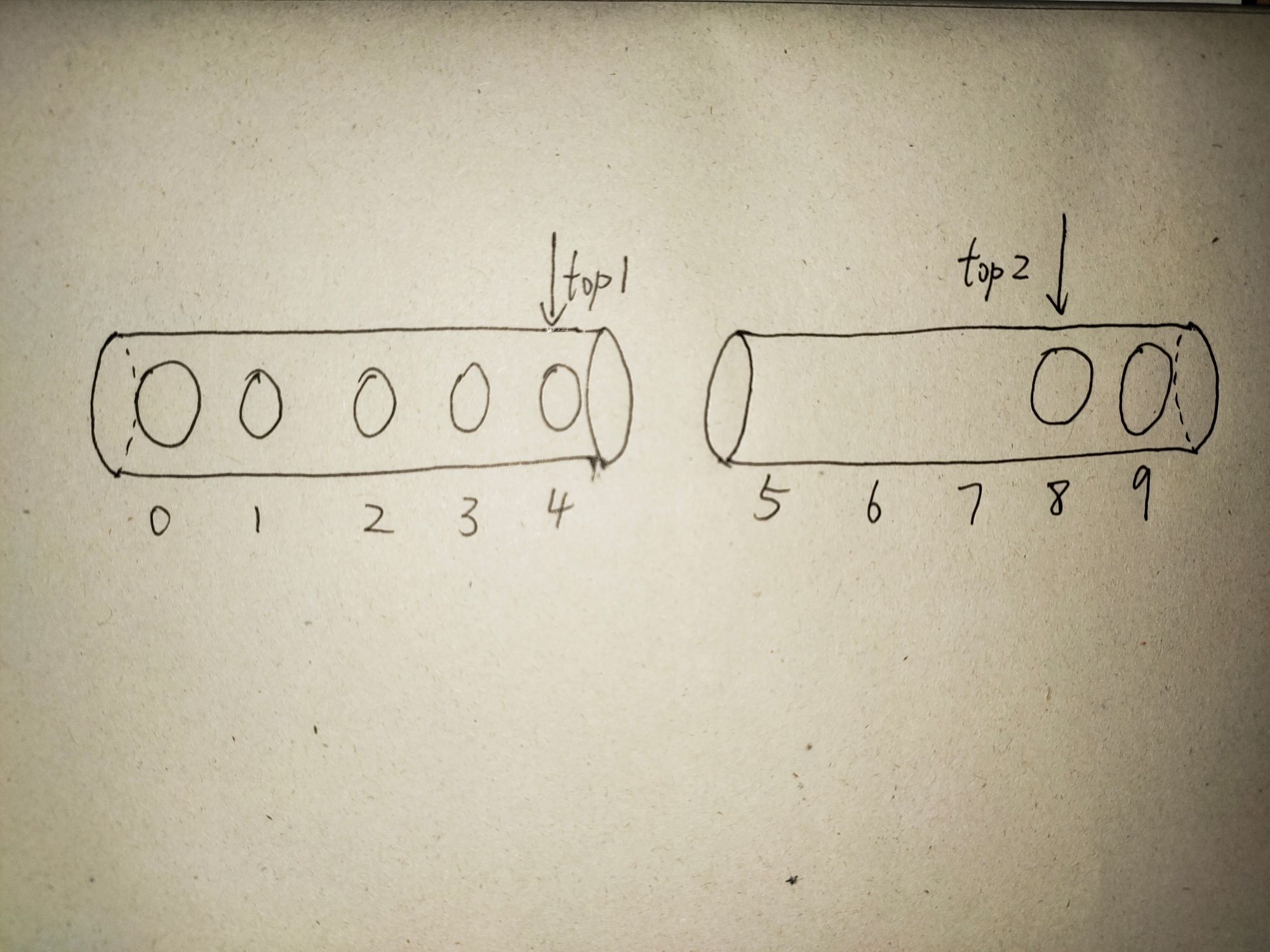
⭐两栈共享空间的结构定义
/*两栈共享空间结构*/
typedef struct
{
SElemType data[MAXSIZE];
int top1; /*栈1的栈顶指针*/
int top2; /*栈2的栈顶指针*/
}SqDoubleStack;
⭐两栈共享空间的基本操作
- 插入操作
/*插入元素e为新的栈顶元素*/
bool Push(SqDoubleStack* S, SElemType e, int stackNumber)
{
if (S->top1 + 1 == S->top2) /*栈已满,不能再push新元素了*/
return ERROR;
if (stackNumber == 1) /*栈1有元素进栈*/
S->data[++S->top1] = e; /*若是栈1则先top1+1后给数组元素赋值*/
else if (stackNumber == 2) /*栈2有元素进栈*/
S->data[--S->top2] = e; /*若是栈2则先top2-1后给数组元素赋值*/
return OK;
}
- 删除操作
/*若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR*/
bool Pop(SqDoubleStack* S, SElemType *e, int stackNumber)
{
if (stackNumber == 1)
{
if (S->top1 == -1)
return ERROR; /*说明栈1已经是空栈,溢出*/
*e = S->data[S->top1--]; /*将栈1的栈顶元素出栈*/
}
if (stackNumber == 2)
{
if (S->top2 == -1)
return ERROR; /*说明栈2已经是空栈,溢出*/
*e = S->data[S->top2++]; /*将栈2的栈顶元素出栈*/
}
return OK;
}
1.1.3 链式栈
⭐链式栈的图形
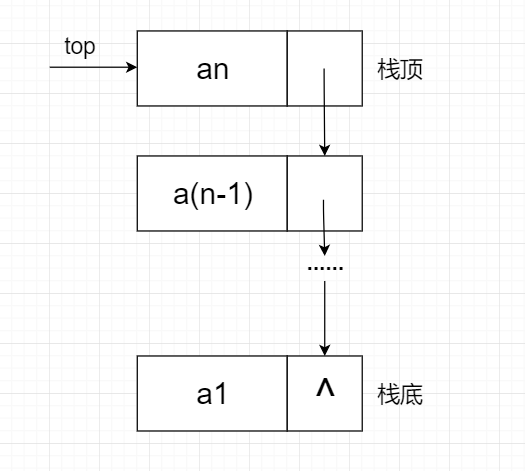
⭐链式栈的结构定义
/*链栈结构*/
typedef struct StackNode
{
SElemType data; //数据域
struct StackNode* next;//指针域
}StackNode,*LinkStackPtr; //链栈结点类型
typedef struct
{
LinkStackPtr top;
int count;
}LinkStack;
⭐链式栈的基本操作
- 初始化栈
void InitStack(StackNode* S)
{
S = new StackNode;
S->next = NULL;
}
- 进栈操作
/*插入元素e为新的栈顶元素*/
bool Push(LinkStack* S, SElemType e)
{
LinkStackPtr s = new StackNode;
s->data = e;
s->next = S->top;/*把当前的栈顶元素赋值给新结点的直接后继*/
S->top = s; /*将新的结点s赋值给栈顶指针*/
S->count++;
return OK;
}
- 出栈操作
bool Pop(LinkStack* S, SElemType* e)
{
LinkStackPtr p;
if (StackEmpty(*S))
return ERROR;
*e = S->top->data;
p = S->top; /*将栈顶结点赋值给p*/
S->top = S->top->next; /*使得栈顶指针下移一位,指向后一结点*/
free(p); /*释放结点p*/
S->count--;
return OK;
}
1.2 栈的应用
1.2.1 斐波那契数列的实现--兔子繁衍后代
⭐题目
兔子在出生两个月后,就右繁衍能力,一对兔子每个月能生出一对小兔子来。假设所有兔子都不死,那么一年后可以繁衍多少兔子呢?
⭐题目分析
第一个月小兔子没有繁殖能力,所以还是一对,第二个月生下一对小兔子,总共两对,第三个月,老兔子又生一对,小兔子没有繁衍能力,总共三对······
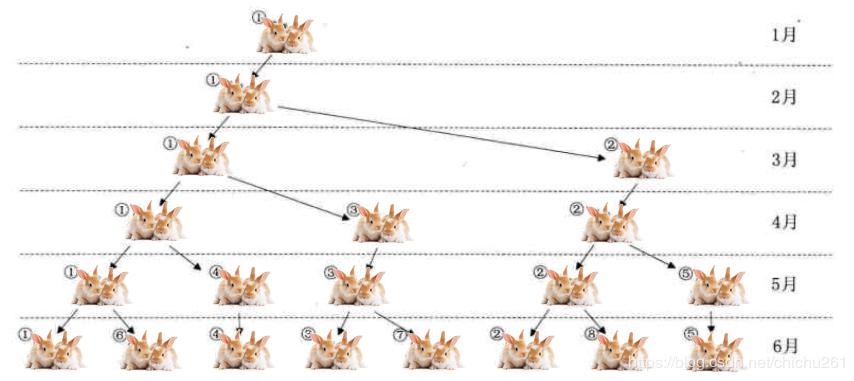
- 数学定义
F(n)=F(n-1)+F(n-2)
⭐代码实现
/*斐波那契的递归函数*/
int Fbi(int i)
{
if (i < 2) /*0月零对兔子,1月一对兔子*/
return i == 0 ? 0 : 1; //特殊处理
return Fbi(i - 1) + Fbi(i - 2);
}
int main()
{
int i;
printf("递归显示斐波那契数列:
");
for (i = 0; i <= 12; i++) //打印每个月 繁殖的小兔子对数
printf("%d", Fbi(i));
return 0;
}
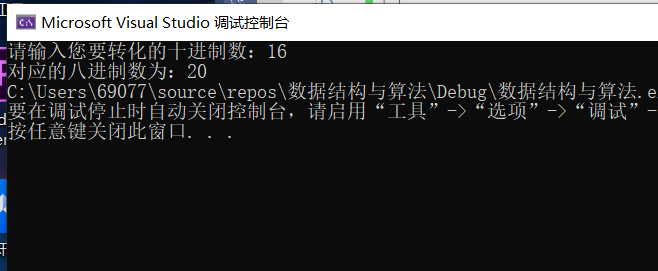
1.2.2 十进制数转八进制数
十进制数转八进制数码云
⭐输入样例与输出样例
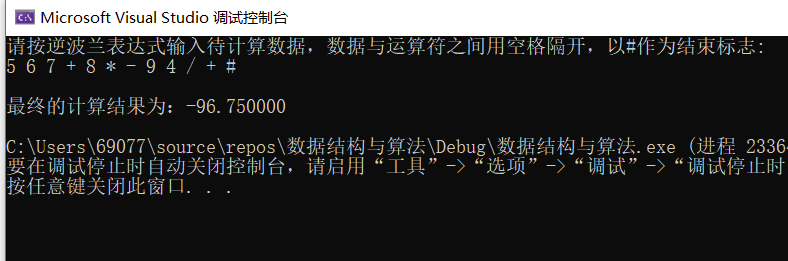
1.2.3 逆波兰计算结果
后缀表达式计算结果码云
⭐输入样例与输出样例
1.3 队列
⭐队列结构的定义和特点
- 队列是一种先进先出的线性表
- 允许插入的一端称为队尾,允许删除的一端称为队头
- 插入数据只能再队尾进行,删除数据只能在队头进行
⭐队列的抽象数据类型
ADT 队列(Queue)
Data
同线性表。元素具有相同的类型,相邻元素具有前驱和后继关系。
Operation
InitQueue(*Q):初始化操作,建立一个空队列Q。
DestroyQueue(*Q):若队列Q存在,则销毁它。
ClearQueue(*Q):将队列Q清空。
QueueEmpty(Q):若队列Q为空,返回true,否则返回false。
GetHead(Q,*e):若队列Q存在且非空,用e返回队列Q的队头元素。
EnQueue(*Q,e):若队列Q存在,插入新元素e到队列Q中并成为队尾元素。
DeQueue(*Q,*e):删除队列Q中队头元素,并用e返回其值
QueueLenghth(Q):返回队列Q的元素个数。
endADT
Q:什么时候函数操作要用‘*’号?
A:调用函数过后,内容有被修改就要用‘*’号
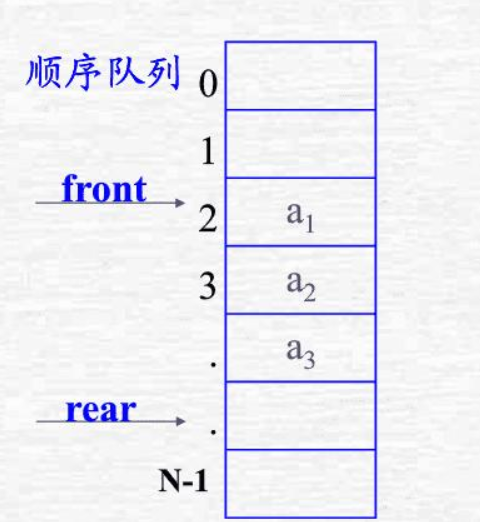
1.3.1 顺序队列
⭐顺序队列的图形
⭐顺序队列的结构定义
typedef int QElemType;
/*顺序队列的存储结构*/
typedef struct
{
QElemType data[MAXSIZE];
int front; /*头指针*/
int rear; /*尾指针,若队列不空,指向队列尾元素的下一个位置*/
}SqQueue;
⭐顺序队列的基本操作
- 初始化队列
/*初始化一个空队列Q*/
void InitQueue(Queue& Q)
{
Q = new Queue;//动态申请内存
Q->front = 0;
Q->rear = 0;
}
- 入队操作
/*若队列未满,则插入元素e为Q新的队尾元素*/
bool EnQueue(SqQueue* Q, QElemType e)
{
if (Q->rear + 1 == MAXSIZE)/*队列满的判断*/
return ERROR;
Q->data[Q->rear] = e; /*将元素e赋值给队尾*/
Q->rear = Q->rear + 1; /*rear指针向后移一位置*/
return OK;
}
- 出队操作
/*若队列不空,则删除Q中队头元素,用e返回其值*/
bool DeQueue(SqQueue* q, Elemtype* e)
{
if (Q->front == Q->rear) /*队列空的判断*/
return ERROR;
*e = Q->data[Q->front]; /*将队头元素赋值给e*/
Q->front = Q->front + 1; /*front指针向后移一位置*/
return OK;
}
1.3.2 循环队列
⭐循环队列的图形

⭐循环队列的结构定义
typedef int QElemType;
/*循环队列的顺序存储结构*/
typedef struct
{
QElemType data[MAXSIZE];
int front; /*头指针*/
int rear; /*尾指针,若队列不空,指向队列尾元素的下一个位置*/
}SqQueue;
⭐循环队列的基本操作
- 初始化队列
/*初始化一个空队列Q*/
bool InitQueue(Queue& Q)
{
Q->front = 0;
Q->rear = 0;
return OK;
}
- 入队操作
/*若队列未满,则插入元素e为Q新的队尾元素*/
bool EnQueue(SqQueue* Q, QElemType e)
{
if ((Q->rear + 1)%MAXSIZE == Q->front)/*队列满的判断*/
return ERROR;
Q->data[Q->rear] = e; /*将元素e赋值给队尾*/
Q->rear = (Q->rear + 1) % MAXSIZE; /*rear指针向后移一位置*/
/*若到最后则转到数组头部*/
return OK;
}
- 出队操作
/*若队列不空,则删除Q中队头元素,用e返回其值*/
bool DeQueue(SqQueue* q, Elemtype* e)
{
if (Q->front == Q->rear) /*队列空的判断*/
return ERROR;
*e = Q->data[Q->front]; /*将队头元素赋值给e*/
Q->front = (Q->front + 1) % MAXSIZE; /*front指针向后移一位置*/
/*若到最后则转到数组头部*/
return OK;
}
- 求队列长度
/*返回Q的元素个数,也就是队列的当前长度*/
int QueueLength(SqQueue Q)
{
return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
}
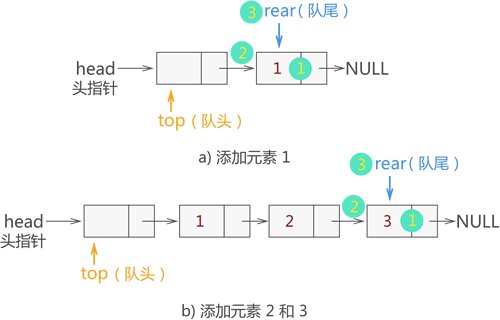
1.3.3 链式队列
⭐链式队列的图形
⭐链式队列的结构定义
typedef int QElemType;
typedef struct QNode /*结点结构*/
{
QElemType data;
struct QNode* next;
}QNode, * QueuePtr;
typedef struct /*队列的链表结构*/
{
QueuePtr front, rear; /*队头、队尾指针*/
}LinkQueue;
⭐链式队列的基本操作
- 入队操作
/*插入元素e为Q的新的队尾元素*/
bool EnQueue(LinkQueue* Q, QElemType e)
{
QueuePtr s = new QNode;
if (!s) /*存储分配失败*/
exit(OVERFLOW);
s->data = e;
s->next = NULL;
/*尾插法*/
Q->rear->next = s;/*把拥有元素e的新结点s赋值给原队尾结点的后继*/
Q->rear = s; /*把当前的s设置为队尾结点,rear指向s*/
return OK;
}
- 出队操作
/*若队列不空,删除Q的队头元素,用e返回其值,并返回OK,否则返回ERROR*/
bool DeQueue(LinkQueue* Q, QElemType* e)
{
QueuePtr p;
if (Q->front == Q->rear)
return ERROR;
p = Q->front->next; /*将要删除的队头结点暂存给p*/
*e = p->data; /*将要删除的队头结点的值赋值给e*/
Q->front->next = p->next; /*将原队头结点的后继p->next赋值给头结点后继*/
if (Q->rear == p) /*若队头就是队尾,则删除后将rear指向头结点*/
Q->rear = Q->front;
free(p);
return OK;
}
⭐队列应用
1.3.1 6-3 jmu-ds-舞伴问题 (20 分)
⭐题目
假设在周末舞会上,男士和女士们分别进入舞厅,各自排成一队。跳舞开始,依次从男队和女队队头各出一人配成舞伴,若两队初始人数不同,则较长那一队未配对者等待下一轮舞曲。现要求写一算法模拟上述舞伴配对问题。
⭐思路
- 创建俩队列分别放男士和女士
- 俩队列同时弹出一个人,组成舞伴
⭐核心代码
/*将Person里的人 分别放到Mdancers,Fdancers两个队列中*/
void DancePartner(Person dancer[], int num)//舞蹈合作伙伴
{
for (int i = 0; i < num; i++)
{
if (dancer[i].sex == 'M')
{ //男生在男栈
EnQueue(Mdancers, dancer[i]);
}
else
{ //女生在女栈
EnQueue(Fdancers, dancer[i]);
}
}
while (QueueEmpty(Mdancers) != 1 && QueueEmpty(Fdancers) != 1)
{ //当 两个栈都不为空
Person x, y;
DeQueue(Mdancers, x);//弹出一个男生
DeQueue(Fdancers, y);//弹出一个女生
cout << y.name << " " << x.name << endl;
}
}
2.PTA实验作业(4分)
2.1 符号配对
2.1.1 解题思路及伪代码
⭐解题思路
- 遍历字符串,把括号之外的东西全部忽略
- 只要是左符号就入栈。
- 只要当前符号与栈顶符号配对成功,就出栈
- 最后进行条件判断,flag的状态与栈是否为空
⭐伪代码
for (遍历字符串)
{
if (是左括号)
入栈
else if (栈空且当前位置为右符号)//配对失败
flag = 1;
break; 结束
else if (栈顶元素与当前位置符号刚好配对)//配对成功
栈顶元素出栈
}
if (flag == 1)
右符号剩余
else if (flag == 0 且 栈空)
无剩余,完全配对成功
else 栈不为空
左符号剩余
return 0;
2.1.2 总结解题所用的知识点
- stack模板各类函数pop,push,empty的应用
- 分类讨论思想,当它是左符号时入栈,为右符号时出栈,还要考虑特殊情况
- 巧用flag与栈的状态表示配对结果
2.2 银行业务队列简单模拟
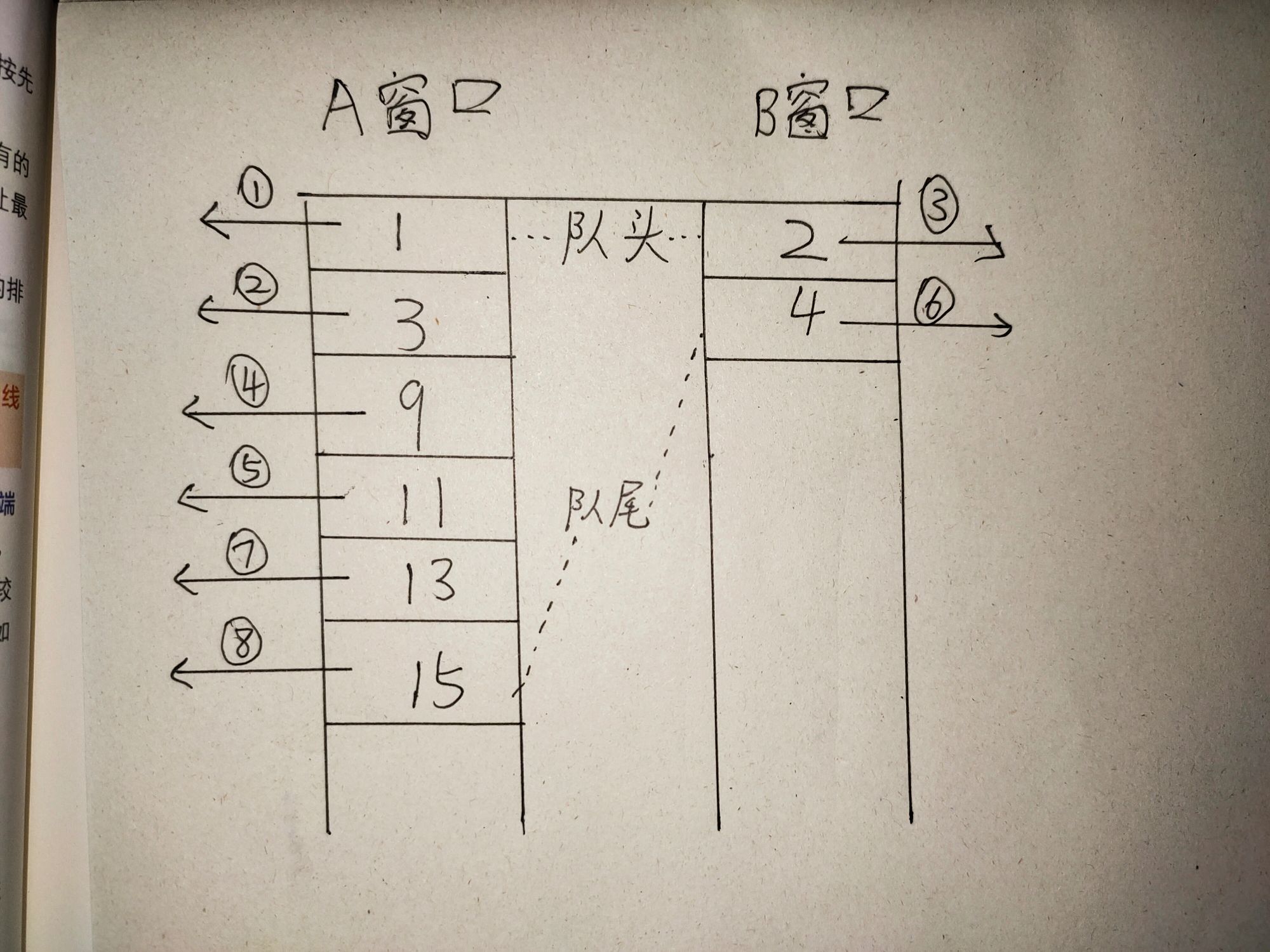
2.2.1 解题思路及伪代码
⭐解题思路
- 首先把这些数字分配到A或B队列中
- 如果A是奇数,那就直接删除A队头
- 如果A是偶数,那就A先走,B再走
⭐伪代码
/*让所有顾客进入队列*/
for (顾客总数)
输入每个数字
if (数字为奇数)
入A队列
else 数字为偶数
入B队列
/*头部空格单独处理*/
if (!A.empty())
打印A队头
删除A队头
i = 1;//处理完的顾客人数
else
打印B队头
删除B队头
/*正常处理*/
while (A不为空 或 B不为空)
i++; //处理完的顾客人数+1
if (奇数)
if (A队列不为空)
打印A队头
删除A队头
else 偶数
/*A先删除,B再删除*/
if (A队列不为空)
打印A队头
删除A队头
if (B队列不为空)
打印B队头
删除B队头
2.2.2 总结解题所用的知识点
- queue模板各类函数pop,push,empty的应用
- 关于奇数偶数的处理,用i来计数,奇数出A,偶数出A再出B
3.用两个栈实现队列
3.1 题目及解题代码
-
题目
-
代码
class CQueue {
Stack<Integer> in;
Stack<Integer> out;
public CQueue() {
in = new Stack<Integer>();
out = new Stack<Integer>();
}
public void appendTail(int value) {
in.push(value);
}
public int deleteHead() {
if(in.isEmpty()&&out.isEmpty()) return -1;
if(out.isEmpty())
while(!in.isEmpty())
out.push(in.pop());
return out.pop();
}
}
作者:Jokar兄
链接:https://www.bilibili.com/video/BV1E54y127LP?t=56
来源:哔哩哔哩(bilibili)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3.2 该题的设计思路及伪代码
⭐题意解读
通过两个先进后出的栈,实现一个先进先出的队列
⭐设计思路
- 创建两个栈,栈in用于存储存入的元素,栈out用于存储用于弹出的元素
- 比如123,栈in存放完元素后栈顶为3,将栈in中的元素弹入栈out中,栈out的栈顶元素为1,再弹出栈out的123,实现了输入为123,输出也为123
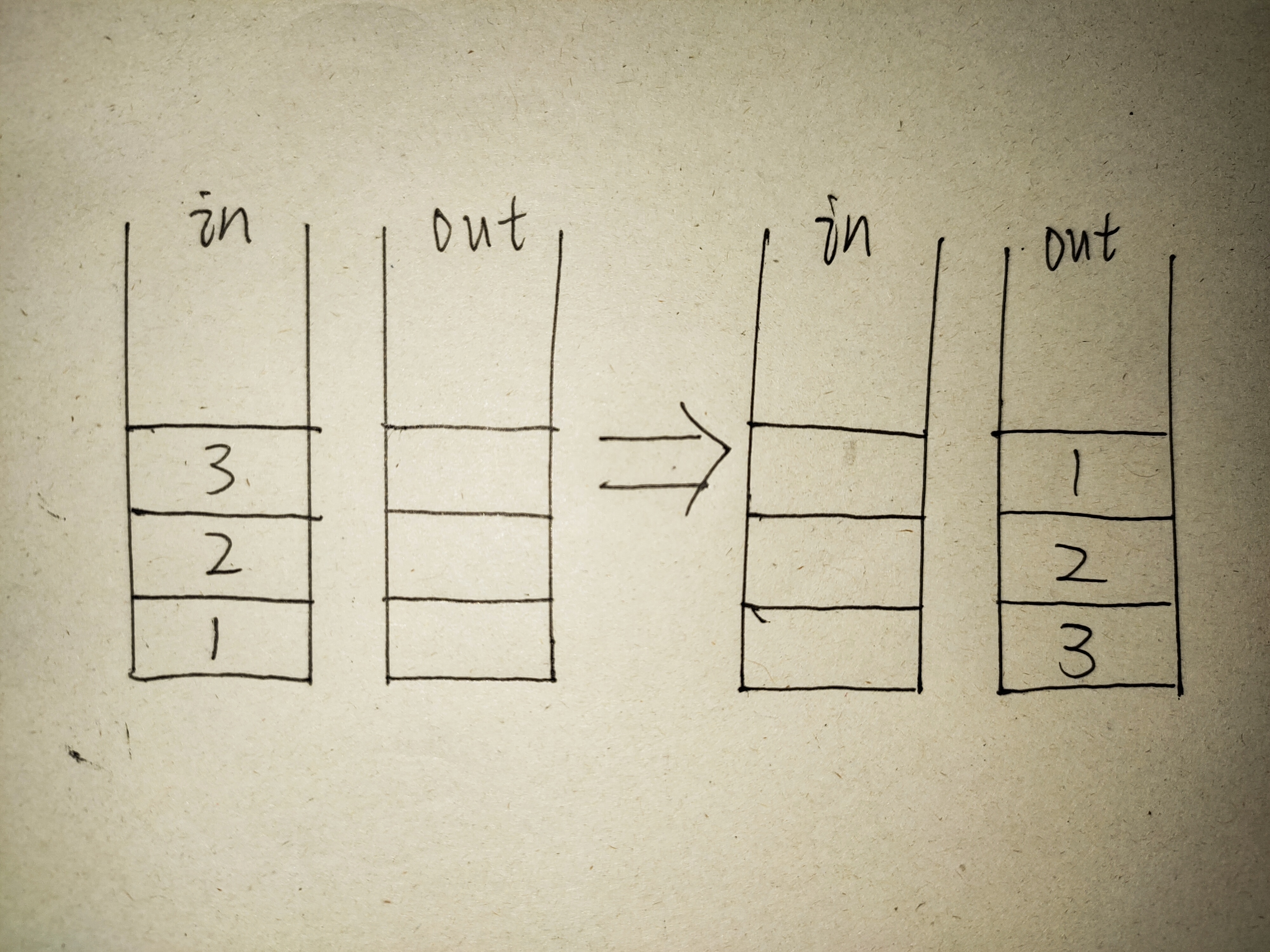
⭐伪代码
class CQueue {
/*创建两个栈*/
创建in栈 //栈in用于存储存入的元素
创建out栈//栈out用于存储用于弹出的元素
public CQueue() {
为栈in开辟空间
为栈out开辟空间
}
public int deleteHead() {
if(两栈都为空) return -1;
if(若栈out中的元素为空)
则将栈in中的元素弹出并存入栈out中
return 弹出元素;
}
}
时间复杂度为O(n)
空间复杂度为O(n)
3.3 分析该题目解题优势及难点。
- 需要深刻的理解栈结构先入后出,以及队列结构先入先出的原理
- 巧妙的运用两个栈结构,将in栈元素弹出到out栈中,实现元素的逆序