Basic Gcd Problem 线性筛

题意

　　给你一个函数，对于每个n和c，求f_c(n)%1e9+7的值。

　　

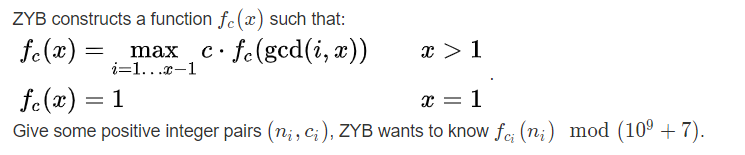
思路

　　我们观察第一个式子，i从1到x-1和x的gcd，求出来的一定就是x的所有因子，一直递归到x=1，我们可以直到答案一定是c的幂，我们要使这个幂尽可能要大。每递归变成一次gcd会使c的幂加一，也就是说递归得越久，答案就越大，于是我们要充分地利用x的质因子，每次只除他的质因子，例如8->4->2->1，递归三次每次除2。

　　综上我们只需要用线性筛处理每个数的质因子个数，输出c的cnt次幂，cnt为n的质因子个数。

AC代码

#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
const int maxn=1e6+5;
const int mod=1e9+7;
typedef long long ll;
int prime[maxn],num[maxn];
bool isprime[maxn];
int t,n,c;
ll ans;
int init(int n)
{
    int cnt=0;
    memset(isprime,true,sizeof(isprime));
    isprime[1]=0;
    for(int i=2;i<=n;i++)
    {
        if(isprime[i]){
            prime[cnt++]=i;
            num[i]=1;
        }
        for(int j=0;j<cnt&&i*prime[j]<=n;j++)
        {
            isprime[i*prime[j]]=0;
            num[i*prime[j]]=num[i]+1;
            if(i%prime[j]==0)
                break;
        }
    }
    return cnt;
}
ll mypow(ll x,ll n,ll p){
    ll res=1;
    while(n){
        if(n&1)
            res=res*x%p;
        x=x*x%p;
        n>>=1;
    }
    return res;
}
int main()
{
    init(maxn);
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&c);
        ans=mypow(c,num[n],mod);
        printf("%d
",ans);
    }
    return 0;
}