卢卡斯定理详解

简述

　　卢卡斯定理是用于求c(n,m) mod p，p为素数的值。
　　题目中求n和m很大的组合数时，结果一般都会溢出，所以经常会求组合数%p的某个值。当p大于m时，我们可以直接根据定义求分母在模p意义下的乘法逆元求出结果：

　　

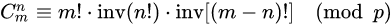
　　但当p<m时，分母的乘法逆元可能不存在(m可能是p的倍数)，所以就轮到卢卡斯定理出场了。

定理描述

　　对于非负整数n，m和质数p

　　

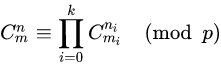
　　其中，为n和m的p进制展开。

　　在做题中我们用到的是递推式：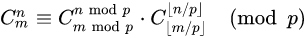

　　当m<n时，规定c(n,m)=0。

证明

　　设x是任意小于p的正整数，那么有：

　　　　

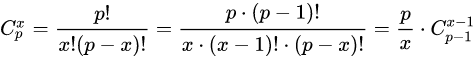
　　因为x<p，所以x存在modp意义下的逆元，于是乎：

　　　　

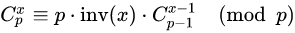
　　因为等式右边是p的倍数，所以：

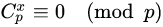　　　　   公式1

---

 　　根据二项式定理，在modp意义下，我们有

　　　　

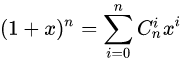
　　当n=p时，根据公式1，除了i=0和i=p时，其余项都为0，所以

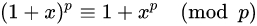
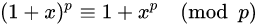　　　　 公式2

---

　　现在我们设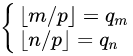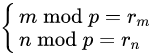，，那么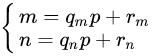

　　根据二项式定理，我们有：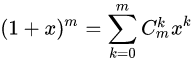

　　我们对等式左端进行变形：

　　

　　也就是说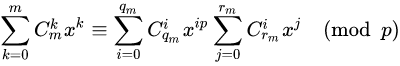

　　我们来看k=n的情况，观察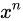项，左边为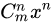，我们现在来看右边，因为j<rm<p，同时rn<rm，我们只能取j=rn，i=qn

　　于是乎我们可以得到：

　　

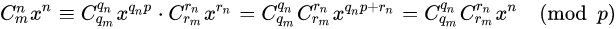
　　两边同时乘inv(xⁿ)，我们就可以得到：

　　

代码详解

　　根据上面的递推式，我们可以写出如下代码：　　

　　注意这里是n下m上，递归终点为m==0

ll lucas(ll n,ll m){
    if(m==0) return 1;
    return lucas(n/p,m/p)*c(n%p,m%p)%p;
}

　　那怎么算C(n,m)呢？我们就要用到乘法逆元，根据定义来算

　　这里的num[i]为i的阶层，inv(i)为i在模p意义下的乘法逆元

ll c(ll n,ll m){
    if(m>n) return 0;
    return (num[n]*inv(num[m])%p)*inv(num[n-m])%p;
}

　　乘法逆元我们用费马小定理来算，这里不展开叙述

ll mypow(ll x,ll n,ll m){
    ll res=1;
    while(n){
        if(n&1) res=res*x%m;
        x=x*x%m;
        n>>=1;
    }
    return res;
}
ll inv(ll x){
    return mypow(x,p-2,p);
}

模板

ll num[maxn];
ll mypow(ll x,ll n,ll m){
    ll res=1;
    while(n){
        if(n&1) res=res*x%m;
        x=x*x%m;
        n>>=1;
    }
    return res;
}
ll inv(ll x){
    return mypow(x,p-2,p);
}
ll c(int n,int m){
    if(m>n) return 0;
    return (num[n]*inv(num[m])%p)*inv(num[n-m])%p;
}
ll lucas(ll n,ll m){
    if(m==0) return 1;
    return lucas(n/p,m/p)*c(n%p,m%p)%p;
}