可持久化线段树

可持久化线段树

什么是可持久化线段树？

即主席树，可以维护区间的第k大，听说可以维护动态区间第k大，也可以维护静态区间第k大，但是我太菜了！只会静态区间第k大。

为什么要叫主席树？听说是某个大佬发明的，只是因为他不懂划分树，然后就发明了这种树，因为跟某主席同名，所以被叫做了主席树，ORZ。

其实，我觉得可持久化线段树的原理跟前缀和的思想是差不多的，前缀和就是一个状态一个状态的进行保留，那么如果线段树的每个状态都得到了保留，那么我们是可以举出任何两个状态之间的线段树，就可以搞定区间第k大的询问了！

那么我们要先了解一个东西，比如单棵线段树如何求区间第k大？每个底层节点代表1，2，3，4，……..，代表第一小，第二小，第三小 ………..，其中节点的sum值代表这个值的出现次数，那么我们只要从根节点出发，判断左节点的sum 是否小于 k，如果是小于的话，那么第k大肯定在右节点里面，如果是大于的话那么第k大肯定是在右节点里面，只要往右边跑就对了，只时候k = k - 右子树的sum，再往下跑，直到找到符合的节点，即第k小。

讲完了这个东西，那我们应该来看一个东西，即如何将单棵线段树，合并起来，你可能会说单棵线段树，一棵一棵保留起来，这样就可以了。。。。。但是我们要先考虑一下，这样去建可持久化线段树肯定是会MLE的。所以我们要考虑一下如何优化空间使得线段树可以放得下，其实我们可以发现每次线段树的更新，只会更新一条路，那么我们只要把这条路保留起来就可以了，就是把这个状态保留起来就OK了。其他的不更新的树，连接到原来的前一棵树就OK了。

如图：

 

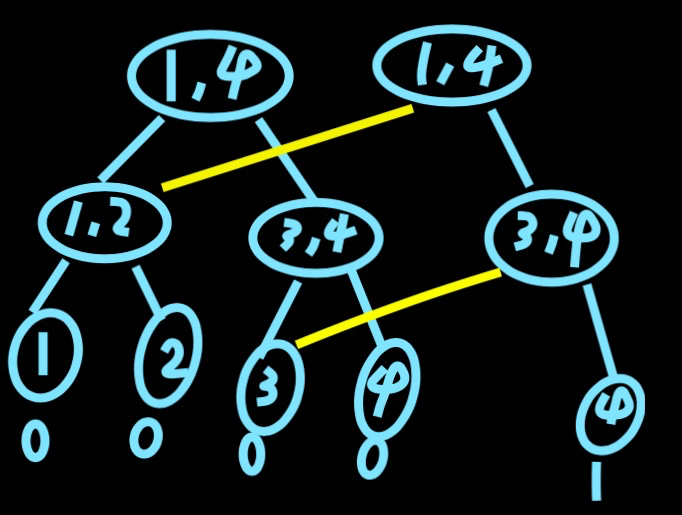
那么我们要如何进行查询操作呢？

我们只要将两棵线段树的状态进行相减就可以得到一个符合的状态的线段树，

就变成了单棵线段树进行查询第k大！

附上代码 例题poj 2104

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
vector<int>vec;
const int MAXN = 100005;
int arr[MAXN];
int root[MAXN];///该数组储存根节点的位置
typedef struct NODE
{
    int l, r, sum;
    /**
     现在的l r 已经不再是单纯的rt << 1 , rt << 1 | 1
     而是指向，指向节点
     **/
}node;
node segtree[MAXN * 20];
int gets(int x)
{
    return lower_bound(vec.begin(), vec.end(), x) - vec.begin() + 1;
}
int tot;
int build(int l, int r)///return p p的值是点的坐标
{
    int p = ++tot;
    segtree[p].sum = 0;
    if(l == r)
    {
        /**
         一层一层的返回就对了。。。。。。
         返回这个节点的坐标就对了。。。。。
         然后才能实现 l r 的指向
         **/
        return p;///返回指向
    }
    int mid = (l + r) >> 1;
    segtree[p].l = build(l, mid);
    segtree[p].r = build(mid + 1, r);
    return p;
}
int update(int now, int l, int r, int pos, int val)
/**
 now - 当前节点 pos - 指要更新的点 val - 权值
 每次更新，都会创建一条链，所以得更新tot
 **/
{
    int p = ++ tot;
    segtree[p] = segtree[now];///这样会将上一个的点
    ///的值赋值给当前的点，这样不需要修改的那棵子树的连接
    ///这样每次多生成的一颗线段树，只要多一条链，所以节省了空间
    if(l == r)
    {
        segtree[p].sum += val;///如果每次更新到底的话，那么就更新底的值
        return p;
    }
    int mid = (l + r) >> 1;
    if(pos <= mid)///如果增加的点 < mid 那么肯定可以往左子树移动
    {
        segtree[p].l = update(segtree[p].l, l, mid, pos, val);
    }
    else///否则向右子树移动
    {
        segtree[p].r = update(segtree[p].r, mid + 1, r, pos, val);
    }
    segtree[p].sum = segtree[segtree[p].l].sum + segtree[segtree[p].r].sum;
    return p;
}
int query(int p, int q, int l, int r, int k)
{
    if(l == r)
        return l;///查询到底就输出
    int mid = (l + r) >> 1;
    int cnt = segtree[segtree[p].l].sum - segtree[segtree[q].l].sum;
    ///将两棵树相减，可得要的状态
    if(k <= cnt)///k 即为第k小，那么就是查询第k小，判断个数再进行移动
    {
        return query(segtree[p].l, segtree[q].l, l, mid, k);
    }
    else
    {
        return query(segtree[p].r, segtree[q].r, mid + 1, r, k - cnt);
    }
}
int main()
{
    int n,q;
    while(~scanf("%d%d",&n,&q))
    {
        memset(arr, 0, sizeof(arr));
        vec.clear();
        tot = 0;
        for (int i = 1; i <= n; i ++) {
            scanf("%d",&arr[i]);
            vec.push_back(arr[i]);
        }
        sort(vec.begin(), vec.end());
        vec.erase(unique(vec.begin(),vec.end()),vec.end());
        ///排序去重，离散处理
        root[0] = build(1, n);
        ///printf("tot = %d
",tot);
        ///先建树
        for (int i = 1; i <= n; i ++) {
            root[i] = update(root[i - 1], 1, n, gets(arr[i]), 1);
        }
        int a, b, c;
        for (int i = 0; i < q; i ++) {
            scanf("%d%d%d",&a,&b,&c);
            int re = query(root[b], root[a - 1], 1, n, c);
            //printf("re = %d
",re);
            printf("%d
",vec[re - 1]);
        }
    }
    return 0;
}