神经网络计算异或

首先介绍“和”操作

x₁, x₂ ∈ {0, 1}

y = x₁ AND x₂

有

[{h_ heta }left( x ight) = gleft( { - 30 + 20{x_1} + 20{x_2}} ight)]

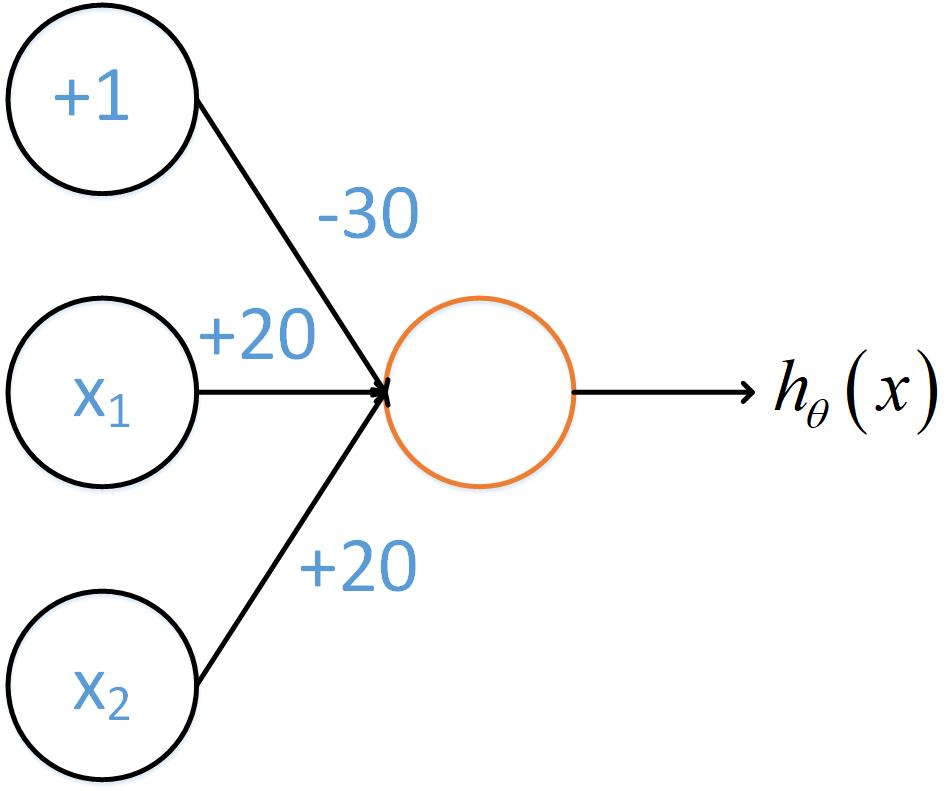
其中g()是sigmoid函数，其图示如下

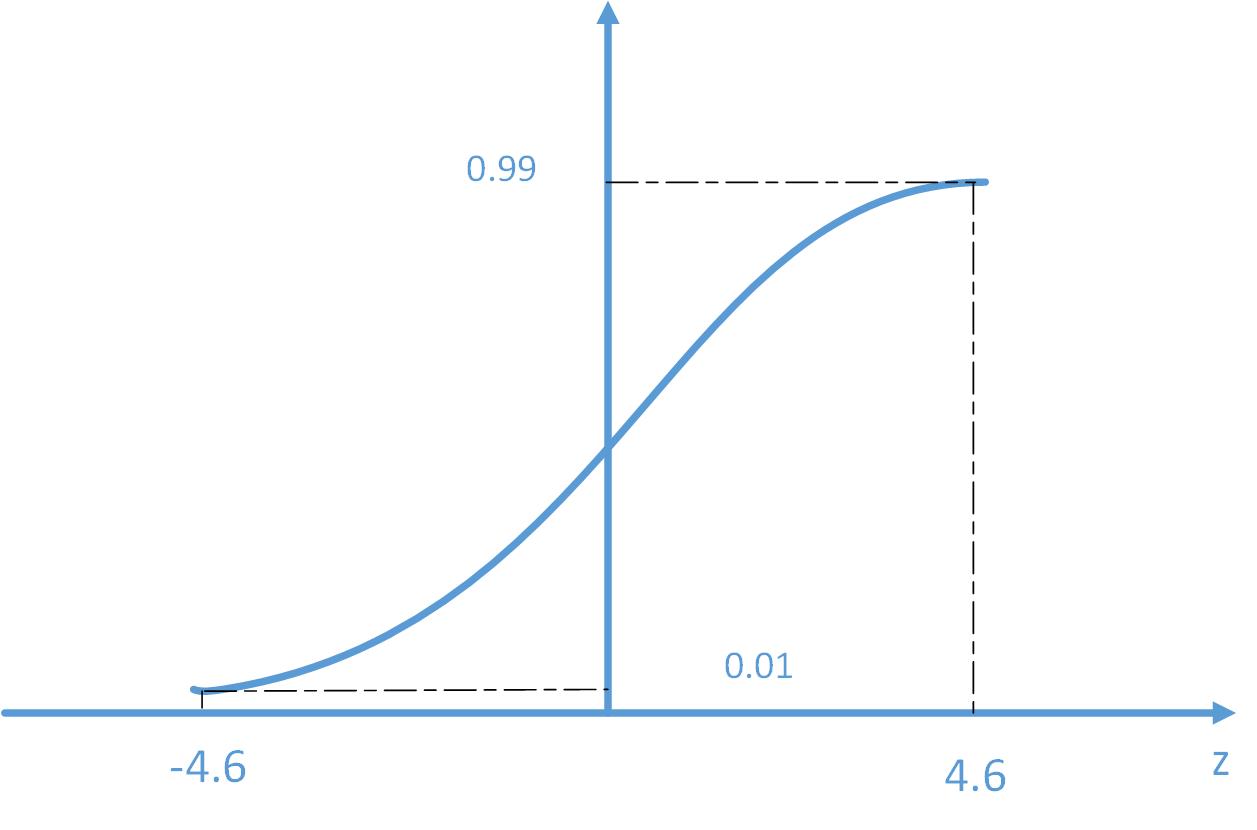
当z=4.6时，函数值约为0.99；当z=-4.6时，函数值约为0.01

计算

x1	x2	h(x)
0	0	g(-30)≈0
0	1	g(-10)≈0
1	0	g(-10)≈0
1	1	g(10)≈1

然后是“或”操作

有

[{h_ heta }left( x ight) = gleft( { - 10 + 20{x_1} + 20{x_2}} ight)]

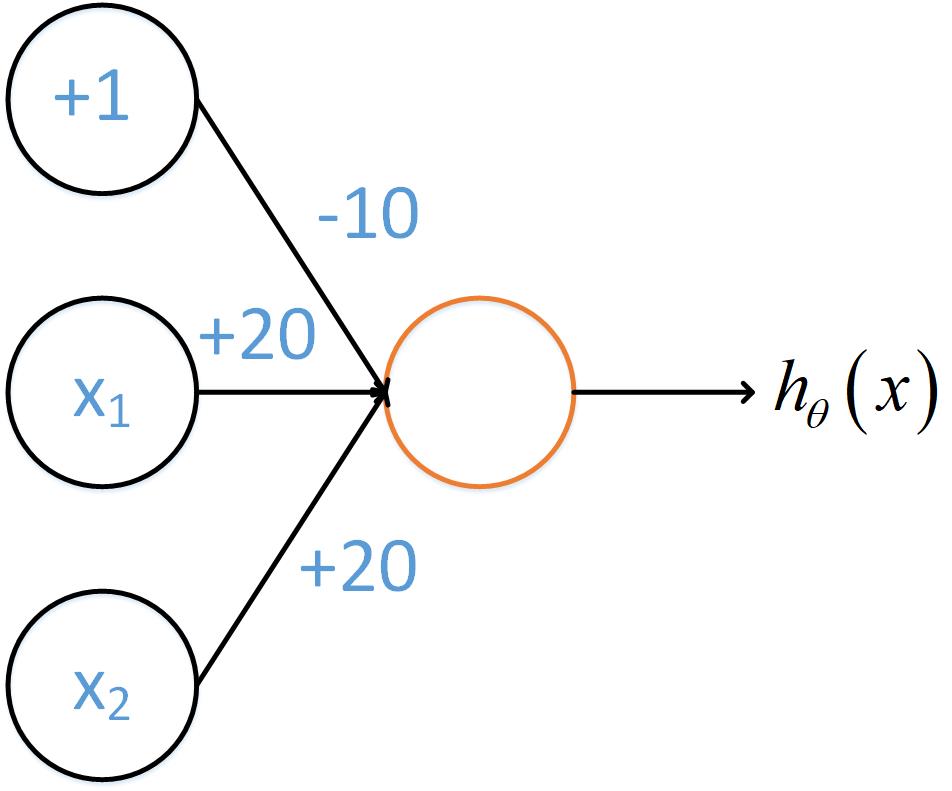
x1	x2	h(x)
0	0	0
0	1	1
1	0	1
1	1	1

然后是“非”操作

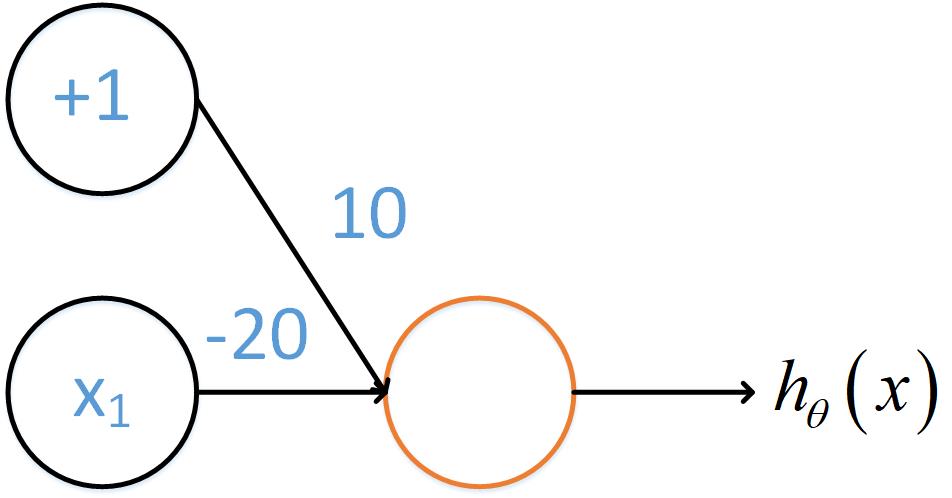
有

[{h_ heta }left( x ight) = gleft( {10 - 20{x_1}} ight)]

计算

x1	h(x)
0	1
1	0

那么“非x1和非x2”如下图

---

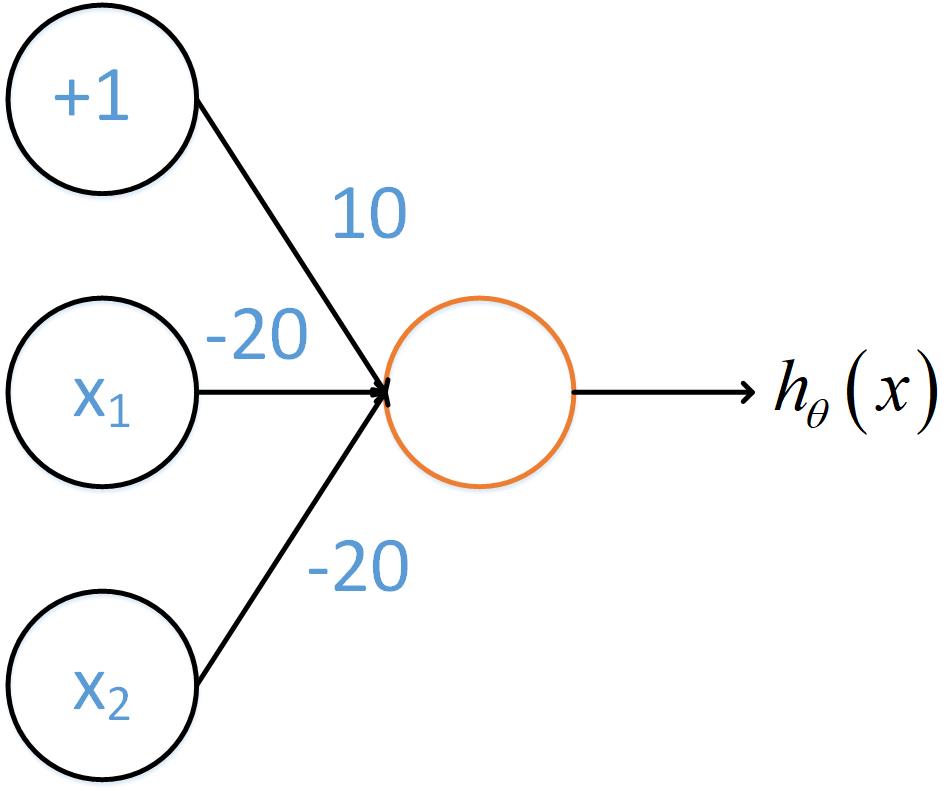
最后计算“异或”

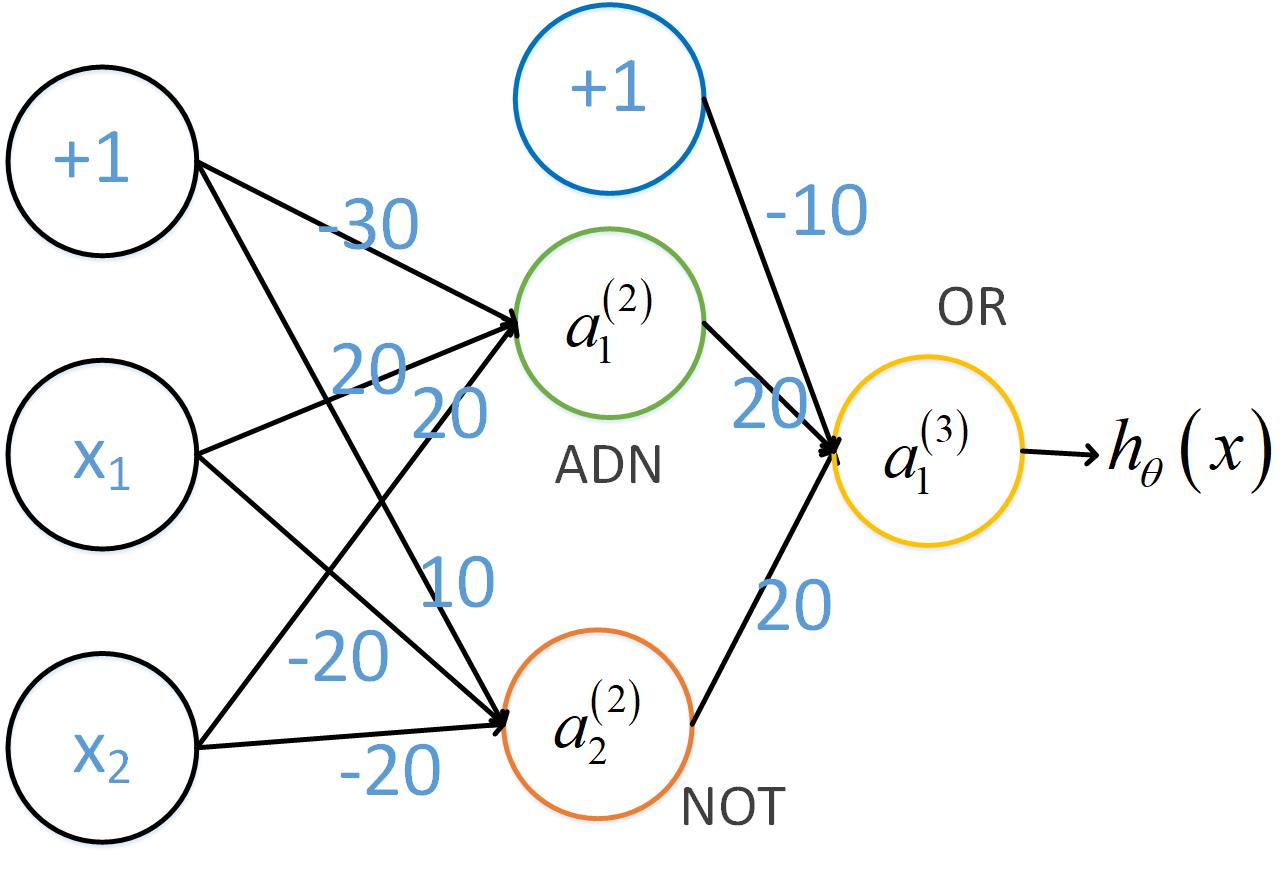
计算

x1	x2	a1(2)	a2(2)	hθ(x)
0	0	0	1	1
0	1	0	0	0
1	0	0	0	0
1	1	1	0	1