最大权独立集问题

题意

给出 \(n\) 个点的二叉树，一次删边的代价是两个点的点权和，并交换两个点，求将所有边都删除的最小花费。

dp

这题的关键就在于：巧妙的 dp 方程。

• 方程定义：

  令 \(u, v\) 表示两个节点，\(y = \text{lca}(u, v)\)，\(d_u\) 表示点 \(u\) 的权值，\(x\) 是 \(y\) 的父亲, 它还未确定。

  \(f_{u, v}\) 表示在 \(y\) 的子树中，将 \(x\) 移到 \(v\) 原来所在位置，并且将 \(u\) 移到 \(x\) 原来所在位置，将所有子树所有边和 \((x, y)\) 断掉的最小花费，(不包含 \(x\) 的产生贡献)。

  理解：感觉和函数差不多，将结点 \(x\) 放入子树内某个位置，返回另一个节点 \(u\)。

  • 用 \(a \to b\) 表示: 将 \(a\) 移到原来 \(b\) 所在位置。

• 转移：

  图的顺序是红到绿到蓝。

  二叉树儿子个数最大是 \(2\), 就按照儿子个数分类讨论。

  令 \(r\) 为当且节点，\(x\) 是 \(r\) 待定的父亲， \(\text{sz}\) 为儿子个数。

  • \(\text{sz} = 0\)

    叶子节点的话，当且仅当

    \[f_{r, r} = d_r \]

    解释：只能将 \(x\) 放入 \(r\) 所在的位置，并且将 \(r\) 移到 \(x\) 所在为值。

    这个就不画了吧。

  • \(\text{sz} = 1\)

    只有一个儿子 \(v_1\)的话，考虑 \(f_{u, v}\)，并且 \(\text{lca}(u, v) = r\) 的话，其中一个必然是 \(r\)。

    1. \(u = r\)

       需要满足 \(x \to v\), \(r \to x\)。

       操作：第一步必须交换 \(x, u\)，剩下就在儿子 \(v_1\) 所在子树找个最小代价的点 \(w\) 移出来，并把 \(x \to v\)。

       \[f_{u, v} = \min_{w} \{ d_u + f_{w, v}\}(\text{lca}(w, v) = v_1) \]

       枚举 \(v, w\) 在 \(O(n^2)\) 内转移即可。

       

    2. \(v = r\)

       需要满足 \(x \to r\), \(u \to x\)。

       操作：在 \(v_1\) 的子树中，枚举交换的方案，需要将 \(u\) 交换到 \(v_1\) 的位置，然后交换 \(r, u\)，再交换 \(u, x\)。

       \[f_{u, v} = \min_{w} \{ f_{u, w} + d_u + d_v \times (\text{dep}_w - \text{dep}_v)\}(\text{lca}(u, w) = v_1) \]

       注意: 这里 \(v(r) \to w\) 的贡献是确定的，因此要算入方案里。

       枚举 \(u, w\), 在 \(O(n^2)\) 内转移即可。

       

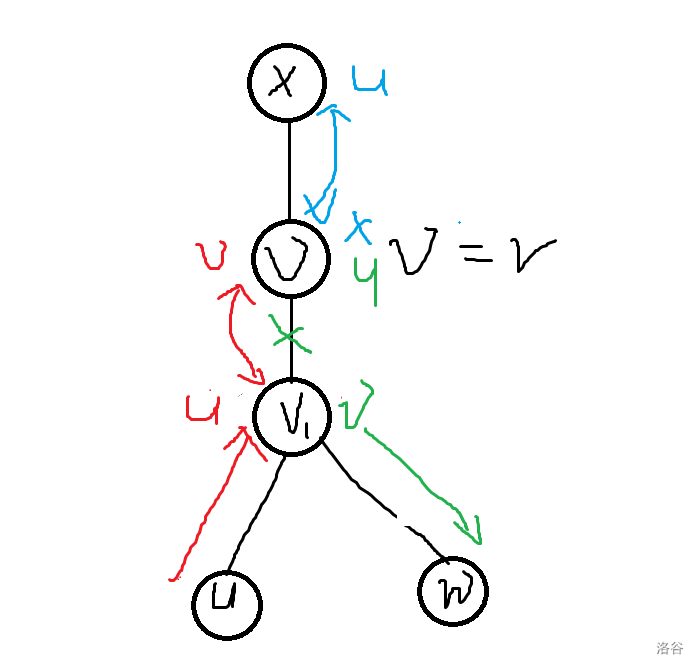
  • \(\text{sz} = 2\)

    有两个儿子 \(v_1, v_2\)。

    仍然是考虑 \(f_{u, v}\) 并且 \(\text{lca}(u, v) = r\)。

    1. \(u = r\)

       要把 \(u(r)\) 移到 \(x\), 必须首先交换\(u, x\), 不然换进子树就回不来了。然后 \(x \to v\)，然后找个最小的方案解决剩下的边。

       \[f_{u, v} = \min_{a,b,w}\{d_u + f_{w,v} + d_w \times(\text{dep}_b -\text{dep}_u) + f_{a, b}\}(\text{lca}(a, b) = v_2, \text{lca}(v, w) = v_1) \]

       \(v_1, v_2\) 在这里仅表示不同的儿子。

       似乎要枚举 \(v, a, b, w\) 转移，实际上, 需要同时枚举的只有 \(a, b\) 、 \(b, w\) 和 \(w, v\)。

       于是可以先枚举 \(a, b\)，只变成与 \(b\) 有关，再枚举 \(b, v\) 只变得与 \(v\) 有关，以此类推。

       都能在 \(O(n^2)\) 完成。
       

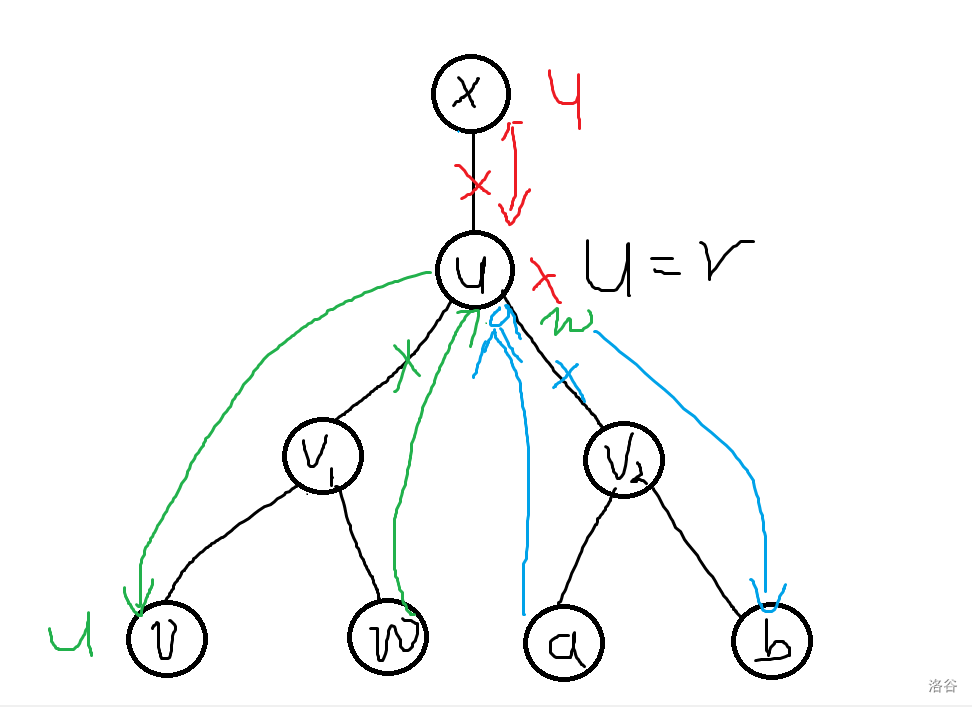
    2. \(v = r\)

       先把 \(u\) 不在的子树全部边断完，再把 \(u\) 所在子树断完，现在 \(u\) 在原来 \(v(r)\) 位置上, 最后再交换 \(u, x\)。

       \[f_{u, v} = \min _{a,b,w} \{ f_{a, b} + d_v \times (\text{dep}_b - \text{dep}_v) + f_{u, w} + d_a \times (\text{dep}_w - \text{dep}_v) + d_u\}(\text{lca}(a, b) = v_1, \text{lca}(u, w) = v_2) \]

       枚举 \(u, a, b, w\)， 和上面一样，同时有关的有 \(u, w\)、\(a, b\) 和 \(a, w\)。

       都在 \(O(n^2)\) 内完成。

       

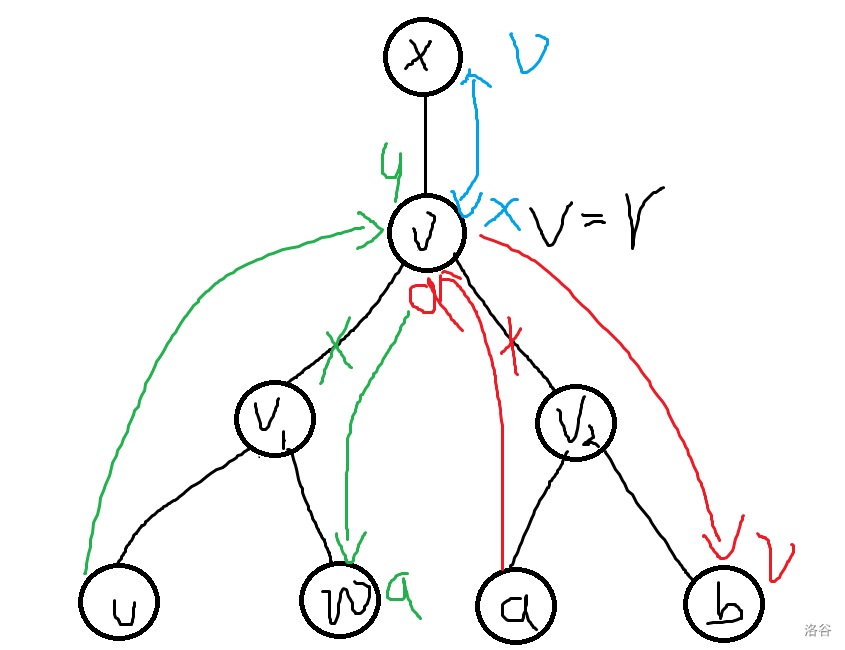
    3. \(u \neq r, v \neq r\)

       先 \(u \to r\), 交换 \(u, x\), 再 \(x \to v\)。

       \[f_{u, v} = \min_{w, a} \{ f_{u, w} + d_r \times (\text{dep}_w - \text{dep}_r) + d_u + f_{a, v} \}(\text{lca}(u, w) = v_1, \text{lca}(a, v) = v_2) \]

       枚举 \(u, w, a, v\), 同时有关 \(u, w\)、 \(a, v\)和 \(u, v\)。

       \(O(n^2)\) 内完成转移。

       

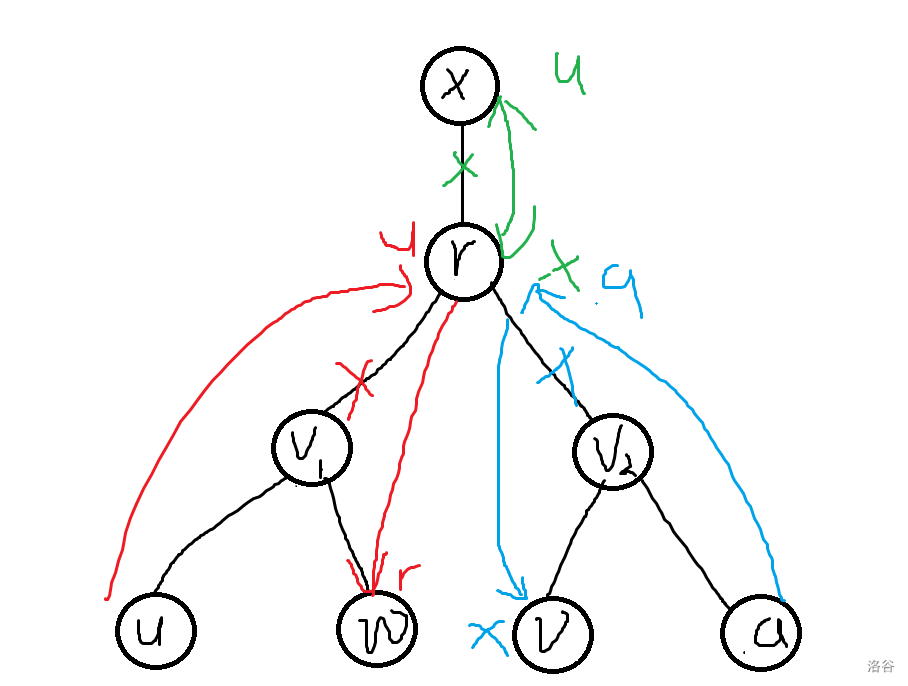
• 求最终答案

  当 \(r = 1\) 时，就不做上面的转移，因为 \(1\) 没有父亲。(其实做了也没事，后三个点超时而已。)

  也按儿子个数分类

  • \(\text{sz} = 1\)
  \[\text{ans} = \min_{u, v} \{f_{u, v} + d_1 \times (\text{dep}_v - \text{dep}_1) \} (\text{lca}(u, v) = v_1) \]

  枚举所有 \(u, v\)， \(O(n^2)\) 即可。

  • \(\text{sz} = 2\)

    \[\text{ans}= \min_{u, v, a, b} \{ f_{u, v} + d_1 \times (\text{dep}_v - \text{dep}_1) + f_{a, b} + d_u \times (\text{dep}_b - \text{dep}_1)\}(\text{lca}(u, v) = v_1, \text{lca}(a, b) = v_2) \]

    枚举 \(u, v, a, b\), 同时有关 \(u, v\)、 \(a, b\) 和 \(u, b\)。

    \(O(n^2)\) 即可。

注意事项：

1. 不开 long long 见祖宗。

2. 枚举形如 \(\text{lca}(u, v) = d\) 的无序对 \((u, v)\) 时，枚举的范围是子树，不然最后总体时间复杂度是 \(O(n^3)\), 和树形背包的时间复杂度一样，合理利用宏定义。

3. 注意转移时的所有点用的都是原来的位置。

代码

暴力转移 (20'):

int n; 
int d[MAXN]; 
int idx; 
int dfn[MAXN], dep[MAXN];  
int L[MAXN], R[MAXN], ls[MAXN], rs[MAXN]; 
ll f[MAXN][MAXN]; 

vector<int> e[MAXN]; 

void getpath(int d, vector<pair<int, int>> &v) {
	v.clear(); 
	v.emplace_back(d, d); 
	int l = ls[d], r = rs[d]; 
	for (int i = L[l]; i <= R[l]; i ++)
		for (int j = L[r]; j <= R[r]; j ++)
			v.emplace_back(dfn[i], dfn[j]), 
			v.emplace_back(dfn[j], dfn[i]); 
	for (int i = L[d] + 1; i <= R[d]; i ++)
		v.emplace_back(d, dfn[i]), 
		v.emplace_back(dfn[i], d); 
} 
int lca[MAXN][MAXN]; 

void dfs(int r) {
	dfn[++ idx] = r; 
	L[r] = idx; 
	for (int v : e[r]) {
		dep[v] = dep[r] + 1; 
		dfs(v); 
	}
	R[r] = idx; 

	int siz = e[r].size(); 
	if (siz == 0) {
		f[r][r] = d[r]; 
		ls[r] = rs[r] = 0; 
	}
	if (siz == 1) {
		int v1 = e[r][0]; 
		ls[r] = v1; rs[r] = 0; 
	}
	if (siz == 2) {
		int v1 = e[r][0], v2 = e[r][1]; 
		ls[r] = v1, rs[r] = v2; 
	}	
	vector<pair<int, int>> path;
	getpath(r, path); 
	for (auto x : path) {
		int u = x.first, v = x.second; 
		assert(lca[u][v] == 0); 
		lca[u][v] = r; 
	}
	if (siz == 1) {
		int u = r, D = e[u][0]; 
		for (int v = 1; v <= n; v ++)
			for (int w = 1; w <= n; w ++)
				if (lca[v][w] == D)
					f[u][v] = min(f[u][v], d[u] + f[w][v]); 
		int v = r; 
		for (int u = 1; u <= n; u ++)
			for (int w = 1; w <= n; w ++)
				if (lca[u][w] == D)
					f[u][v] = min(f[u][v], f[u][w] + d[u] + 1ll * d[v] * (dep[w] - dep[v])); 
	}
	if (siz == 2) {
		int v1 = e[r][0], v2 = e[r][1]; 
		int u = r; 
		for (int v = 1; v <= n; v ++)	
			if (lca[u][v] == r)
			for (int w = 1; w <= n; w ++)
				for (int a = 1; a <= n; a ++)
					for (int b = 1; b <= n; b ++)
						if ( (lca[v][w] == v1 && lca[a][b] == v2) ||
							(lca[v][w] == v2 && lca[a][b] == v1)) 
								f[u][v] = min(f[u][v], d[u] + f[w][v] + f[a][b] + 1ll * d[w] * (dep[b] - dep[u])); 
		
		int v = r; 
		for (int u = 1; u <= n; u ++)
			if (lca[u][v] == r)	
			for (int w = 1; w <= n; w ++) 
				for (int a = 1; a <= n; a ++)
					for (int b = 1; b <= n; b ++)
						if ( (lca[u][w] == v1 && lca[a][b] == v2) ||
							(lca[u][w] == v2 && lca[a][b] == v1)) 
								f[u][v] = min(f[u][v], f[a][b] + 1ll * d[v] * (dep[b] - dep[v]) + f[u][w] + 1ll * d[a] * (dep[w] - dep[v]) + d[u]); 						
		
		for (int u = 1; u <= n; u ++)	
			for (int v = 1; v <= n; v ++)
				if (lca[u][v] == r)
				for (int w = 1; w <= n; w ++)
					for (int a = 1; a <= n; a ++)
						if ( (lca[u][w] == v1 && lca[a][v] == v2) ||
							(lca[u][w] == v2 && lca[a][v] == v1))
								f[u][v] = min(f[u][v], f[u][w] + 1ll * d[r] * (dep[w] - dep[r]) + f[a][v] + d[u]);  
	}
}

int main() {
	ios::sync_with_stdio(false); 
	cin.tie(0); cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i ++)
		cin >> d[i]; 
	for (int i = 2, c; i <= n; i ++) {
		cin >> c; 
		e[c].emplace_back(i); 
	}
	memset(f, 0x3f, sizeof(f)); 
	L[0] = 0, R[0] = -1; 
	dfs(1); 
	ll ans = INF;
	int sz = e[1].size(); 
	if (sz == 1) {
		int v = ls[1]; 
		for (int a = 1; a <= n; a ++)
			for (int b = 1; b <= n; b ++)
				if (lca[a][b] == v) 
					ans = min(ans, f[a][b] + 1ll * d[1] * dep[b]); 
	}
	if (sz == 2) {
		int v1 = ls[1], v2 = rs[1]; 
		for (int a = 1; a <= n; a ++)
			for (int b = 1; b <= n; b ++)
				for (int u = 1; u <= n; u ++)
					for (int v = 1; v <= n; v ++)
						if ( (lca[a][b] == v1 && lca[u][v] == v2) ||
							(lca[a][b] == v2 && lca[u][v] == v1))
								ans = min(ans, f[a][b] + 1ll * d[1] * dep[b] + f[u][v] + 1ll * d[a] * dep[v]); 
	}
	cout << ans << endl;  
	return 0; 
}

AC代码:

#include<bits/stdc++.h>
using namespace std;

using ll = long long; 
const int MAXN = 5010; 
const ll INF = 1e14;

int n; 
int d[MAXN]; 
int idx; 
int dfn[MAXN], dep[MAXN];  
int L[MAXN], R[MAXN], ls[MAXN], rs[MAXN]; 
ll f[MAXN][MAXN], g[MAXN], h[MAXN]; 

vector<int> e[MAXN]; 


int lca[MAXN][MAXN]; 

#define forlca1(u, v, d) \
		for (int _i = L[ls[d]], u; u = dfn[_i], _i <= R[ls[d]]; _i ++) \
			for (int _j = L[rs[d]], v; v = dfn[_j], _j <= R[rs[d]]; _j ++) 
#define forlca2(u, v, d) \
		for (int _i = L[rs[d]], u; u = dfn[_i], _i <= R[rs[d]]; _i ++) \
			for (int _j = L[ls[d]], v; v = dfn[_j], _j <= R[ls[d]]; _j ++) 
#define forlca3(u, v, d) \
		for (int _i = L[d], u = d, v; v = dfn[_i], _i <= R[d]; _i ++) 	
#define forlca4(u, v, d) \
		for (int _i = L[d], v = d, u; u = dfn[_i], _i <= R[d]; _i ++) 			
	
#define forlca(u, v, d, expr) \
	forlca1(u, v, d) \
		expr \
	forlca2(u, v, d) \
		expr \
	forlca3(u, v, d) \
		expr \
	forlca4(u, v, d) \
		expr 

void dfs(int r) {
	dfn[++ idx] = r; 
	L[r] = idx; 
	for (int v : e[r]) {
		dep[v] = dep[r] + 1; 
		dfs(v); 
	}
	R[r] = idx; 

	int siz = e[r].size(); 
	if (siz == 0) {
		f[r][r] = d[r]; 
		ls[r] = rs[r] = 0; 
	}
	if (siz == 1) {
		int v1 = e[r][0]; 
		ls[r] = v1; rs[r] = 0; 
	}
	if (siz == 2) {
		int v1 = e[r][0], v2 = e[r][1]; 
		ls[r] = v1, rs[r] = v2; 
	}	
	
	if (r == 1) return; 
	int l = ls[r], rr = rs[r]; 
	for (int i = L[l]; i <= R[l]; i ++)
		for (int j = L[rr]; j <= R[rr]; j ++)
			lca[dfn[i]][dfn[j]] = lca[dfn[j]][dfn[i]] = r; 
	for (int i = L[r]; i <= R[r]; i ++)
			lca[dfn[i]][r] = lca[r][dfn[i]] = r; 
	
	if (siz == 1) {
		int u = r, D = e[u][0]; 
		forlca(v, w, D, f[u][v] = min(f[u][v], d[u] + f[w][v]);)
		
		int v = r; 
		forlca(u, w, D, f[u][v] = min(f[u][v], f[u][w] + d[u] + 1ll * d[v] * (dep[w] - dep[v]));) 
	}
	
	if (siz == 2) {
		int v1 = e[r][0], v2 = e[r][1]; 
		int u = r; 
		for (int t = 2; t; t --) {
			for (int b = 1; b <= n; b ++)
				g[b] = INF; 
			forlca(b, a, v2, g[b] = min(g[b], f[a][b]);) 
			for (int w = 1; w <= n; w ++)
				h[w] = INF; 
			forlca(w, b, r, h[w] = min(h[w], 1ll * d[w] * (dep[b] - dep[u]) + g[b]);)
			
			forlca(v, w, v1, (lca[u][v] == r ? f[u][v] = min(f[u][v], d[u] + f[w][v] + h[w]) : 114514);)
			swap(v1, v2); 
		}
		
		
		int v = r; 
		for (int t = 2; t; t --) {
			for (int b = 1; b <= n; b ++)
				g[b] = INF; 
			forlca(b, a, v2, g[a] = min(g[a], f[a][b] + 1ll * d[v] * (dep[b] - dep[v]));)		
			for (int w = 1; w <= n; w ++)
				h[w] = INF; 
			forlca(w, a, r, h[w] = min(h[w], g[a] + 1ll * d[a] * (dep[w] - dep[v]));)
					
			forlca(u, w, v1, (lca[u][v] == r? f[u][v] = min(f[u][v],  h[w] + f[u][w] + d[u]) : 1919810);)
			swap(v1, v2); 
		}
		 						
		for (int t = 2; t; t --) {
			for (int u = 1; u <= n; u ++)
				g[u] = INF; 
			forlca(u, w, v1, g[u] = min(g[u], f[u][w] + 1ll * d[r] * (dep[w] - dep[r]) + d[u]);)
			for (int v = 1; v <= n; v ++)
				h[v] = INF;  
			forlca(v, a, v2, h[v] = min(h[v], f[a][v]);)
					
			forlca(u, v, r, f[u][v] = min(f[u][v],  h[v] + g[u]);)
			swap(v1, v2); 
		}
	
	}
}

int main() {
	ios::sync_with_stdio(false); 
	cin.tie(0); cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i ++)
		cin >> d[i]; 
	for (int i = 2, c; i <= n; i ++) {
		cin >> c; 
		e[c].emplace_back(i); 
	}
	memset(f, 0x3f, sizeof(f)); 
	L[0] = 0, R[0] = -1; 
	dfs(1); 
	ll ans = INF;
	int sz = e[1].size(); 
	if (sz == 1) {
		int v = ls[1]; 
		forlca(a, b, v, ans = min(ans, f[a][b] + 1ll * d[1] * dep[b]);)
	}
	if (sz == 2) {
		int v1 = ls[1], v2 = rs[1]; 
		for (int t = 2; t; t --) {
			for (int a = 1; a <= n; a ++)
				g[a] = INF; 	
			forlca(a, b, v1, g[a] = min(g[a], f[a][b] + 1ll * d[1] * dep[b]);)
			for (int v = 1; v <= n; v ++)
				h[v] = INF;
			forlca(v, a, 1, h[v] = min(h[v], g[a] + 1ll * d[a] * dep[v]);)
			forlca(u, v, v2, ans = min(ans, f[u][v] + h[v]);)
			swap(v1, v2); 
		}
		
	}
	cout << ans << endl;  
	return 0; 
}