迪杰斯特拉

迪杰斯特拉

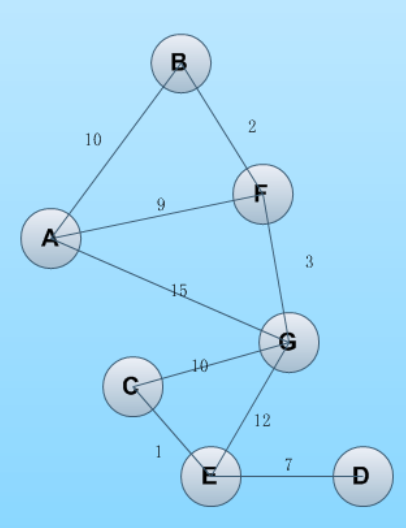
INF_val = 100000 
  
class Dijkstra_Path():  
    def __init__(self, node_map):  
        self.node_map = node_map  
        self.node_length = len(node_map)  
        self.used_node_list = []  
        self.collected_node_dict = {}  
      
    def __call__(self, from_node, to_node):  
        self.from_node = from_node  
        self.to_node = to_node  
        self._init_dijkstra()  
        return self._format_path()  
  
    def _init_dijkstra(self):  
        ## Add from_node to used_node_list  
        self.used_node_list.append(self.from_node)  
        for index1 in range(self.node_length):  
            self.collected_node_dict[index1] = [INF_val, -1]  
    
        self.collected_node_dict[self.from_node] = [0, -1] # from_node don't have pre_node  
        for index1, weight_val in enumerate(self.node_map[self.from_node]):  
            if weight_val:  
                self.collected_node_dict[index1] = [weight_val, self.from_node] # [weight_val, pre_node]  
          
        self._foreach_dijkstra()  
      
    def _foreach_dijkstra(self):  
        while(len(self.used_node_list) < self.node_length - 1):  
            min_key = -1  
            min_val = INF_val  
            for key, val in self.collected_node_dict.items(): # 遍历已有权值节点  
                if val[0] < min_val and key not in self.used_node_list:  
                    min_key = key  
                    min_val = val[0]  
  
            ## 把最小的值加入到used_node_list          
            if min_key != -1:  
                self.used_node_list.append(min_key)  
  
            for index1, weight_val in enumerate(self.node_map[min_key]):  
                ## 对刚加入到used_node_list中的节点的相邻点进行遍历比较  
                if weight_val > 0 and self.collected_node_dict[index1][0] > weight_val + min_val:  
                    self.collected_node_dict[index1][0] = weight_val + min_val # update weight_val  
                    self.collected_node_dict[index1][1] = min_key  
  
  
    def _format_path(self):  
        node_list = []  
        temp_node = self.to_node  
        node_list.append((temp_node, self.collected_node_dict[temp_node][0]))  
        while self.collected_node_dict[temp_node][1] != -1:  
          temp_node = self.collected_node_dict[temp_node][1]  
          node_list.append((temp_node, self.collected_node_dict[temp_node][0]))  
        node_list.reverse()  
        return node_list  
  
def set_node_map(node_map, node, node_list):  
    for x, y, val in node_list:  
        node_map[node.index(x)][node.index(y)] = node_map[node.index(y)][node.index(x)] = val  
  
      
if __name__ == "__main__":  
    node = ['A', 'B', 'C', 'D', 'E', 'F', 'G']   //顶点
    node_list = [('A', 'F', 9), ('A', 'B', 10), ('A', 'G', 15), ('B', 'F', 2),    //点与点间的距离
                 ('G', 'F', 3), ('G', 'E', 12), ('G', 'C', 10), ('C', 'E', 1),  
                 ('E', 'D', 7)]  
    
    ## init node_map to 0  
    node_map = [[0 for val in range(len(node))] for val in range(len(node))]  
    
    ## set node_map  
    set_node_map(node_map, node, node_list)  
    
    ## select one node to obj node, e.g. A --> D(node[0] --> node[3])  
    from_node = node.index('A')  
    to_node = node.index('E')  
    dijkstrapath = Dijkstra_Path(node_map)  
    path = dijkstrapath(from_node, to_node)  
    print(path) 


------------------------------------------------------------------------------

[(0, 0), (5, 9), (6, 12), (2, 22), (4, 23)]         （点，权值）

Floyd算法(Floyd-Warshallalgorithm)又称为弗洛伊德算法

INF_val = 9999

class Floyd_Path():
def __init__(self, node, node_map, path_map):
self.node = node
self.node_map = node_map
self.node_length = len(node_map)
self.path_map = path_map
self._init_Floyd()

def __call__(self, from_node, to_node):
self.from_node = from_node
self.to_node = to_node
return self._format_path()

def _init_Floyd(self):
for k in range(self.node_length):
for i in range(self.node_length):
for j in range(self.node_length):
tmp = self.node_map[i][k] + self.node_map[k][j]
if self.node_map[i][j] > tmp:
self.node_map[i][j] = tmp
self.path_map[i][j] = self.path_map[i][k]

print('_init_Floyd is end')


def _format_path(self):
node_list = []
temp_node = self.from_node
obj_node = self.to_node
print("the shortest path is: %d"%(self.node_map[temp_node][obj_node]))
node_list.append(self.node[temp_node])
while True:
node_list.append(self.node[self.path_map[temp_node][obj_node]])
temp_node = self.path_map[temp_node][obj_node]
if temp_node == obj_node:
break;

return node_list





def set_node_map(node_map, node, node_list, path_map):
for i in range(len(node)):
## 对角线为0
node_map[i][i] = 0
for x, y, val in node_list:
node_map[node.index(x)][node.index(y)] = node_map[node.index(y)][node.index(x)] = val
path_map[node.index(x)][node.index(y)] = node.index(y)
path_map[node.index(y)][node.index(x)] = node.index(x)


if __name__ == "__main__":
node = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
node_list = [('A', 'F', 9), ('A', 'B', 10), ('A', 'G', 15), ('B', 'F', 2),
('G', 'F', 3), ('G', 'E', 12), ('G', 'C', 10), ('C', 'E', 1),
('E', 'D', 7)]

## node_map[i][j] 存储i到j的最短距离
node_map = [[INF_val for val in range(len(node))] for val in range(len(node))]
## path_map[i][j]=j 表示i到j的最短路径是经过顶点j
path_map = [[0 for val in range(len(node))] for val in range(len(node))]

## set node_map
set_node_map(node_map, node, node_list, path_map)


## select one node to obj node, e.g. A --> D(node[0] --> node[3])
from_node = node.index('A')     //起点
to_node = node.index('E') 　　　　//终点 
Floydpath = Floyd_Path(node, node_map, path_map)
path = Floydpath(from_node, to_node)
print(path)

-----------------------------------------------------------------------------------------

_init_Floyd is end
the shortest path is: 23
['A', 'F', 'G', 'C', 'E']