KMP算法是判断一个字符串(模式串)是不是另一个字符串(文本串)的子串的常用算法,其中KMP算法的失配指针的概念(在本算法也叫next数组)在AC自动机中也有突出使用。
朴素的字符串匹配算法
朴素的字符串匹配算法,即判断文本串的以每一个字符为开头,与模式串等长的子字符串是否与模式串本身相等。很明显复杂度为为 O(mn),其中m为文本串的长度,n为模式串的长度。具体实现如下图
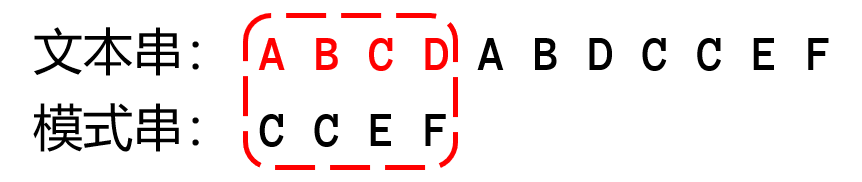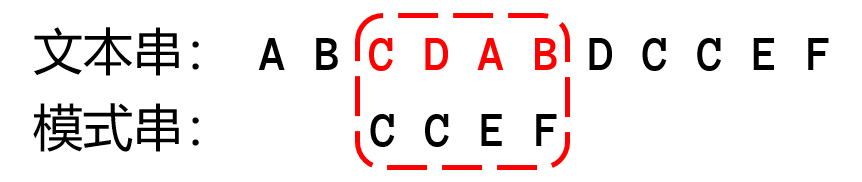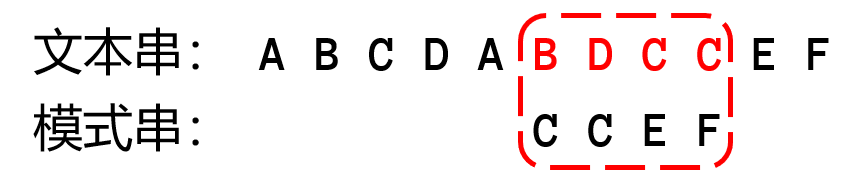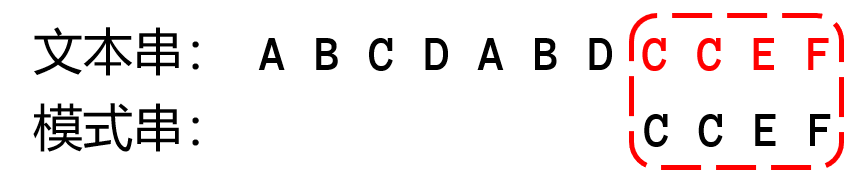
上图是一个字符串朴素匹配的示意图,长度为4的模式串与文本串每一个连续的长度为4的子串进行匹配判断,每一次匹配判断都需要一个个字符比较。
朴素匹配的代码:
int StringMatch(string s, string p){ //s为文本串,p为模式串 int sLen = s.size(); int pLen = p.size(); int i = 0; //i遍历文本串下标,j遍历模式串下标 int j = 0; while (i < sLen && j < pLen){ if (s[i] == p[j]){ //相同i和j一起加1 i++; j++; } else{ i = i - j + 1; //i指向文本串下一个子串的第一个字符。 j = 0; //不相同,j重新指向模式串第一个字符 } } if (j == pLen) return i - j; else return -1; }
具体示例
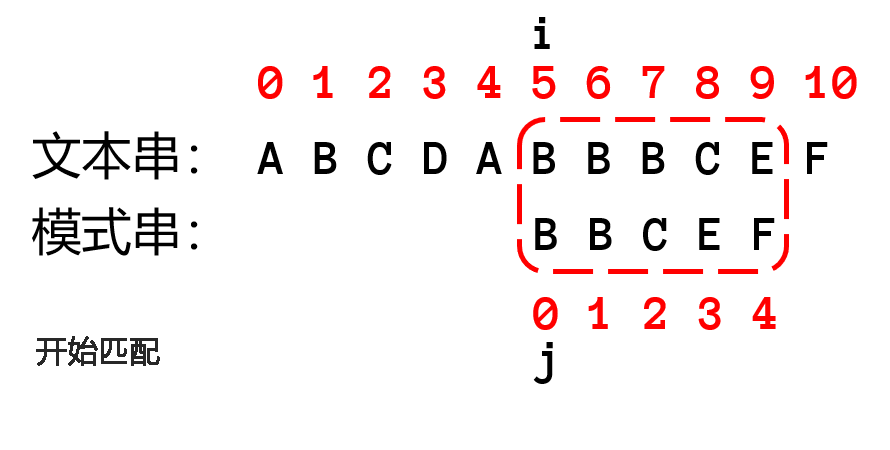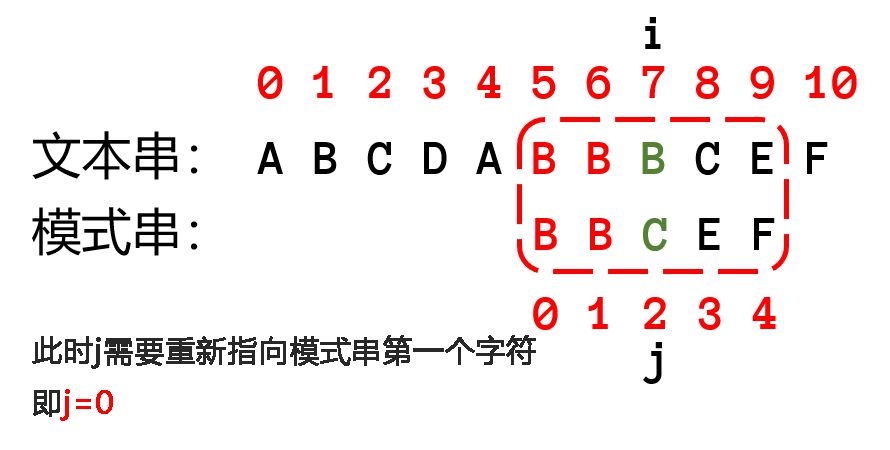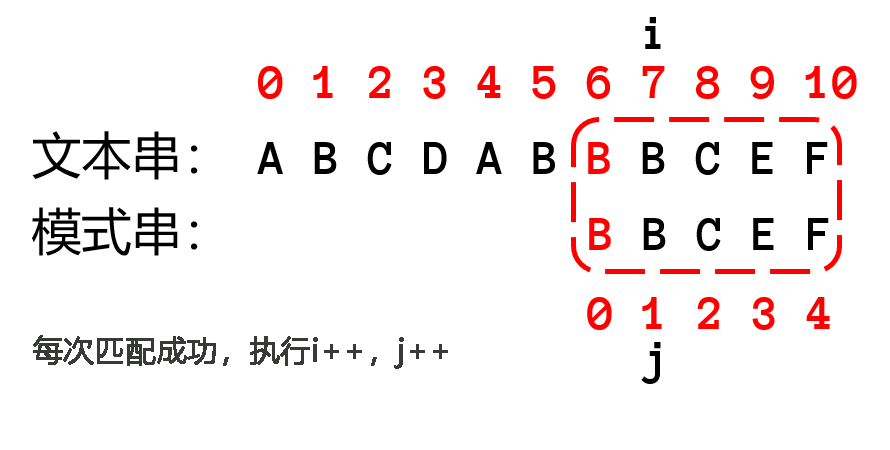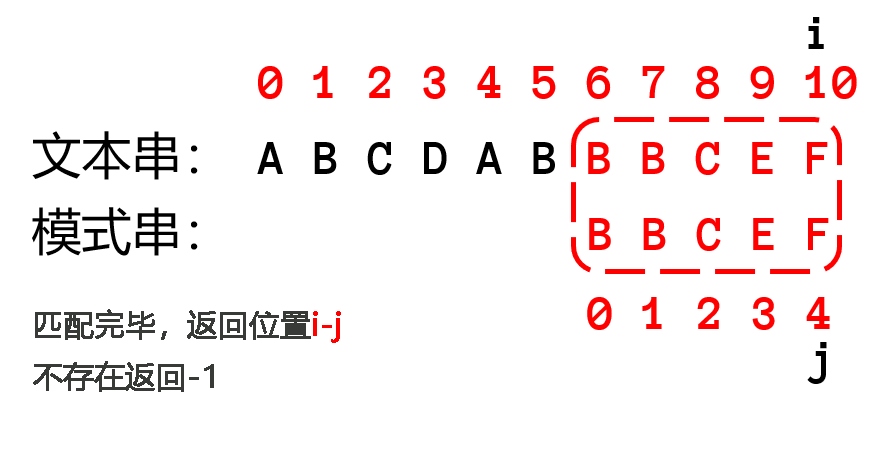
很明显,如果要优化算法,首先要从 while 中的 ifelse 语句中优化(主要优化匹配失败的处理方法),下面可以比较朴素算法(左)和KMP算法的代码差异
int StringMatch(string s, string p){ //s为文本串,p为模式串 int sLen = s.size(); int pLen = p.size(); int i = 0; //i遍历文本串下标,p遍历模式串下标 int j = 0; while (i < sLen && j < pLen){ if (s[i] == p[j]){ i++; j++; } else{ i = i - j + 1; j = 0; } } if (j == pLen) return i - j; else return -1; }
int Next[maxn]; //这个数组是KMP的关键 int KMP(const string &s, const string &p){ //s为文本串,p为模式串 GetNext(p); //获得Next数组,暂时先不用管 int i = 0; //i遍历文本串下标,j遍历模式串下标 int j = 0; int s_len = s.size(); int p_len = p.size(); while(i < s_len && j < p_len){ if(j == -1 || s[i] == p[j]){ i++; j++; } else j = Next[j]; //与暴力不一样的地方 } if(j == p_len)
return i - j; else
return -1; }
KMP算法大致预思维
通过上面的比较,可以得出KMP算法的一个特点:
1.如果 $s[i] == p[j]$,则 $i++,j++$;
2.如果 $s[i] eq p[j]$,则 $j = Next[j]$
那么一定有个疑问,$Next$ 数组是干嘛的?
可以回过头来看上面那个匹配失败的图片
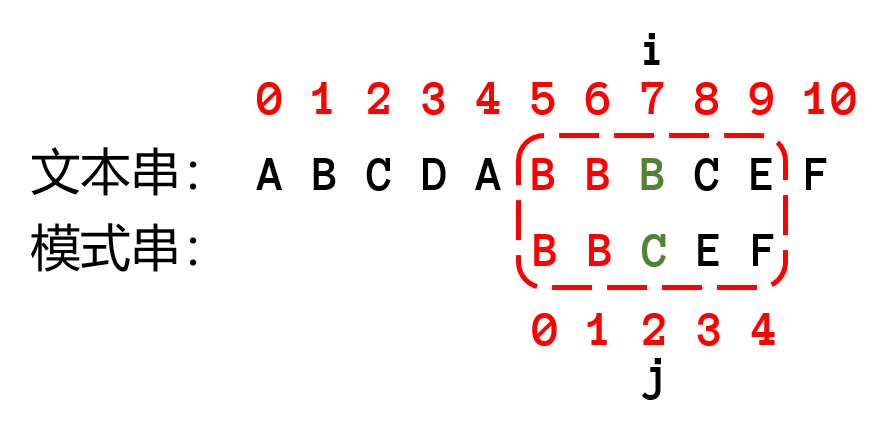
研究匹配失败的操作,可以发现,把模式串已经匹配的字符组成一个子串,上图的子串为 $BB$,这个子串拥有相同的最长前后缀(即字母 $B$),由于这个子串已经匹配成功了,那么说明文本串的已匹配的子串有同样的后缀(即字母 $B$),让模式串已匹配串的前缀与文本串已匹配串的后缀重新匹配。可以移动模式串直到前缀位置与文本串的已匹配子串的后缀位置相等,然后继续一一往后匹配。可以看下图

上面的例子,前后缀只有一个字符,这里在放出一个例子

这种匹配失败的处理方法,并没有移动 $i$,所以KMP算法的复杂度只有 $O(n)$
在写代码过程中,我们只需在意匹配失败,j需要重新指向第几个字符,而不必在意移动模式串,所以 $Next[j]$ 代表着,当在模式串的 $j$ 号位置字符匹配失败后,$j$ 需要指向的新位置。当然前面所举的例子只是存在最长前后缀的情况下,如果前面两个例子稍微懂了一些,可以接下来往后看。再来讨论一下 $Next$ 数组怎么求。
KMP的Next数组求法
在上面的例子中,可以发现Next数组是处理失配操作的核心,且有一个很关键的步骤,就是找模式串已匹配子串的最长相同前后缀,在这里需要说明的是:
所找到的前后缀不能是子串本身,否则没有任何意义。
找到前后缀后,既然前后缀是相同的,而且文本串已匹配的子串(上面例子中标红色的子串即为已匹配子串)与模式串已匹配的子串是相同的,那么文本串已匹配子串的后缀明显可以和模式串已匹配子串的前缀进行匹配。这句话是求得 Next 数组,乃至KMP降低复杂度的核心。
于是 $Next[j]$ 更明显的意义,就是模式串 $j$ 位置之前的前缀子串的最长相同前后缀的长度,从这点可以看出 $Next$ 数组只与模式串有关,如下图所示,红色串为 $j$ 位置之前的前缀子串,标蓝色说明是最长相同前后缀。

注意,对于任意模式串,需要定义 $Next[0] = -1$,表示在模式串第一个字符就匹配失败的话,i和j都是要自加一,在后面的代码中还会讲解,记住这个结论就行。于是上图模式串的 $Next$ 数组为 $left{ -1, 0, 0, 0, 0, 1, 2 ight}$,这也能解释之前的图中,为何在字符 'D' 处失配,$j$ 要指向 2 位置的字符 'C'$(Next[6] = 2)$
看到这里,至少可以对于任何一个子串,在草稿纸上写出它的 $Next$ 数组,但是这是远远不够的,我们需要用代码来实现,我们看看最基本逻辑的得到 $Next$ 数组的代码。
void GetNext(const string &p){ int p_len = p.size(); int i = 0; int j = -1; Next[i] = -1; //Next数组一开始全为0,Next[0]初始化为-1 while(i < p_len){ //求 i 位置之前的前缀子串的最长相同前后缀的长度 if(j == -1 || p[i] == p[j]){ //p[i] 与 p[j] 相同,则都自加1,然后更新Next[i] i++; j++; Next[i] = j; } else{ //失配,j重新指回0,i也重新指向i-j+1的位置 j = 0; i = i - j + 1; } } return; }
仔细一看,是不是特别像暴力字符串匹配的算法代码,那我们是不是可以用同样 $Next$ 数组处理失配的方法来优化 $else$ 内的语句,刚刚好我们现在正在求得就是 $Next$ 数组,我们可以用当前已经求出来的 $Next$ 数组的部分值来反过来优化失配操作来求出剩余的 $Next$ 数组内的值,所以优化后的代码就是把已经求出来的 $Next[j]$ 的值赋给 $j$,同时 $i$ 不变,这和之前讲的失配处理是同样的方式:
void GetNext(const string &p){ int p_len = p.size(); int i = 0; int j = -1; Next[i] = -1; while(i < p_len){ if(j == -1 || p[i] == p[j]){ i++; j++; Next[i] = j; } else j = Next[j]; } return; }
在代码中,$Next$ 数组的初始值都为0,可以看到 $Next[0]$ 被初始化为 $1$,同时还定义了 $j = -1$ 的状态。由于 $Next[0]$ 的值已经知道了,我们只需从 $Next[1]$ 开始求值,但是 $i$ 被初始化为 $0$,所以在循环的 $if$ 条件中,如果 $j == -1$,需要执行 $i++,j++$
下面是求字符串 "ABCDABD" 的 $Next$ 数组的动态动画,可见求 $Next$ 数组的失配操作和字符串匹配的失配操作一样(图动的有点慢,大家稍微忍耐一下)

非常非常非常重要的优化:
用上面的求法,很明显字符串 $P$ 为 "ABABABD" 的 $Next$ 数组为 $left{-1, 0, 0, 1, 2, 3, 4 ight}$
看似没有问题,假设上面字符串为模式串,且在匹配过程中在第三个 $A$ 处失配,那么 $j = Next[j] = 2$,但是发现 $P[2]$ 仍然是 $A$(仍然失配),那么 $j$ 还需往前跳(即 $j = Next[j]$),直到 $j = -1$,如果这条字符串很长,那么 $j$ 需要一直往前跳,直到 $j = -1$,很明显复杂度退化了,为此优化后的代码如下
void GetNext(const string &p){ int p_len = p.size(); int i = 0; int j = -1; Next[i] = -1; while(i < p_len){ if(j == -1 || p[i] == p[j]){ i++; j++; if(p[i] != p[j]) Next[i] = j; else Next[i] = Next[j]; //如果往前跳跃后仍然是相同的字符,那么就等于再次跳跃后的 Next 值 } else j = Next[j]; } return; }
用上面代码的得出字符串 "ABABABD" 的 $Next$ 数组为 $left{-1, 0, -1, 0, -1, 0, 4 ight}$,很优秀的解决了这个问题。
当然,字符串 "ABCDABD" 的 $Next$ 数组变成了 $left{-1, 0, 0, 0, -1, 0, 2 ight}$ (之前是 $left{-1, 0, 0, 0, 0, 1, 2 ight}$ )
KMP算法及其他
有了 $Next$ 数组,KMP算法就特别懒人化了。本身KMP也是非常板子化的算法。
#include <iostream> #include <string> using namespace std; const int maxn = 1e5+5; int Next[maxn]; void GetNext(const string &p){ int p_len = p.size(); int i = 0; int j = -1; Next[i] = -1; while(i < p_len){ if(j == -1 || p[i] == p[j]){ i++; j++; if(p[i] != p[j]) Next[i] = j; else Next[i] = Next[j]; } else j = Next[j]; } return; } int KMP(const string &s, const string &p){ GetNext(p); int i = 0; int j = 0; int s_len = s.size(); int p_len = p.size(); while(i < s_len && j < p_len){ if(j == -1 || s[i] == p[j]){ i++; j++; } else j = Next[j]; } if(j == p_len) return i - j; else return -1; }
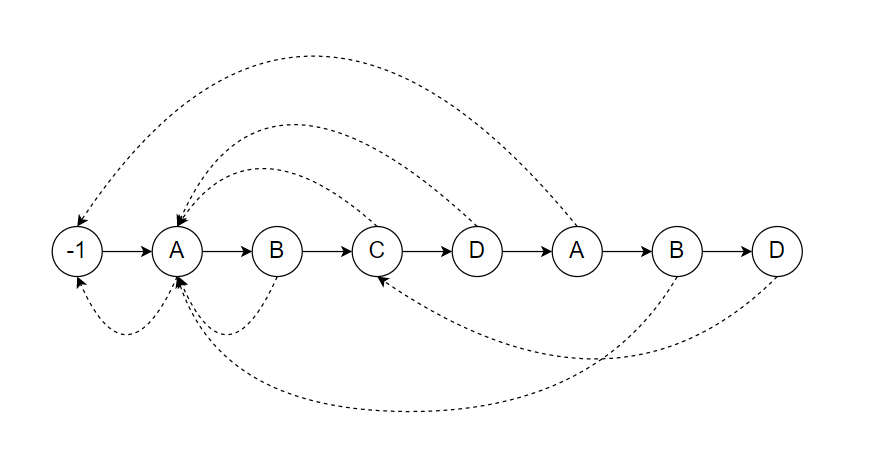
应该能发现我的这篇KMP博客不太像其他人的博客一样很多很长算法研究的段落语句,其实把KMP算法完全领悟之后,会越来越觉得KMP其实没有许多要说的东西,反而KMP算法教会了一个很关键的工具,即失配指针。
在KMP算法中,$Next$ 数组就是很多个失配指针,用来将失配状态转移到到其他可以继续匹配或者结束的状态,细心的人会发现,所有的状态转移也只不过是在一个范围内,很明显这是一个有限自动状态机,拿字符串 "ABCDABD" 来说,它的 $Next$ 数组为 $left{ -1, 0, 0, 0, -1, 0, 2 ight}$,对应的有限状态机为(虚线为失配状态转移,实线为匹配状态转移)