选择排序

前言

选择排序：每趟从待排序的记录中选出关键字最小的记录，顺序放在已排序的记录序列末尾，直到全部排序结束为止。

算法思想

简单选择排序很简单，它的大致处理流程为：

• 从待排序序列中，找到关键字最小的元素；
• 如果最小元素不是待排序序列的第一个元素，将其和第一个元素互换；
• 从余下的 N - 1 个元素中，找出关键字最小的元素，重复(1)、(2)步，直到排序结束。

动态效果示意图：

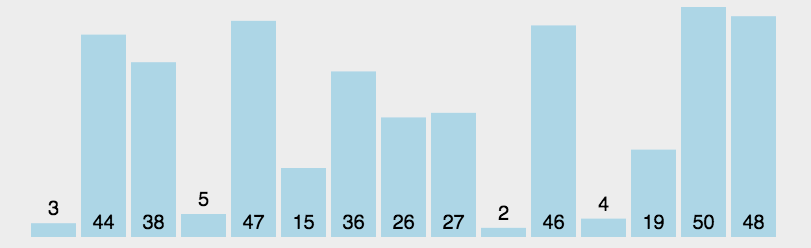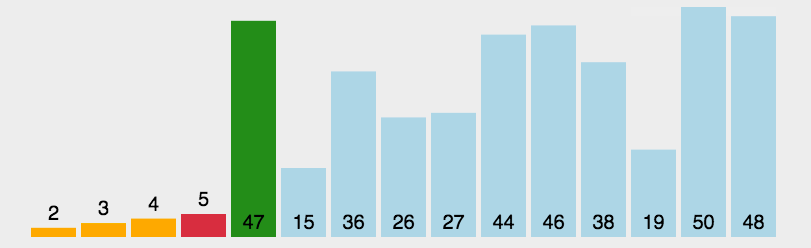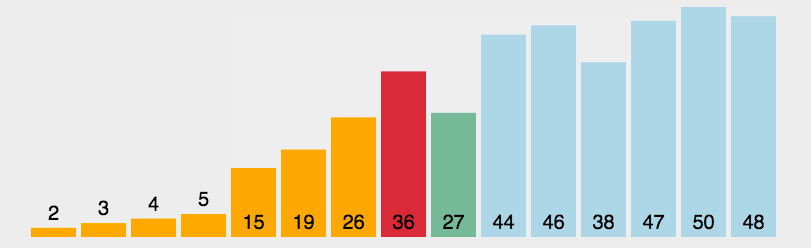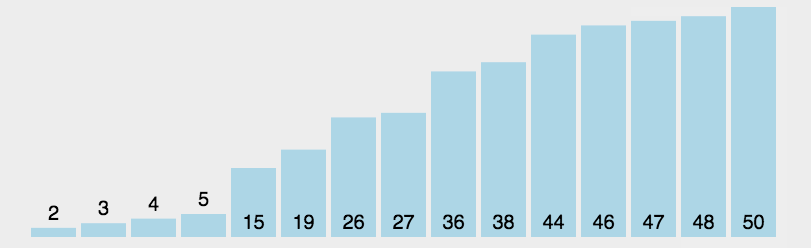
举例说明，处理过程示意图如下所示：

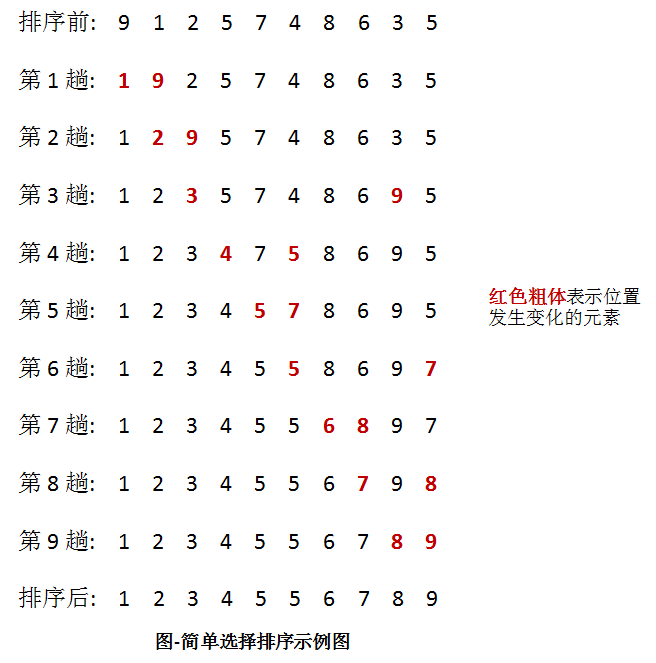
如图所示，每趟排序中，将当前第 i 小的元素放在位置 i 上。

代码

​ Python：列表排序

# -*- coding:utf-8 -*-
 
def SelectSort(input_list):
    '''
    函数说明:简单选择排序（升序）
    Parameters:
        input_list - 待排序列表
    Returns:
        sorted_list - 升序排序好的列表
    '''    
    if len(input_list) == 0:
        return []
    sorted_list = input_list
    length = len(sorted_list)
    for i in range(length):
        min_index = i
        for j in range(i + 1, length):
            if sorted_list[min_index] > sorted_list[j]:
                min_index = j
        if min_index == i:
            continue
        temp = sorted_list[i]
        sorted_list[i] = sorted_list[min_index]
        sorted_list[min_index] = temp
        # 上面三步交换也可以使用交叉赋值
    return sorted_list
 
if __name__ == '__main__':
    input_list = [6, 4, 8, 9, 2, 3, 1]
    print('排序前:', input_list)
    sorted_list = SelectSort(input_list)
    print('排序后:', sorted_list)

​ C：字符串排序

#include <stdio.h> 
#include <stdlib.h>
#include <string.h>
#define MAX 20				// 最大字符串长度

/* ---------------------------------------- */
/*  选择排序法                              */
/* ---------------------------------------- */
void select(char *string, int count)
{
   int pos;					// 目前最小的字符
   int i, j;
   char temp;

   for ( i = 0; i < count - 1; i++ )  	// 第一层循环
   {
      pos = i;
      temp = string[pos];
      /* 查找最小的字符 */
      for ( j = i + 1; j < count; j++ ) // 第二层循环
         if ( string[j] < temp )        // 是否更小
         {
            pos = j;              		// 新的最小字符
            temp = string[j];
         }
      string[pos] = string[i];    		// 交换两字符
      string[i] = temp;
      printf("输出结果: [%s]
", string); // 输出交换后字符串
   }
}

/* ---------------------------------------- */
/*  主程序: 输入字符串后将字符串排序           */
/* ---------------------------------------- */
int main(void)
{
   char string[MAX];              // 字符串数组
   int count;                     // 字符串长度

   printf("输入要排序的字符串 ==> ");
   gets(string);                  // 读取字符串
   count = strlen(string);        // 计算字符串长度
   select(string, count);         // 选择排序法
   printf("
输出排序结果: [%s]
",string);	// 输出排序后字符串
}

算法分析

简单算法排序性能

时间复杂度

简单选择排序的比较次数与序列的初始排序无关。假设待排序的序列有 N 个元素，则比较次数总是 N (N-1)/ 2。

而移动次数与序列的初始排序有关。当序列正序时，移动次数最少，为 0 。

当序列反序时，移动次数最多，为 3N (N - 1) / 2。

所以，综合以上，简单排序的时间复杂度为 O(N²)。

空间复杂度

简单选择排序需要占用 1 个临时空间，用于保存最小值得索引。

本站整理自：

http://www.cnblogs.com/jingmoxukong/p/4303289.html