定义
线段树(Segment Tree)是一种二叉搜索树,它将一个区间不断二分,分成两个区间,直到最后只剩一个单元区间即长度为 1 的区间。每个单元区间对应线段树中的一个叶子结点。
线段树进行更新(update)操作的时间复杂度为O(logn),进行区间查询(range query)操作的时间复杂度也为O(logn)。
实现原理
结构
- 线段树是平衡二叉树。(最大深度和最小深度之差不大于 1)
- 线段树不是完全二叉树,但可以把不存在结点看作 null,即看似是完全二叉树。
- 线段树是用一个数组保存的。
- 线段树中只有度为 2 或 0的结点,因为是区间不断二分生成的。
结构图:
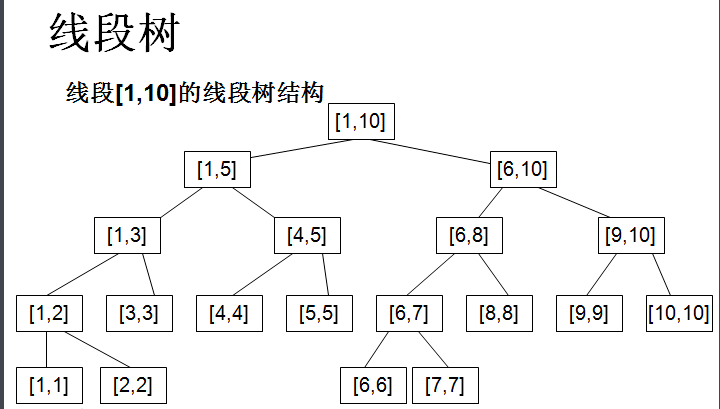
二叉树的特性
- 一颗二叉树中,若度为 2 的结点数为 n2,度为 0 的结点数(即叶子结点数)为 n0。则 n0 = n2 + 1。
- 对 k 层满二叉树:
- 一共有 2k - 1个结点。
- 不计最后一层,即前 k - 1 层结点数之和为 2k-1 - 1。
- 最后一层有 2k-1 个结点。
- 最后一层结点数比前 k - 1 层结点数还要多 1。
空间需求
-
理论空间需求:若叶子结点数为 n,则非叶子结点数为 n - 1,所需空间为 2n - 1。
如上图中,有 10 个单位区间,即 10 个叶子结点,所以非叶子结点有 9 个,一共需要 19 个空间。的确如此,但是我们发现最后一层中间是空的,我们要把它补上。这就导致实际空间需求并不止这么多。
-
实际空间需求:4n - 1
- 最完美的情况就是刚好是满二叉树,叶子结点都在最后一层,若叶子结点数为 n,这时只需 2n - 1 的空间。(通常我们直接开 2n 空间)
- 但若在此时增加一个叶子结点,将需要开一层的空间(开一整层的原因是,你并不知道这个新结点是在最后一层的哪个位置,如果在最右边的话,需要开一整层的空间),最后一层的空间大小是前面所有层结点数之和再加1。所以空间需求是 2n - 1 + 2n 即 4n - 1。(通常我们直接开 4n 空间)
这就是为什么需要四倍空间的原因了。
线段树的构建
- 线段树的构建是自底向上构建的,从每个叶子结点往上,除了叶子结点,其它结点的值都是根据左右孩子结点的值计算得出的。这个计算过程可能依所需要处理的问题不同而不同(例如对于保存区间最小值的线段树来说,merge的过程应为
min()函数,可以求最小值、最大值、总和、最大公约数、最小公倍数等)。 - 线段树下标从 0 开始,则左孩子结点下标为 2 * index + 1,右孩子结点下标为 2 * index + 2。
合成器代码:
package datastructure.tree;
/**
* 合成器,使线段树可以自定义生成方式
*
* @author holiday
* @version 1.0
* @date 2019-10-07 16:18
*/
public interface Merger<E> {
/**
* 合成方法,计算出的父结点对应的值
*
* @param a 父结点下的左结点
* @param b 父结点下的右结点
* @return 根据a和b,计算出的父结点对应的值
*/
E merge(E a, E b);
}
线段树代码:
package datastructure.tree;
/**
* 线段树
*
* @author holiday
* @version 1.0
* @date 2019-10-07 16:19
*/
public class SegmentTree<E> {
/**
* 线段树中的结点,其中父结点的值为它的两个子结点 merge 后的值
*/
private E[] tree;
/**
* 生成线段树所用的数组,即各叶子结点
*/
private E[] data;
/**
* 合成器,构造线段树时候同时传入合成器
*/
private Merger<E> merger;
public SegmentTree(E[] data, Merger<E> merger) {
this.merger = merger;
this.data = (E[]) new Object[data.length];
// 复制原始数据到 data 中
System.arraycopy(data, 0, this.data, 0, data.length);
// 开4倍空间
tree = (E[]) new Object[4 * data.length];
// 构造线段树
build(0, 0, data.length - 1);
}
/**
* 构建线段树
*
* @param treeIndex 当前结点的下标
* @param treeLeft 当前树的左边界
* @param treeRight 当前树的右边界
*/
private void build(int treeIndex, int treeLeft, int treeRight) {
// 已经到叶子结点
if (treeLeft == treeRight) {
tree[treeIndex] = data[treeLeft];
return;
}
// 获得左右孩子下标
int leftChildIndex = getLeftChildIndex(treeIndex);
int rightChildIndex = getRightChileIndex(treeIndex);
// 取中点
int mid = (treeLeft + treeRight) >>> 1;
// 先构造左右孩子结点
build(leftChildIndex, treeLeft, mid);
build(rightChildIndex, mid + 1, treeRight);
// 根据左右孩子结点的值,通过合成器决定父结点的值
tree[treeIndex] = merger.merge(tree[leftChildIndex], tree[rightChildIndex]);
}
/**
* 返回左孩子的下标
*
* @param index 当前结点的下标
* @return 左孩子的下标
*/
private int getLeftChildIndex(int index) {
return 2 * index + 1;
}
/**
* 返回右孩子的下标
*
* @param index 当前结点的下标
* @return 右孩子的下标
*/
private int getRightChileIndex(int index) {
return 2 * index + 2;
}
/**
* 获得线段树的大小
*
* @return size
*/
public int getSize() {
return data.length;
}
/**
* 获得 data 数组下标为 index 的值。
*
* @param index data 数组下标
* @return data[index]
*/
public E get(int index) {
if (index < 0 || index >= data.length) {
throw new IllegalArgumentException("Index is illegal.");
}
return data[index];
}
/**
* 打印结果测试
*
* @return
*/
@Override
public String toString() {
StringBuilder s = new StringBuilder();
s.append('[');
for (int i = 0; i < tree.length; i++) {
if (tree[i] != null) {
s.append(tree[i]);
} else {
s.append("null");
}
if (i != tree.length - 1) {
s.append(", ");
}
}
s.append(']');
return s.toString();
}
}
线段树的查询
/**
* 返回区间 [left,right] 的值
*
* @param left 查询的左边界
* @param right 查询的右边界
* @return result
*/
public E query(int left, int right) {
if (left < 0 || right >= data.length || left > right) {
throw new IllegalArgumentException("Index is illegal");
}
return queryRange(0, 0, data.length - 1, left, right);
}
/**
* 递归查询
*
* @param treeIndex 当前结点的下标
* @param treeLeft 当前树的左边界
* @param treeRight 当前树的右边界
* @param queryLeft 查询的左边界
* @param queryRight 查询的右边界
* @return result
*/
private E queryRange(int treeIndex, int treeLeft, int treeRight, int queryLeft, int queryRight) {
// 范围正好对应
if (queryLeft == treeLeft && queryRight == treeRight) {
return tree[treeIndex];
}
// 获得左右孩子下标
int leftChildIndex = getLeftChildIndex(treeIndex);
int rightChildIndex = getRightChileIndex(treeIndex);
// 取中点
int mid = (treeLeft + treeRight) >>> 1;
// 若查询的左边界都大于中点,说明区间完全在右子树;若查询的右边界都小于等于中点,说明区间完全在左子树。
if (queryLeft > mid) {
return queryRange(rightChildIndex, mid + 1, treeRight, queryLeft, queryRight);
} else if (queryRight <= mid) {
return queryRange(leftChildIndex, treeLeft, mid, queryLeft, queryRight);
}
// 否则,左右子树都有
E leftResult = queryRange(leftChildIndex, treeLeft, mid, queryLeft, mid);
E rightResult = queryRange(rightChildIndex, mid + 1, treeRight, mid + 1, queryRight);
// 左右区间结果合并
E result = merger.merge(leftResult, rightResult);
return result;
}
练习题目
传送门:[LeetCode] 303. 区域和检索 - 数组不可变
线段树的单点更新
/**
* 在线段树中修改 data 数组下标为 index 的值为 val
*
* @param index data 数组下标
* @param val 新值
*/
public void set(int index, E val) {
if (index < 0 || index >= data.length) {
throw new IllegalArgumentException("Index is illegal");
}
data[index] = val;
update(0, 0, data.length - 1, index, val);
}
/**
* 更新线段树
*
* @param treeIndex 当前结点的下标
* @param treeLeft 当前树的左边界
* @param treeRight 当前树的左边界
* @param index data 数组下标
* @param val 新值
*/
private void update(int treeIndex, int treeLeft, int treeRight, int index, E val) {
// 已经递归到 data 数组中对应的叶子结点值
if (treeLeft == treeRight) {
tree[treeIndex] = val;
return;
}
// 获得左右孩子下标
int leftChildIndex = getLeftChildIndex(treeIndex);
int rightChildIndex = getRightChileIndex(treeIndex);
// 取中点
int mid = (treeLeft + treeRight) >>> 1;
// 若修改的下标大于中点,说明在右子树,否则在左子树
if (index > mid) {
update(rightChildIndex, mid + 1, treeRight, index, val);
} else {
update(leftChildIndex, treeLeft, mid, index, val);
}
// 根据修改完的左右孩子节点来重新用合成器生成父结点值
tree[treeIndex] = merger.merge(tree[leftChildIndex], tree[rightChildIndex]);
}
练习题目
传送门:[LeetCode] 307. 区域和检索 - 数组可修改
线段树代码
package datastructure.tree;
/**
* 线段树
*
* @author holiday
* @version 1.0
* @date 2019-10-07 16:19
*/
public class SegmentTree<E> {
/**
* 线段树中的结点,其中父结点的值为它的两个子结点 merge 后的值
*/
private E[] tree;
/**
* 生成线段树所用的数组,即各叶子结点
*/
private E[] data;
/**
* 合成器,构造线段树时候同时传入合成器
*/
private Merger<E> merger;
public SegmentTree(E[] data, Merger<E> merger) {
this.merger = merger;
this.data = (E[]) new Object[data.length];
// 复制原始数据到 data 中
System.arraycopy(data, 0, this.data, 0, data.length);
// 开4倍空间
tree = (E[]) new Object[4 * data.length];
// 构造线段树
build(0, 0, data.length - 1);
}
/**
* 构建线段树
*
* @param treeIndex 当前结点的下标
* @param treeLeft 当前树的左边界
* @param treeRight 当前树的右边界
*/
private void build(int treeIndex, int treeLeft, int treeRight) {
// 已经到叶子结点
if (treeLeft == treeRight) {
tree[treeIndex] = data[treeLeft];
return;
}
// 获得左右孩子下标
int leftChildIndex = getLeftChildIndex(treeIndex);
int rightChildIndex = getRightChileIndex(treeIndex);
// 取中点
int mid = (treeLeft + treeRight) >>> 1;
// 先构造左右孩子结点
build(leftChildIndex, treeLeft, mid);
build(rightChildIndex, mid + 1, treeRight);
// 根据左右孩子结点的值,通过合成器决定父结点的值
tree[treeIndex] = merger.merge(tree[leftChildIndex], tree[rightChildIndex]);
}
/**
* 返回区间 [left,right] 的值
*
* @param left 查询的左边界
* @param right 查询的右边界
* @return result
*/
public E query(int left, int right) {
if (left < 0 || right >= data.length || left > right) {
throw new IllegalArgumentException("Index is illegal");
}
return queryRange(0, 0, data.length - 1, left, right);
}
/**
* 递归查询
*
* @param treeIndex 当前结点的下标
* @param treeLeft 当前树的左边界
* @param treeRight 当前树的右边界
* @param queryLeft 查询的左边界
* @param queryRight 查询的右边界
* @return result
*/
private E queryRange(int treeIndex, int treeLeft, int treeRight, int queryLeft, int queryRight) {
// 范围正好对应
if (queryLeft == treeLeft && queryRight == treeRight) {
return tree[treeIndex];
}
// 获得左右孩子下标
int leftChildIndex = getLeftChildIndex(treeIndex);
int rightChildIndex = getRightChileIndex(treeIndex);
// 取中点
int mid = (treeLeft + treeRight) >>> 1;
// 若查询的左边界都大于中点,说明区间完全在右子树;若查询的右边界都小于等于中点,说明区间完全在左子树。
if (queryLeft > mid) {
return queryRange(rightChildIndex, mid + 1, treeRight, queryLeft, queryRight);
} else if (queryRight <= mid) {
return queryRange(leftChildIndex, treeLeft, mid, queryLeft, queryRight);
}
// 否则,左右子树都有
E leftResult = queryRange(leftChildIndex, treeLeft, mid, queryLeft, mid);
E rightResult = queryRange(rightChildIndex, mid + 1, treeRight, mid + 1, queryRight);
// 左右区间结果合并
E result = merger.merge(leftResult, rightResult);
return result;
}
/**
* 在线段树中修改 data 数组下标为 index 的值为 val
*
* @param index data 数组下标
* @param val 新值
*/
public void set(int index, E val) {
if (index < 0 || index >= data.length) {
throw new IllegalArgumentException("Index is illegal");
}
data[index] = val;
update(0, 0, data.length - 1, index, val);
}
/**
* 更新线段树
*
* @param treeIndex 当前结点的下标
* @param treeLeft 当前树的左边界
* @param treeRight 当前树的左边界
* @param index data 数组下标
* @param val 新值
*/
private void update(int treeIndex, int treeLeft, int treeRight, int index, E val) {
// 已经递归到 data 数组中对应的叶子结点值
if (treeLeft == treeRight) {
tree[treeIndex] = val;
return;
}
// 获得左右孩子下标
int leftChildIndex = getLeftChildIndex(treeIndex);
int rightChildIndex = getRightChileIndex(treeIndex);
// 取中点
int mid = (treeLeft + treeRight) >>> 1;
// 若修改的下标大于中点,说明在右子树,否则在左子树
if (index > mid) {
update(rightChildIndex, mid + 1, treeRight, index, val);
} else {
update(leftChildIndex, treeLeft, mid, index, val);
}
// 根据修改完的左右孩子节点来重新用合成器生成父结点值
tree[treeIndex] = merger.merge(tree[leftChildIndex], tree[rightChildIndex]);
}
/**
* 返回左孩子的下标
*
* @param index 当前结点的下标
* @return 左孩子的下标
*/
private int getLeftChildIndex(int index) {
return 2 * index + 1;
}
/**
* 返回右孩子的下标
*
* @param index 当前结点的下标
* @return 右孩子的下标
*/
private int getRightChileIndex(int index) {
return 2 * index + 2;
}
/**
* 获得线段树的大小
*
* @return size
*/
public int getSize() {
return data.length;
}
/**
* 获得 data 数组下标为 index 的值。
*
* @param index data 数组下标
* @return data[index]
*/
public E get(int index) {
if (index < 0 || index >= data.length) {
throw new IllegalArgumentException("Index is illegal.");
}
return data[index];
}
/**
* 打印结果测试
*
* @return
*/
@Override
public String toString() {
StringBuilder s = new StringBuilder();
s.append('[');
for (int i = 0; i < tree.length; i++) {
if (tree[i] != null) {
s.append(tree[i]);
} else {
s.append("null");
}
if (i != tree.length - 1) {
s.append(", ");
}
}
s.append(']');
return s.toString();
}
}
小结
区间更新还没有看,等以后做到这类题再看了。