机器学习sklearn（50）： 特征工程（十七） 特征降维（八）降维算法PCA和SVD（三）PCA与SVD

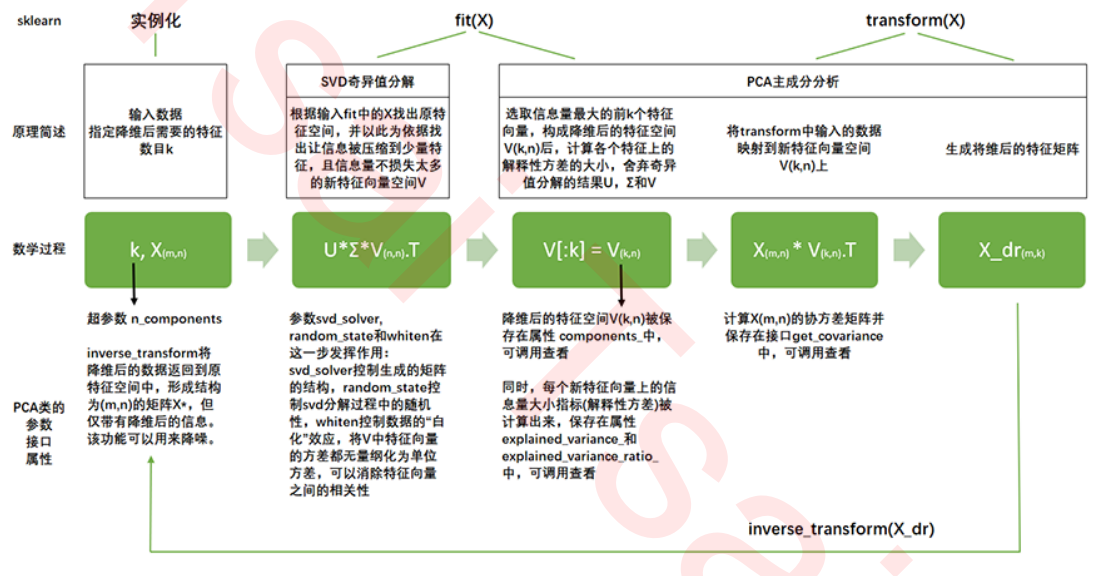
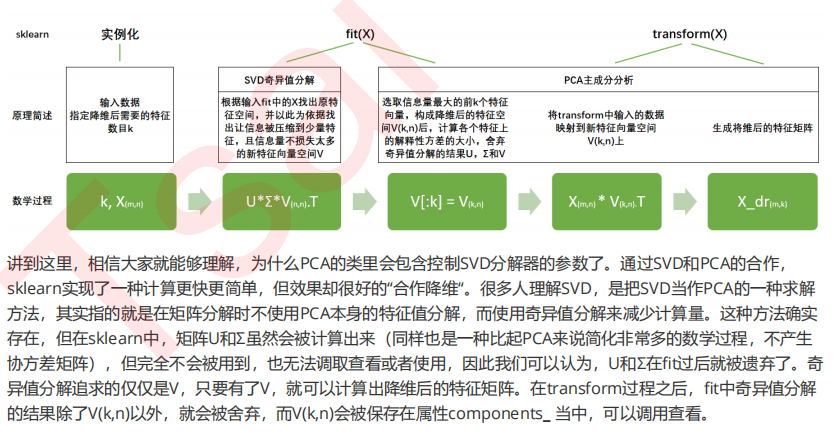
3 PCA中的SVD

3.1 PCA中的SVD哪里来？

 

PCA(2).fit(X).components_
PCA(2).fit(X).components_.shape

3.2 重要参数svd_solver 与 random_state 

3.3 重要属性components_

1. 导入需要的库和模块

from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

2. 实例化数据集，探索数据

faces = fetch_lfw_people(min_faces_per_person=60)
faces.images.shape
#怎样理解这个数据的维度？
faces.data.shape
#换成特征矩阵之后，这个矩阵是什么样？
X = faces.data

3. 看看图像什么样？将原特征矩阵进行可视化

#数据本身是图像，和数据本身只是数字，使用的可视化方法不同
#创建画布和子图对象
fig, axes = plt.subplots(4,5
                       ,figsize=(8,4)
                       ,subplot_kw = {"xticks":[],"yticks":[]} #不要显示坐标轴
                       )
fig
axes
#不难发现，axes中的一个对象对应fig中的一个空格
#我们希望，在每一个子图对象中填充图像（共24张图），因此我们需要写一个在子图对象中遍历的循环
axes.shape
#二维结构，可以有两种循环方式，一种是使用索引，循环一次同时生成一列上的三个图
#另一种是把数据拉成一维，循环一次只生成一个图
#在这里，究竟使用哪一种循环方式，是要看我们要画的图的信息，储存在一个怎样的结构里
#我们使用 子图对象.imshow 来将图像填充到空白画布上
#而imshow要求的数据格式必须是一个(m,n)格式的矩阵，即每个数据都是一张单独的图
#因此我们需要遍历的是faces.images，其结构是(1277, 62, 47)
#要从一个数据集中取出24个图，明显是一次性的循环切片[i,:,:]来得便利
#因此我们要把axes的结构拉成一维来循环
axes.flat
enumerate(axes.flat) #填充图像
for i, ax in enumerate(axes.flat):
    ax.imshow(faces.images[i,:,:] 
             ,cmap="gray" #选择色彩的模式
             )
#https://matplotlib.org/tutorials/colors/colormaps.html

4. 建模降维，提取新特征空间矩阵 

#原本有2900维，我们现在来降到150维
pca = PCA(150).fit(X) 
V = pca.components_
V.shape

5. 将新特征空间矩阵可视化

fig, axes = plt.subplots(3,8,figsize=(8,4),subplot_kw = {"xticks":[],"yticks":[]})
for i, ax in enumerate(axes.flat):
    ax.imshow(V[i,:].reshape(62,47),cmap="gray")

4 重要接口inverse_transform

4.1 迷你案例：用人脸识别看PCA降维后的信息保存量

1. 导入需要的库和模块(与3.3节中步骤一致) 

from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

2. 导入数据，探索数据(与2.3.3节中步骤一致)

faces = fetch_lfw_people(min_faces_per_person=60)
faces.images.shape
#怎样理解这个数据的维度？
faces.data.shape
#换成特征矩阵之后，这个矩阵是什么样？
X = faces.data

3. 建模降维，获取降维后的特征矩阵X_dr

pca = PCA(150)
X_dr = pca.fit_transform(X)
X_dr.shape

4. 将降维后矩阵用inverse_transform返回原空间

X_inverse = pca.inverse_transform(X_dr)
X_inverse.shape

5. 将特征矩阵X和X_inverse可视化

fig, ax = plt.subplots(2,10,figsize=(10,2.5)
                     ,subplot_kw={"xticks":[],"yticks":[]}
                     )
#和2.3.3节中的案例一样，我们需要对子图对象进行遍历的循环，来将图像填入子图中
#那在这里，我们使用怎样的循环？
#现在我们的ax中是2行10列，第一行是原数据，第二行是inverse_transform后返回的数据
#所以我们需要同时循环两份数据，即一次循环画一列上的两张图，而不是把ax拉平
for i in range(10):
    ax[0,i].imshow(faces.images[i,:,:],cmap="binary_r")
    ax[1,i].imshow(X_inverse[i].reshape(62,47),cmap="binary_r")

4.2 迷你案例：用PCA做噪音过滤

 

1. 导入所需要的库和模块

from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

2. 导入数据，探索数据

digits = load_digits()
digits.data.shape

3. 定义画图函数 

def plot_digits(data):
    fig, axes = plt.subplots(4,10,figsize=(10,4)
                           ,subplot_kw = {"xticks":[],"yticks":[]}
                           )
    for i, ax in enumerate(axes.flat):
        ax.imshow(data[i].reshape(8,8),cmap="binary")
        
plot_digits(digits.data)

4. 为数据加上噪音

np.random.RandomState(42) #在指定的数据集中，随机抽取服从正态分布的数据
#两个参数，分别是指定的数据集，和抽取出来的正太分布的方差
noisy = np.random.normal(digits.data,2)
plot_digits(noisy)

5. 降维 

pca = PCA(0.5).fit(noisy)
X_dr = pca.transform(noisy)
X_dr.shape

6. 逆转降维结果，实现降噪

without_noise = pca.inverse_transform(X_dr)
plot_digits(without_noise)

 

5 重要接口，参数和属性总结