在机器学习中,通过增加一些输入数据的非线性特征来增加模型的复杂度通常是有效的。一个简单通用的办法是使用多项式特征,这可以获得特征的更高维度和互相间关系的项。这在 PolynomialFeatures 中实现:
>>> import numpy as np >>> from sklearn.preprocessing import PolynomialFeatures >>> X = np.arange(6).reshape(3, 2) >>> X array([[0, 1], [2, 3], [4, 5]]) >>> poly = PolynomialFeatures(2) >>> poly.fit_transform(X) array([[ 1., 0., 1., 0., 0., 1.], [ 1., 2., 3., 4., 6., 9.], [ 1., 4., 5., 16., 20., 25.]])
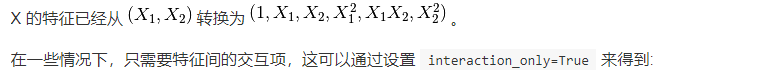
>>> X = np.arange(9).reshape(3, 3) >>> X array([[0, 1, 2], [3, 4, 5], [6, 7, 8]]) >>> poly = PolynomialFeatures(degree=3, interaction_only=True) >>> poly.fit_transform(X) array([[ 1., 0., 1., 2., 0., 0., 2., 0.], [ 1., 3., 4., 5., 12., 15., 20., 60.], [ 1., 6., 7., 8., 42., 48., 56., 336.]])
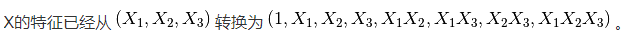
注意,当使用多项的 Kernel functions 时 ,多项式特征被隐式地在核函数中被调用(比如, sklearn.svm.SVC , sklearn.decomposition.KernelPCA )。
创建并使用多项式特征的岭回归实例请见 Polynomial interpolation 。
class sklearn.preprocessing.PolynomialFeatures(degree=2, *, interaction_only=False, include_bias=True, order='C')
Generate polynomial and interaction features.
Generate a new feature matrix consisting of all polynomial combinations of the features with degree less than or equal to the specified degree. For example, if an input sample is two dimensional and of the form [a, b], the degree-2 polynomial features are [1, a, b, a^2, ab, b^2].
- Parameters
- degreeint, default=2
-
The degree of the polynomial features.
- interaction_onlybool, default=False
-
If true, only interaction features are produced: features that are products of at most
degreedistinct input features (so notx[1] ** 2,x[0] * x[2] ** 3, etc.). - include_biasbool, default=True
-
If True (default), then include a bias column, the feature in which all polynomial powers are zero (i.e. a column of ones - acts as an intercept term in a linear model).
- order{‘C’, ‘F’}, default=’C’
-
Order of output array in the dense case. ‘F’ order is faster to compute, but may slow down subsequent estimators.
New in version 0.21.
- Attributes
- powers_ndarray of shape (n_output_features, n_input_features)
-
powers_[i, j] is the exponent of the jth input in the ith output.
- n_input_features_int
-
The total number of input features.
- n_output_features_int
-
The total number of polynomial output features. The number of output features is computed by iterating over all suitably sized combinations of input features.
Methods
|
|
Compute number of output features. |
|
|
Fit to data, then transform it. |
|
|
Return feature names for output features |
|
|
Get parameters for this estimator. |
|
|
Set the parameters of this estimator. |
|
|
Transform data to polynomial features |
Examples
>>> import numpy as np >>> from sklearn.preprocessing import PolynomialFeatures >>> X = np.arange(6).reshape(3, 2) >>> X array([[0, 1], [2, 3], [4, 5]]) >>> poly = PolynomialFeatures(2) >>> poly.fit_transform(X) array([[ 1., 0., 1., 0., 0., 1.], [ 1., 2., 3., 4., 6., 9.], [ 1., 4., 5., 16., 20., 25.]]) >>> poly = PolynomialFeatures(interaction_only=True) >>> poly.fit_transform(X) array([[ 1., 0., 1., 0.], [ 1., 2., 3., 6.], [ 1., 4., 5., 20.]])