1 数据流编程简介
在我们深入研究流处理的基础知识之前,让我们来看看在数据流程编程的背景和使用的术语。
1.1 数据流图
顾名思义,数据流程序描述了数据如何在算子之间流动。数据流程序通常表示为有向图,其中节点称为算子,用来表示计算,边表示数据之间的依赖性。算子是数据流程序的基本功能单元。他们从输入消耗数据,对它们执行计算,并生成数据输出用于进一步处理。一个数据流图必须至少有一个数据源和一个数据接收器。
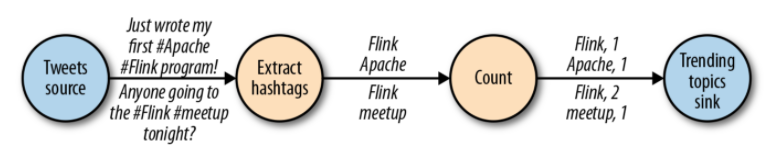
像图2-1中的数据流图被称为逻辑流图,因为它们表示了计算逻辑的高级视图。为了执行一个数据流程序,Flink会将逻辑流图转换为物理数据流图,详细说明程序的执行方式。例如,如果我们使用分布式处理引擎,每个算子在不同的物理机器可能有几个并行的任务运行。图2-2显示了图2-1逻辑图的物理数据流图。而在逻辑数据流图中节点表示算子,在物理数据流图中,节点是任务。“Extract hashtags”和“Count”算子有两个并行算子任务,每个算子任务对输入数据的子集执行计算

1.2 数据并行和任务并行
我们可以以不同方式利用数据流图中的并行性。第一,我们可以对输入数据进行分区,并在数据的子集上并行执行具有相同算子的任务并行。这种类型的并行性被称为数据并行性。数据并行是有用的,因为它允许处理大量数据,并将计算分散到不同的计算节点上。第二,我们可以将不同的算子在相同或不同的数据上并行执行。这种并行性称为任务并行性。使用任务并行性,我们可以更好地利用计算资源。
1.3 数据交换策略
数据交换策略定义了在物理执行流图中如何将数据分配给任务。数据交换策略可以由执行引擎自动选择,具体取决于算子的语义或我们明确指定的语义。在这里,我们简要回顾一些常见的数据交换策略,如图2-3所示。

- 前向策略将数据从一个任务发送到接收任务。如果两个任务都位于同一台物理计算机上(这通常由任务调度器确保),这种交换策略可以避免网络通信。
- 广播策略将所有数据发送到算子的所有的并行任务上面去。因为这种策略会复制数据和涉及网络通信,所以代价相当昂贵。
- 基于键控的策略通过Key值(键)对数据进行分区保证具有相同Key的数据将由同一任务处理。在图2-2中,输出“Extract hashtags”算子使用键来分区(hashtag),以便count算子的任务可以正确计算每个#标签的出现次数。
- 随机策略统一将数据分配到算子的任务中去,以便均匀地将负载分配到不同的计算任务。
2 并行处理流数据
既然我们熟悉了数据流编程的基础知识,现在是时候看看这些概念如何应用于并行的处理数据流了。但首先,让我们定义术语数据流:数据流是一个可能无限的事件序列。
数据流中的事件可以表示监控数据,传感器测量数据,信用卡交易数据,气象站观测数据,在线用户交互数据,网络搜索数据等。在本节中,我们将学习如何并行处理无限流,使用数据流编程范式。
2.1 延迟和吞吐量
流处理程序不同与批处理程序。在评估性能时,要求也有所不同。对于批处理程序,我们通常关心一个作业的总的执行时间,或我们的处理引擎读取输入所需的时间,执行计算,并回写结果。由于流处理程序是连续运行的,输入可能是无界的,所以数据流处理中没有总执行时间的概念。 相反,流处理程序必须尽可能快的提供输入数据的计算结果。我们使用延迟和吞吐量来表征流处理的性能要求。
2.2 延迟
延迟表示处理事件所需的时间。它是接收事件和看到在输出中处理此事件的效果之间的时间间隔。要直观的理解延迟,考虑去咖啡店买咖啡。当你进入咖啡店时,可能还有其他顾客在里面。因此,你排队等候直到轮到你下订单。收银员收到你的付款并通知准备饮料的咖啡师。一旦你的咖啡准备好了,咖啡师会叫你的名字,你可以到柜台拿你的咖啡。服务延迟是从你进入咖啡店的那一刻起,直到你喝上第一口咖啡之间的时间间隔。
在数据流中,延迟是以时间为单位测量的,例如毫秒。根据应用程序,我们可能会关心平均延迟,最大延迟或百分位延迟。例如,平均延迟值为10ms意味着处理事件的平均时间在10毫秒内。或者,延迟值为95%,10ms表示95%的事件在10ms内处理完毕。平均值隐藏了处理延迟的真实分布,可能会让人难以发现问题。如果咖啡师在准备卡布奇诺之前用完了牛奶,你必须等到他们从供应室带来一些。虽然你可能会因为这么长时间的延迟而生气,但大多数其他客户仍然会感到高兴。
确保低延迟对于许多流应用程序来说至关重要,例如欺诈检测,系统警报,网络监控和提供具有严格服务水平协议的服务。低延迟是流处理的关键特性,它实现了我们所谓的实时应用程序。像Apache Flink这样的现代流处理器可以提供低至几毫秒的延迟。相比之下,传统批处理程序延迟通常从几分钟到几个小时不等。在批处理中,首先需要收集事件批次,然后才能处理它们。因此,延迟是受每个批次中最后一个事件的到达时间的限制。所以自然而然取决于批的大小。真正的流处理不会引入这样的人为延迟,因此可以实现真正的低延迟。真的流模型,事件一进入系统就可以得到处理。延迟更密切地反映了在每个事件上必须进行的实际工作。
2.3 吞吐量
吞吐量是衡量系统处理能力的指标,也就是处理速率。也就是说,吞吐量告诉我们每个时间单位系统可以处理多少事件。重温咖啡店的例子,如果商店营业时间为早上7点至晚上7点。当天为600个客户提供了服务,它的平均吞吐量将是每小时50个客户。虽然我们希望延迟尽可能低,但我们通常也需要吞吐量尽可能高。
吞吐量以每个时间单位系统所能处理的事件数量或操作数量来衡量。值得注意的是,事件处理速率取决于事件到达的速率,低吞吐量并不一定表示性能不佳。 在流式系统中,我们通常希望确保我们的系统可以处理最大的预期事件到达的速率。也就是说,我们主要的关注点在于确定的峰值吞吐量是多少,当系统处于最大负载时性能怎么样。为了更好地理解峰值吞吐量的概念,让我们考虑一个流处理 程序没有收到任何输入的数据,因此没有消耗任何系统资源。当第一个事件进来时,它会尽可能以最小延迟立即处理。例如,如果你是第一个出现在咖啡店的顾客,在早上开门后,你将立即获得服务。理想情况下,您希望此延迟保持不变 ,并且独立于传入事件的速率。但是,一旦我们达到使系统资源被完全使用的事件传入速率,我们将不得不开始缓冲事件。在咖啡店里 ,午餐后会看到这种情况发生。许多人出现在同一时间,必须排队等候。在此刻,咖啡店系统已达到其峰值吞吐量,进一步增加 事件传入的速率只会导致更糟糕的延迟。如果系统继续以可以处理的速率接收数据,缓冲区可能变为不可用,数据可能会丢失。这种情况是众所周知的 作为背压,有不同的策略来处理它。
2.4 延迟与吞吐量的对比
此时,应该清楚延迟和吞吐量不是独立指标。如果事件需要在处理流水线中待上很长时间,我们不能轻易确保高吞吐量。同样,如果系统容量很小,事件将被缓冲,而且必须等待才能得到处理。
让我们重温一下咖啡店的例子来阐明一下延迟和吞吐量如何相互影响。首先,应该清楚存在没有负载时的最佳延迟。也就是说,如果你是咖啡店的唯一客户,会很快得到咖啡。然而,在繁忙时期,客户将不得不排队等待,并且会有延迟增加。另一个影响延迟和吞吐量的因素是处理事件所花费的时间或为每个客户提供服务所花费的时间。想象一下,期间圣诞节假期,咖啡师不得不为每杯咖啡画圣诞老人。这意味着准备一杯咖啡需要的时间会增加,导致每个人花费 更多的时间在等待咖啡师画圣诞老人,从而降低整体吞吐量。
那么,你可以同时获得低延迟和高吞吐量吗?或者这是一个无望的努力?我们可以降低得到咖啡的延迟 ,方法是:聘请一位更熟练的咖啡师来准备咖啡。在高负载时,这种变化也会增加吞吐量,因为会在相同的时间内为更多的客户提供服务。 实现相同结果的另一种方法是雇用第二个咖啡师来利用并行性。这里的主要想法是降低延迟来增加吞吐量。当然,如果系统可以更快的执行操作,它可以在相同的时间内执行更多操作。 事实上,在流中利用并行性时也会发生这种情况。通过并行处理多个流,在同时处理更多事件的同时降低延迟。
3 数据流上的操作
流处理引擎通常提供一组内置操作:摄取(ingest),转换(transform)和输出流(output)。这些操作可以 结合到数据流图中来实现逻辑流处理程序。在本节中,我们描述最常见的流处理操作。
操作可以是无状态的或有状态的。无状态操作不保持任何内部状态。也就是说,事件的处理不依赖于过去看到的任何事件,也没有保留历史。 无状态操作很容易并行化,因为事件可以彼此独立地处理,也独立于事件到达的顺序(和事件到达顺序没有关系)。 而且,在失败的情况下,无状态操作可以是简单的重新启动并从中断处继续处理。相反, 有状态操作可能会维护之前收到的事件的信息。此状态可以通过传入事件更新,也可以用于未来事件的处理逻辑。有状态的流 处理应用程序更难以并行化和以容错的方式来运行,因为状态需要有效的进行分区和在发生故障的情况下可靠地恢复。
3.1 数据摄入和数据吞吐量
数据摄取和数据出口操作允许流处理程序与外部系统通信。数据摄取是操作从外部源获取原始数据并将其转换为其他格式(ETL)。实现数据提取逻辑的运算符被称为数据源。数据源可以从TCP Socket,文件,Kafka Topic或传感器数据接口中提取数据。数据出口是以适合消费的形式产出到外部系统。执行数据出口的运算符称为数据接收器,包括文件,数据库,消息队列和监控接口。
3.2 转换算子

转换算子是单遍处理算子,碰到一个事件处理一个事件。这些操作在使用后会消费一个事件,然后对事件数据做一些转换,产生一个新的输出流。转换逻辑可以集成在 操作符中或由UDF函数提供,如图所示图2-4。程序员编写实现自定义计算逻辑。
操作符可以接受多个输入流并产生多个输出流。他们还可以通过修改数据流图的结构要么将流分成多个流,要么将流合并为一条流。
3.3 滚动聚合
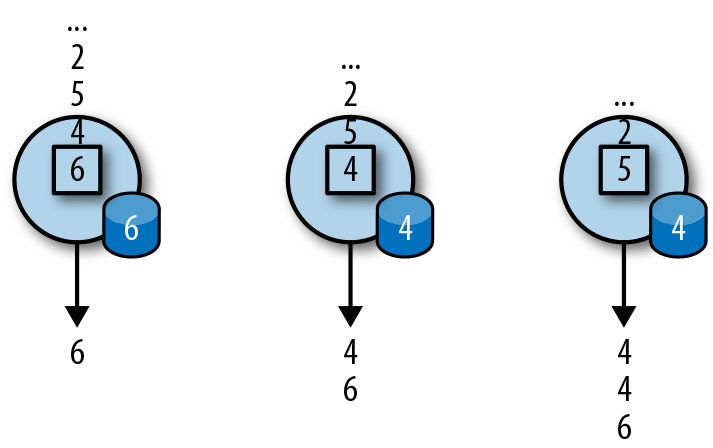
滚动聚合是一种聚合,例如sum,minimum和maximum,为每个输入事件不断更新。 聚合操作是有状态的,并将当前状态与传入事件一起计算以产生更新的聚合值。请注意能够有效地将当前状态与事件相结合 产生单个值,聚合函数必须是关联的和可交换的。否则,操作符必须存储完整的流数据历史。图2-5显示了最小滚动 聚合。操作符保持当前的最小值和相应地为每个传入的事件来更新最小值。
3.4 窗口操作符
转换和滚动聚合一次处理一个事件产生输出事件并可能更新状态。但是,有些操作必须收集并缓冲数据以计算其结果。 例如,考虑不同流之间的连接或整体聚合这样的操作,例如中值函数。为了在无界流上高效运行这些操作符,我们需要限制 这些操作维护的数据量。在本节中,我们将讨论窗口操作,提供此服务。
窗口还可以在语义上实现关于流的比较复杂的查询。我们已经看到了滚动聚合的方式,以聚合值编码整个流的历史数据来为每个事件提供低延迟的结果。 但如果我们只对最近的数据感兴趣的话会怎样?考虑给司机提供实时交通信息的应用程序。这个程序可以使他们避免拥挤的路线。在这种场景下,你想知道某个位置在最近几分钟内是否有事故发生。 另一方面,了解所有发生过的事故在这个应用场景下并没有什么卵用。更重要的是,通过将流历史缩减为单一聚合值,我们将丢失这段时间内数据的变化。例如,我们可能想知道每5分钟有多少车辆穿过 某个路口。
窗口操作不断从无限事件流中创建有限的事件集,好让我们执行有限集的计算。通常会基于数据属性或基于时间的窗口来分配事件。 要正确定义窗口运算符语义,我们需要确定如何给窗口分配事件以及对窗口中的元素进行求值的频率是什么样的。 窗口的行为由一组策略定义。窗口策略决定何时创建新的窗口以及要分配的事件属于哪个窗口,以及何时对窗口中的元素进行求值。 而窗口的求值基于触发条件。一旦触发条件得到满足,窗口的内容将会被发送到求值函数,求值函数会将计算逻辑应用于窗口中的元素。 求值函数可以是sum或minimal或自定义的聚合函数。 求值策略可以根据时间或者数据属性计算(例如,在过去五秒内收到的事件或者最近的一百个事件等等)。 接下来,我们描述常见窗口类型的语义。
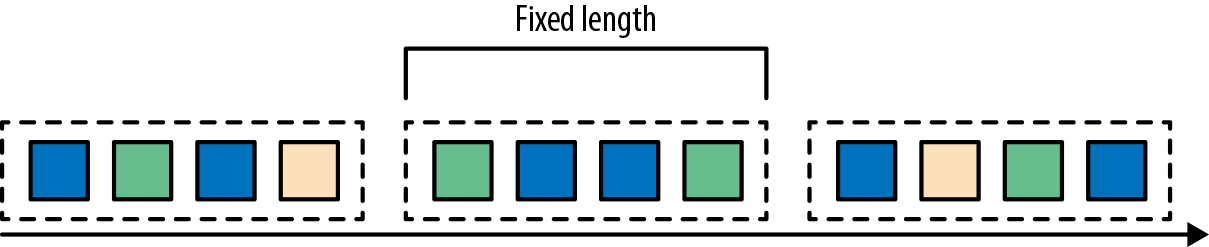
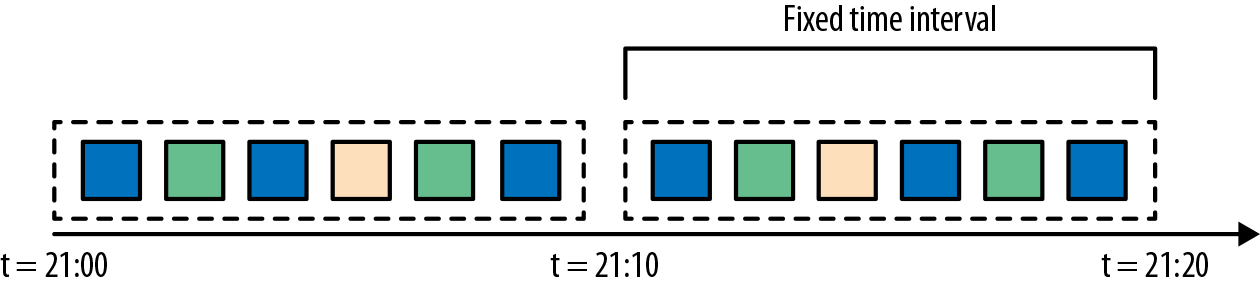
- 滚动窗口是将事件分配到固定大小的不重叠的窗口中。当通过窗口的结尾时,全部事件被发送到求值函数进行处理。基于计数的滚动窗口定义了在触发求值之前需要收集多少事件。图2-6显示了一个基于计数的翻滚窗口,每四个元素一个窗口。基于时间的滚动窗口定义一个时间间隔,包含在此时间间隔内的事件。图2-7显示了基于时间的滚动窗口,将事件收集到窗口中每10分钟触发一次计算。
- 滑动窗口将事件分配到固定大小的重叠的窗口中去。因此,事件可能属于多个桶。我们通过提供窗口的长度和滑动距离来定义滑动窗口。滑动距离定义了创建新窗口的间隔。基于滑动计数的窗口,图2-8的长度为四个事件,三个为滑动距离。
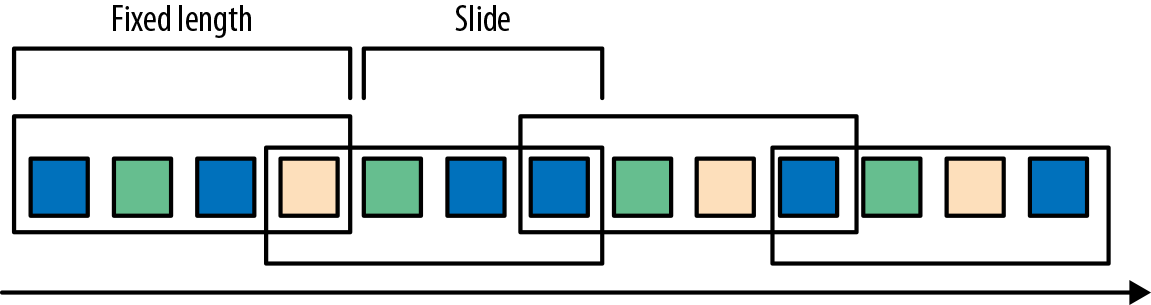
- 会话窗口在常见的真实场景中很有用,一些场景既不能使用滚动窗口也不能使用滑动窗口。考虑一个分析在线用户行为的应用程序。在应用程序里,我们想把源自同一时期的用户活动或会话事件分组在一起。会话由一系列相邻时间发生的事件组成,接下来有一段时间没有活动。例如,用户在App上浏览一系列的新闻,然后关掉App,那么浏览新闻这段时间的浏览事件就是一个会话。会话窗口事先没有定义窗口的长度,而是取决于数据的实际情况,滚动窗口和滑动窗口无法应用于这个场景。相反,我们需要将同一会话中的事件分配到同一个窗口中去,而不同的会话可能窗口长度不一样。会话窗口会定义一个间隙值来区分不同的会话。间隙值的意思是:用户一段时间内不活动,就认为用户的会话结束了。图2-9显示了一个会话窗口。

到目前为止,所有窗口类型都是在整条流上去做窗口操作。但实际上你可能想要将一条流分流成多个逻辑流并定义并行窗口。 例如,如果我们正在接收来自不同传感器的测量结果,那么可能想要在做窗口计算之前按传感器ID对流进行分流操作。 在并行窗口中,每条流都独立于其他流,然后应用了窗口逻辑。图2-10显示了一个基于计数的长度为2的并行滚动窗口,根据事件颜色分流。
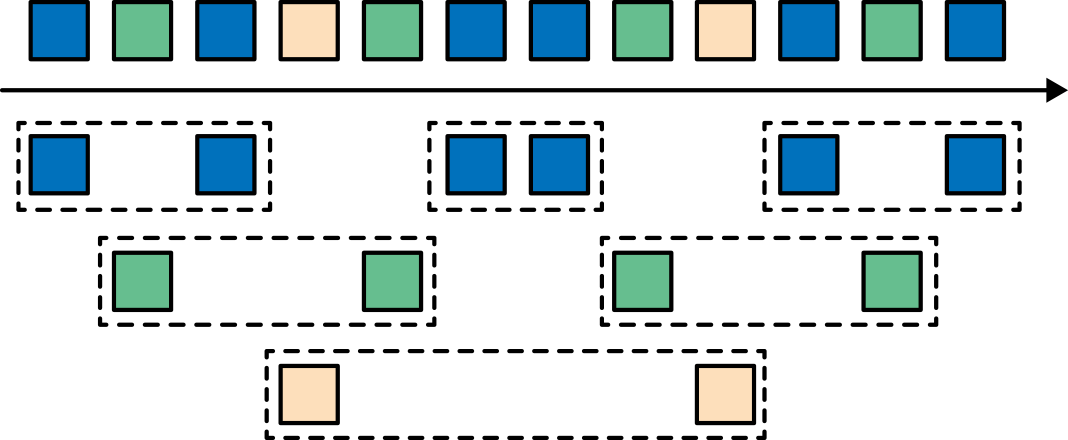
在流处理中,窗口操作与两个主要概念密切相关:时间语义和状态管理。时间也许是流处理最重要的方面。即使低延迟是流处理的一个有吸引力的特性,它的真正价值不仅仅是快速分析。真实世界的系统,网络和通信渠道远非完美,流数据经常被推迟或无序(乱序)到达。理解如何在这种条件下提供准确和确定的结果是至关重要的。 更重要的是,流处理程序可以按原样处理事件制作的也应该能够处理相同的历史事件方式,从而实现离线分析甚至时间旅行分析。 当然,前提是我们的系统可以保存状态,因为可能有故障发生。到目前为止,我们看到的所有窗口类型在产生结果前都需要保存之前的数据。实际上,如果我们想计算任何指标,即使是简单的计数,我们也需要保存状态。考虑到流处理程序可能会运行几天,几个月甚至几年,我们需要确保状态可以在发生故障的情况下可靠地恢复。 并且即使程序崩溃,我们的系统也能保证计算出准确的结果。本章,我们将在流处理应用可能发生故障的语境下,深入探讨时间和状态的概念。
4 时间语义
在本节中,我们将介绍时间语义,并描述流中不同的时间概念。我们将讨论流处理器在乱序事件流的情况下如何提供准确的计算结果,以及我们如何处理历史事件流,如何在流中进行时间旅行。
4.1 在流处理中一分钟代表什么?
在处理可能是无限的事件流(包含了连续到达的事件),时间成为流处理程序的核心方面。假设我们想要连续的计算结果,可能每分钟就要计算一次。在我们的流处理程序上下文中,一分钟的意思是什么?
考虑一个程序需要分析一款移动端的在线游戏的用户所产生的事件流。游戏中的用户分了组,而应用程序将收集每个小组的活动数据,基于小组中的成员多快达到了游戏设定的目标,然后在游戏中提供奖励。例如额外的生命和用户升级。例如,如果一个小组中的所有用户在一分钟之内都弹出了500个泡泡,他们将升一级。Alice是一个勤奋的玩家,她在每天早晨的通勤时间玩游戏。问题在于Alice住在柏林,并且乘地铁去上班。而柏林的地铁手机信号很差。我们设想一个这样的场景,Alice当她的手机连上网时,开始弹泡泡,然后游戏会将数据发送到我们编写的应用程序中,这时地铁突然进入了隧道,她的手机也断网了。Alice还在玩这个游戏,而产生的事件将会缓存在手机中。当地铁离开隧道,Alice的手机又在线了,而手机中缓存的游戏事件将发送到应用程序。我们的应用程序应该如何处理这些数据?在这个场景中一分钟的意思是什么?这个一分钟应该包含Alice离线的那段时间吗?下图展示了这个问题。
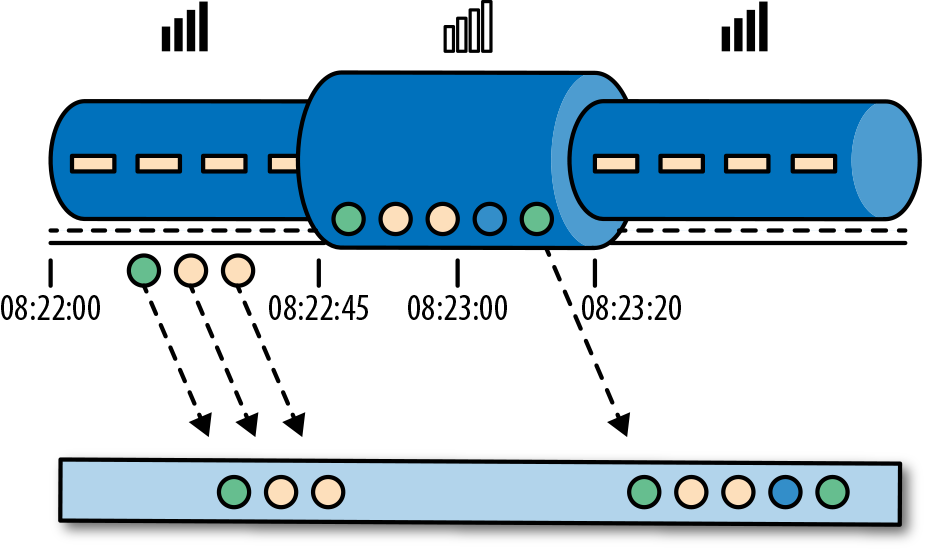
在线手游是一个简单的场景,展示了应用程序的运算应该取决于事件实际发生的时间,而不是应用程序收到事件的时间。如果我们按照应用程序收到事件的时间来进行处理的话,最糟糕的后果就是,Alice和她的朋友们再也不玩这个游戏了。但是还有很多时间语义非常关键的应用程序,我们需要保证时间语义的正确性。如果我们只考虑我们在一分钟之内收到了多少数据,我们的结果会变化,因为结果取决于网络连接的速度或处理的速度。相反,定义一分钟之内的事件数量,这个一分钟应该是数据本身的时间。
在Alice的这个例子中,流处理程序可能会碰到两个不同的时间概念:处理时间和事件时间。我们将在接下来的部分,讨论这两个概念。
4.2 处理时间
处理时间是处理流的应用程序的机器的本地时钟的时间(墙上时钟)。处理时间的窗口包含了一个时间段内来到机器的所有事件。这个时间段指的是机器的墙上时钟。如下图所示,在Alice的这个例子中,处理时间窗口在Alice的手机离线的情况下,时间将会继续行走。但这个处理时间窗口将不会收集Alice的手机离线时产生的事件。
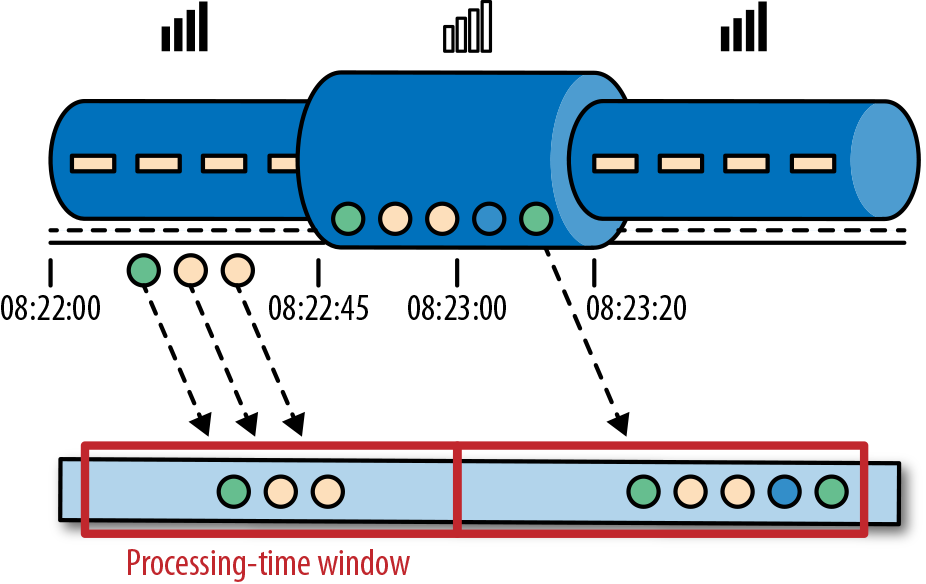
4.3 事件时间
事件时间是流中的事件实际发生的时间。事件时间基于流中的事件所包含的时间戳。通常情况下,在事件进入流处理程序前,事件数据就已经包含了时间戳。下图展示了事件时间窗口将会正确的将事件分发到窗口中去。可以如实反应事情是怎么发生的。即使事件可能存在延迟。
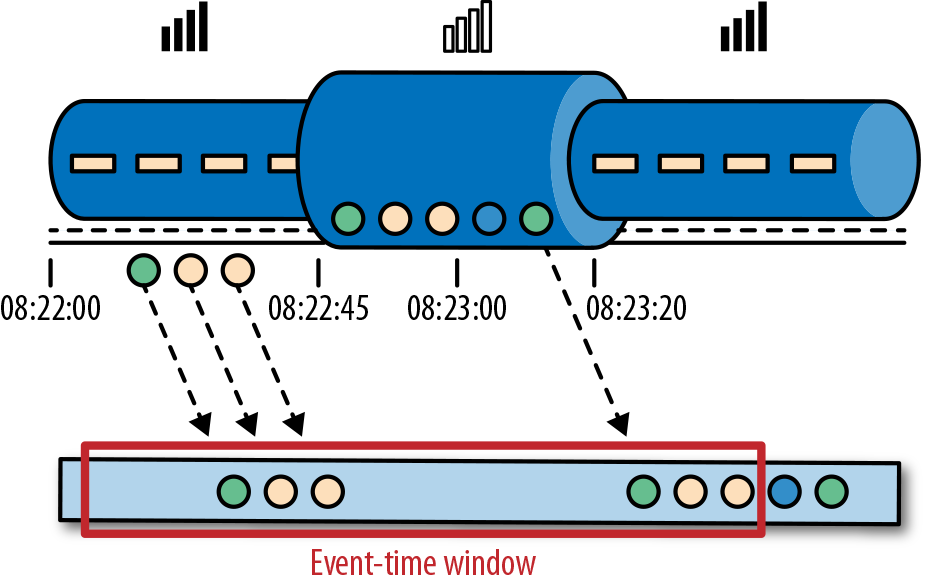
事件时间使得计算结果的过程不需要依赖处理数据的速度。基于事件时间的操作是可以预测的,而计算结果也是确定的。无论流处理程序处理流数据的速度快或是慢,无论事件到达流处理程序的速度快或是慢,事件时间窗口的计算结果都是一样的。
可以处理迟到的事件只是我们使用事件时间所克服的一个挑战而已。普遍存在的事件乱序问题可以使用事件时间得到解决。考虑和Alice玩同样游戏的Bob,他恰好和Alice在同一趟地铁上。Alice和Bob虽然玩的游戏一样,但他们的手机信号是不同的运营商提供的。当Alice的手机没信号时,Bob的手机依然有信号,游戏数据可以正常发送出去。
如果使用事件时间,即使碰到了事件乱序到达的情况,我们也可以保证结果的正确性。还有,当我们在处理可以重播的流数据时,由于时间戳的确定性,我们可以快进过去。也就是说,我们可以重播一条流,然后分析历史数据,就好像流中的事件是实时发生一样。另外,我们可以快进历史数据来使我们的应用程序追上现在的事件,然后应用程序仍然是一个实时处理程序,而且业务逻辑不需要改变。
4.4 水位线
在我们对事件时间窗口的讨论中,我们忽略了一个很重要的方面:我们应该怎样去决定何时触发事件时间窗口的计算?也就是说,在我们可以确定一个时间点之前的所有事件都已经到达之前,我们需要等待多久?我们如何知道事件是迟到的?在分布式系统无法准确预测行为的现实条件下,以及外部组件所引发的事件的延迟,以上问题并没有准确的答案。在本小节中,我们将会看到如何使用水位线来设置事件时间窗口的行为。
水位线是全局进度的度量标准。系统可以确信在一个时间点之后,不会有早于这个时间点发生的事件到来了。本质上,水位线提供了一个逻辑时钟,这个逻辑时钟告诉系统当前的事件时间。当一个运算符接收到含有时间T的水位线时,这个运算符会认为早于时间T的发生的事件已经全部都到达了。对于事件时间窗口和乱序事件的处理,水位线非常重要。运算符一旦接收到水位线,运算符会认为一段时间内发生的所有事件都已经观察到,可以触发针对这段时间内所有事件的计算了。
水位线提供了一种结果可信度和延时之间的妥协。激进的水位线设置可以保证低延迟,但结果的准确性不够。在这种情况下,迟到的事件有可能晚于水位线到达,我们需要编写一些代码来处理迟到事件。另一方面,如果水位线设置的过于宽松,计算的结果准确性会很高,但可能会增加流处理程序不必要的延时。
在很多真实世界的场景里面,系统无法获得足够的知识来完美的确定水位线。在手游这个场景中,我们无法得知一个用户离线时间会有多长,他们可能正在穿越一条隧道,可能正在乘飞机,可能永远不会再玩儿了。水位线无论是用户自定义的或者是自动生成的,在一个分布式系统中追踪全局的时间进度都不是很容易。所以仅仅依靠水位线可能并不是一个很好的主意。流处理系统还需要提供一些机制来处理迟到的元素(在水位线之后到达的事件)。根据应用场景,我们可能需要把迟到事件丢弃掉,或者写到日志里,或者使用迟到事件来更新之前已经计算好的结果。
4.5 处理时间和事件时间
大家可能会有疑问,既然事件时间已经可以解决我们的所有问题,为什么我们还要对比这两个时间概念?真相是,处理时间在很多情况下依然很有用。处理时间窗口将会带来理论上最低的延迟。因为我们不需要考虑迟到事件以及乱序事件,所以一个窗口只需要简单的缓存窗口内的数据即可,一旦机器时间超过指定的处理时间窗口的结束时间,就会触发窗口的计算。所以对于一些处理速度比结果准确性更重要的流处理程序,处理时间就派上用场了。另一个应用场景是,当我们需要在真实的时间场景下,周期性的报告结果时,同时不考虑结果的准确性。一个例子就是一个实时监控的仪表盘,负责显示当事件到达时立即聚合的结果。最后,处理时间窗口可以提供流本身数据的忠实表达,对于一些案例可能是很必要的特性。例如我们可能对观察流和对每分钟事件的计数(检测可能存在的停电状况)很感兴趣。简单的说,处理时间提供了低延迟,同时结果也取决于处理速度,并且也不能保证确定性。另一方面,事件时间保证了结果的确定性,同时还可以使我们能够处理迟到的或者乱序的事件流。
5 状态和持久化模型
我们现在转向另一个对于流处理程序非常重要的话题:状态。在数据处理中,状态是普遍存在的。任何稍微复杂一点的计算,都涉及到状态。为了产生计算结果,一个函数在一段时间内的一定数量的事件上来累加状态(例如,聚合计算或者模式匹配)。有状态的运算符使用输入的事件以及内部保存的状态来计算得到输出。例如,一个滚动聚合运算符需要输出这个运算符所观察到的所有事件的累加和。这个运算符将会在内部保存当前观察到的所有事件的累加和,同时每输入一个事件就更新一次累加和的计算结果。相似的,当一个运算符检测到一个“高温”事件紧接着十分钟以内检测到一个“烟雾”事件时,将会报警。直到运算符观察到一个“烟雾”事件或者十分钟的时间段已经过去,这个运算符需要在内部状态中一直保存着“高温”事件。
当我们考虑一下使用批处理系统来分析一个无界数据集时,会发现状态的重要性显而易见。在现代流处理器兴起之前,处理无界数据集的一个通常做法是将输入的事件攒成微批,然后交由批处理器来处理。当一个任务结束时,计算结果将被持久化,而所有的运算符状态就丢失了。一旦一个任务在计算下一个微批次的数据时,这个任务是无法访问上一个任务的状态的(都丢掉了)。这个问题通常使用将状态代理到外部系统(例如数据库)的方法来解决。相反,在一个连续不间断运行的流处理任务中,事件的状态是一直存在的,我们可以将状态暴露出来作为编程模型中的一等公民。当然,我们的确可以使用外部系统来管理流的状态,即使这个解决方案会带来额外的延迟。
由于流处理运算符默认处理的是无界数据流。所以我们必须要注意不要让内部状态无限的增长。为了限制状态的大小,运算符通常情况下会保存一些之前所观察到的事件流的总结或者概要。这个总结可能是一个计数值,一个累加和,或者事件流的采样,窗口的缓存操作,或者是一个自定义的数据结构,这个数据结构用来保存数据流中感兴趣的一些特性。
我们可以想象的到,支持有状态的运算符可能会碰到一些实现上的挑战:
状态管理
系统需要高效的管理状态,并保证针对状态的并发更新,不会产生竞争条件(race condition)。
状态分区
并行会带来复杂性。因为计算结果同时取决于已经保存的状态和输入的事件流。幸运的是,大多数情况下,我们可以使用Key来对状态进行分区,然后独立的管理每一个分区。例如,当我们处理一组传感器的测量事件流时,我们可以使用分区的运算符状态来针对不同的传感器独立的保存状态。
状态恢复
第三个挑战是有状态的运算符如何保证状态可以恢复,即使出现任务失败的情况,计算也是正确的。
下一节,我们将讨论任务失败和计算结果的保证。
5.1 任务失败
流任务中的运算符状态是很宝贵的,也需要抵御任务失败带来的问题。如果在任务失败的情况下,状态丢失的话,在任务恢复以后计算的结果将是不正确的。流任务会连续不断的运行很长时间,而状态可能已经收集了几天甚至几个月。在失败的情况下,重新处理所有的输入并重新生成一个丢失的状态,将会很浪费时间,开销也很大。
在本章开始时,我们看到如何将流的编程建模成数据流模型。在执行之前,流程序将会被翻译成物理层数据流图,物理层数据流图由连接的并行任务组成,而一个并行任务运行一些运算符逻辑,消费输入流数据,并为其他任务产生输出流数据。真实场景下,可能有数百个这样的任务并行运行在很多的物理机器上。在长时间的运行中,流任务中的任意一个任务在任意时间点都有可能失败。我们如何保证任务的失败能被正确的处理,以使任务能继续的运行下去呢?事实上,我们可能希望我们的流处理器不仅能在任务失败的情况下继续处理数据,还能保证计算结果的正确性以及运算符状态的安全。我们在本小节来讨论这些问题。
什么是任务失败?
对于流中的每一个事件,一个处理任务分为以下步骤:
(1)接收事件,并将事件存储在本地的缓存中;
(2)可能会更新内部状态;
(3)产生输出记录。这些步骤都能失败,而系统必须对于在失败的场景下如何处理有清晰的定义。如果任务在第一步就失败了,事件会丢失吗?如果当更新内部状态的时候任务失败,那么内部状态会在任务恢复以后更新吗?在以上这些场景中,输出是确定性的吗?
在批处理场景下,所有的问题都不是问题。因为我们可以很方便的重新计算。所以不会有事件丢失,状态也可以得到完全恢复。在流的世界里,处理失败不是一个小问题。流系统在失败的情况下需要保证结果的准确性。接下来,我们需要看一下现代流处理系统所提供的一些保障,以及实现这些保障的机制。
结果的保证
当我们讨论保证计算的结果时,我们的意思是流处理器的内部状态需要保证一致性。也就是说我们关心的是应用程序的代码在故障恢复以后看到的状态值是什么。要注意保证应用程序状态的一致性并不是保证应用程序的输出结果的一致性。一旦输出结果被持久化,结果的准确性就很难保证了。除非持久化系统支持事务。
AT-MOST-ONCE
当任务故障时,最简单的做法是什么都不干,既不恢复丢失的状态,也不重播丢失的事件。At-most-once语义的含义是最多处理一次事件。换句话说,事件可以被丢弃掉,也没有任何操作来保证结果的准确性。这种类型的保证也叫“没有保证”,因为一个丢弃掉所有事件的系统其实也提供了这样的保障。没有保障听起来是一个糟糕的主意,但如果我们能接受近似的结果,并且希望尽可能低的延迟,那么这样也挺好。
AT-LEAST-ONCE
在大多数的真实应用场景,我们希望不丢失事件。这种类型的保障成为at-least-once,意思是所有的事件都得到了处理,而且一些事件还可能被处理多次。如果结果的正确性仅仅依赖于数据的完整性,那么重复处理是可以接受的。例如,判断一个事件是否在流中出现过,at-least-once这样的保证完全可以正确的实现。在最坏的情况下,我们多次遇到了这个事件。而如果我们要对一个特定的事件进行计数,计算结果就可能是错误的了。
为了保证在at-least-once语义的保证下,计算结果也能正确。我们还需要另一套系统来从数据源或者缓存中重新播放数据。持久化的事件日志系统将会把所有的事件写入到持久化存储中。所以如果任务发生故障,这些数据可以重新播放。还有一种方法可以获得同等的效果,就是使用结果承认机制。这种方法将会把每一条数据都保存在缓存中,直到数据的处理等到所有的任务的承认。一旦得到所有任务的承认,数据将被丢弃。
EXACTLY-ONCE
恰好处理一次是最严格的保证,也是最难实现的。恰好处理一次语义不仅仅意味着没有事件丢失,还意味着针对每一个数据,内部状态仅仅更新一次。本质上,恰好处理一次语义意味着我们的应用程序可以提供准确的结果,就好像从未发生过故障。
提供恰好处理一次语义的保证必须有至少处理一次语义的保证才行,同时还需要数据重放机制。另外,流处理器还需要保证内部状态的一致性。也就是说,在故障恢复以后,流处理器应该知道一个事件有没有在状态中更新。事务更新是达到这个目标的一种方法,但可能引入很大的性能问题。Flink使用了一种轻量级快照机制来保证恰好处理一次语义。
端到端恰好处理一次
目前我们看到的一致性保证都是由流处理器实现的,也就是说都是在Flink流处理器内部保证的。而在真实世界中,流处理应用除了流处理器以外还包含了数据源(例如Kafka)和持久化系统。端到端的一致性保证意味着结果的正确性贯穿了整个流处理应用的始终。每一个组件都保证了它自己的一致性。而整个端到端的一致性级别取决于所有组件中一致性最弱的组件。要注意的是,我们可以通过弱一致性来实现更强的一致性语义。例如,当任务的操作具有幂等性时,比如流的最大值或者最小值的计算。在这种场景下,我们可以通过最少处理一次这样的一致性来实现恰好处理一次这样的最高级别的一致性。