1 气泡图
气泡图和上面的散点图非常类似,只是点的大小不一样,而且是通过参数 s 来进行控制的,多的不说,还是看个示例:
例子一:
import matplotlib.pyplot as plt import numpy as np # 处理中文乱码 plt.rcParams['font.sans-serif']=['SimHei'] x_data = np.array([2011,2012,2013,2014,2015,2016,2017]) y_data = np.array([58000,60200,63000,71000,84000,90500,107000]) # 根据 y 值的不同生成不同的颜色 colors = y_data * 10 # 根据 y 值的不同生成不同的大小 area = y_data / 300 plt.scatter(x_data, y_data, s = area, c = colors, marker='o', edgecolor='black', alpha=0.5, label = '产品销量') plt.legend() plt.savefig("scatter_demo1.png")
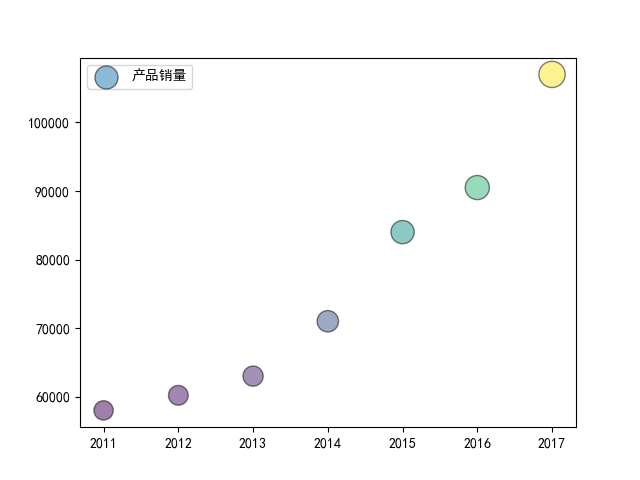
例子二:
import numpy as np import matplotlib.pyplot as plt import matplotlib.cbook as cbook # Load a numpy record array from yahoo csv data with fields date, open, close, # volume, adj_close from the mpl-data/example directory. The record array # stores the date as an np.datetime64 with a day unit ('D') in the date column. with cbook.get_sample_data('goog.npz') as datafile: price_data = np.load(datafile)['price_data'].view(np.recarray) price_data = price_data[-250:] # get the most recent 250 trading days delta1 = np.diff(price_data.adj_close) / price_data.adj_close[:-1] # Marker size in units of points^2 volume = (15 * price_data.volume[:-2] / price_data.volume[0])**2 close = 0.003 * price_data.close[:-2] / 0.003 * price_data.open[:-2] fig, ax = plt.subplots() ax.scatter(delta1[:-1], delta1[1:], c=close, s=volume, alpha=0.5) ax.set_xlabel(r'$Delta_i$', fontsize=15) ax.set_ylabel(r'$Delta_{i+1}$', fontsize=15) ax.set_title('Volume and percent change') ax.grid(True) fig.tight_layout() plt.show()

堆叠图
堆叠图的作用和折线图非常类似,它采用的是 stackplot() 方法。
plt.stackplot(x, y, labels, colors)
import matplotlib.pyplot as plt # 处理中文乱码 plt.rcParams['font.sans-serif']=['SimHei'] x_data = [2011,2012,2013,2014,2015,2016,2017] y_data = [58000,60200,63000,71000,84000,90500,107000] y_data_1 = [78000,80200,93000,101000,64000,70500,87000] plt.title(label='xxx 公司 xxx 产品销量') plt.stackplot(x_data, y_data, y_data_1, labels=['产品销量', '用户增长数']) plt.legend() plt.savefig("stackplot_demo.png")
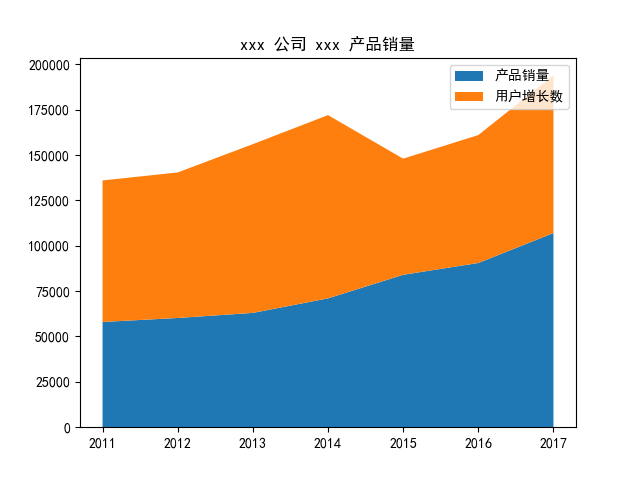
例子二:
import numpy as np import matplotlib.pyplot as plt x = [1, 2, 3, 4, 5] y1 = [1, 1, 2, 3, 5] y2 = [0, 4, 2, 6, 8] y3 = [1, 3, 5, 7, 9] y = np.vstack([y1, y2, y3]) labels = ["Fibonacci ", "Evens", "Odds"] fig, ax = plt.subplots() ax.stackplot(x, y1, y2, y3, labels=labels) ax.legend(loc='upper left') plt.show()
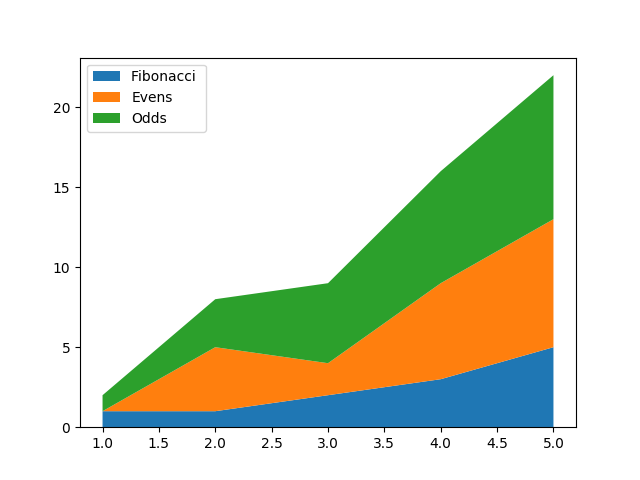
雷达图
它可以直观的看出来一个事物的优势与不足。
在 plt 中建立雷达图是用 polar() 方法的,这个方法其实是用来建立极坐标系的,而雷达图就是先在极坐标系中将各个点找出来,然后再将他们连线连起来。
plt.polar(theta, r, **kwargs)
- theta : 每一个点在极坐标系中的角度
- r : 每一个点在极坐标系中的半径
import numpy as np import matplotlib.pyplot as plt # 中文和负号的正常显示 plt.rcParams['font.sans-serif']=['SimHei'] plt.rcParams['axes.unicode_minus'] = False # 使用ggplot的绘图风格 plt.style.use('ggplot') # 构造数据 values = [3.2, 2.1, 3.5, 2.8, 3] feature = ['攻击力', '防御力', '恢复力', '法术强度', '生命值'] N = len(values) # 设置雷达图的角度,用于平分切开一个圆面 angles = np.linspace(0, 2 * np.pi, N, endpoint=False) # 为了使雷达图一圈封闭起来,需要下面的步骤 values = np.concatenate((values, [values[0]])) angles = np.concatenate((angles, [angles[0]])) # 绘图 fig = plt.figure() # 这里一定要设置为极坐标格式 ax = fig.add_subplot(111, polar=True) # 绘制折线图 ax.plot(angles, values, 'o-', linewidth=2) # 填充颜色 ax.fill(angles, values, alpha=0.25) # 添加每个特征的标签 ax.set_thetagrids(angles * 180 / np.pi, feature) # 设置雷达图的范围 ax.set_ylim(0, 5) # 添加标题 plt.title('游戏人物属性') # 添加网格线 ax.grid(True) # 显示图形 plt.savefig('polar_demo.png')
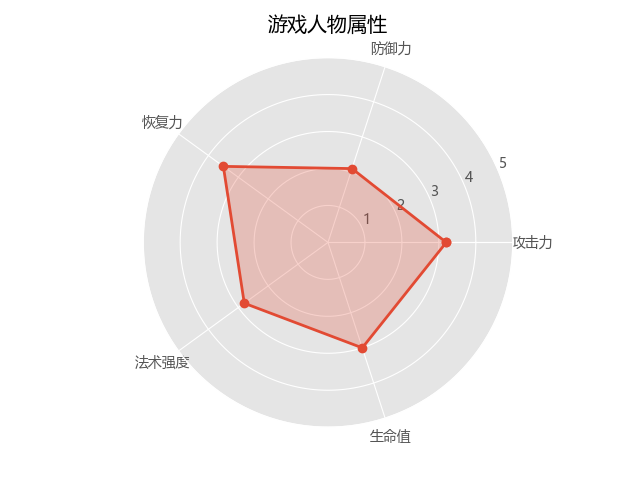
例子二
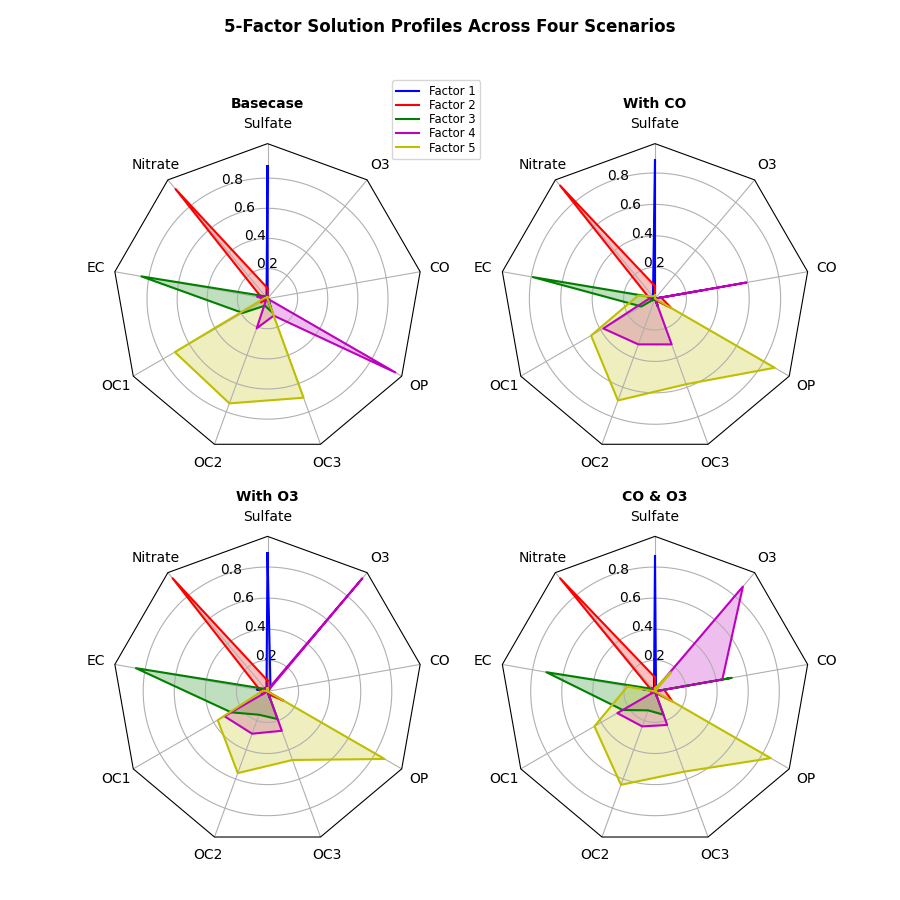
import numpy as np import matplotlib.pyplot as plt from matplotlib.patches import Circle, RegularPolygon from matplotlib.path import Path from matplotlib.projections.polar import PolarAxes from matplotlib.projections import register_projection from matplotlib.spines import Spine from matplotlib.transforms import Affine2D def radar_factory(num_vars, frame='circle'): """Create a radar chart with `num_vars` axes. This function creates a RadarAxes projection and registers it. Parameters ---------- num_vars : int Number of variables for radar chart. frame : {'circle', 'polygon'} Shape of frame surrounding axes. """ # calculate evenly-spaced axis angles theta = np.linspace(0, 2*np.pi, num_vars, endpoint=False) class RadarAxes(PolarAxes): name = 'radar' # use 1 line segment to connect specified points RESOLUTION = 1 def __init__(self, *args, **kwargs): super().__init__(*args, **kwargs) # rotate plot such that the first axis is at the top self.set_theta_zero_location('N') def fill(self, *args, closed=True, **kwargs): """Override fill so that line is closed by default""" return super().fill(closed=closed, *args, **kwargs) def plot(self, *args, **kwargs): """Override plot so that line is closed by default""" lines = super().plot(*args, **kwargs) for line in lines: self._close_line(line) def _close_line(self, line): x, y = line.get_data() # FIXME: markers at x[0], y[0] get doubled-up if x[0] != x[-1]: x = np.concatenate((x, [x[0]])) y = np.concatenate((y, [y[0]])) line.set_data(x, y) def set_varlabels(self, labels): self.set_thetagrids(np.degrees(theta), labels) def _gen_axes_patch(self): # The Axes patch must be centered at (0.5, 0.5) and of radius 0.5 # in axes coordinates. if frame == 'circle': return Circle((0.5, 0.5), 0.5) elif frame == 'polygon': return RegularPolygon((0.5, 0.5), num_vars, radius=.5, edgecolor="k") else: raise ValueError("unknown value for 'frame': %s" % frame) def _gen_axes_spines(self): if frame == 'circle': return super()._gen_axes_spines() elif frame == 'polygon': # spine_type must be 'left'/'right'/'top'/'bottom'/'circle'. spine = Spine(axes=self, spine_type='circle', path=Path.unit_regular_polygon(num_vars)) # unit_regular_polygon gives a polygon of radius 1 centered at # (0, 0) but we want a polygon of radius 0.5 centered at (0.5, # 0.5) in axes coordinates. spine.set_transform(Affine2D().scale(.5).translate(.5, .5) + self.transAxes) return {'polar': spine} else: raise ValueError("unknown value for 'frame': %s" % frame) register_projection(RadarAxes) return theta def example_data(): # The following data is from the Denver Aerosol Sources and Health study. # See doi:10.1016/j.atmosenv.2008.12.017 # # The data are pollution source profile estimates for five modeled # pollution sources (e.g., cars, wood-burning, etc) that emit 7-9 chemical # species. The radar charts are experimented with here to see if we can # nicely visualize how the modeled source profiles change across four # scenarios: # 1) No gas-phase species present, just seven particulate counts on # Sulfate # Nitrate # Elemental Carbon (EC) # Organic Carbon fraction 1 (OC) # Organic Carbon fraction 2 (OC2) # Organic Carbon fraction 3 (OC3) # Pyrolized Organic Carbon (OP) # 2)Inclusion of gas-phase specie carbon monoxide (CO) # 3)Inclusion of gas-phase specie ozone (O3). # 4)Inclusion of both gas-phase species is present... data = [ ['Sulfate', 'Nitrate', 'EC', 'OC1', 'OC2', 'OC3', 'OP', 'CO', 'O3'], ('Basecase', [ [0.88, 0.01, 0.03, 0.03, 0.00, 0.06, 0.01, 0.00, 0.00], [0.07, 0.95, 0.04, 0.05, 0.00, 0.02, 0.01, 0.00, 0.00], [0.01, 0.02, 0.85, 0.19, 0.05, 0.10, 0.00, 0.00, 0.00], [0.02, 0.01, 0.07, 0.01, 0.21, 0.12, 0.98, 0.00, 0.00], [0.01, 0.01, 0.02, 0.71, 0.74, 0.70, 0.00, 0.00, 0.00]]), ('With CO', [ [0.88, 0.02, 0.02, 0.02, 0.00, 0.05, 0.00, 0.05, 0.00], [0.08, 0.94, 0.04, 0.02, 0.00, 0.01, 0.12, 0.04, 0.00], [0.01, 0.01, 0.79, 0.10, 0.00, 0.05, 0.00, 0.31, 0.00], [0.00, 0.02, 0.03, 0.38, 0.31, 0.31, 0.00, 0.59, 0.00], [0.02, 0.02, 0.11, 0.47, 0.69, 0.58, 0.88, 0.00, 0.00]]), ('With O3', [ [0.89, 0.01, 0.07, 0.00, 0.00, 0.05, 0.00, 0.00, 0.03], [0.07, 0.95, 0.05, 0.04, 0.00, 0.02, 0.12, 0.00, 0.00], [0.01, 0.02, 0.86, 0.27, 0.16, 0.19, 0.00, 0.00, 0.00], [0.01, 0.03, 0.00, 0.32, 0.29, 0.27, 0.00, 0.00, 0.95], [0.02, 0.00, 0.03, 0.37, 0.56, 0.47, 0.87, 0.00, 0.00]]), ('CO & O3', [ [0.87, 0.01, 0.08, 0.00, 0.00, 0.04, 0.00, 0.00, 0.01], [0.09, 0.95, 0.02, 0.03, 0.00, 0.01, 0.13, 0.06, 0.00], [0.01, 0.02, 0.71, 0.24, 0.13, 0.16, 0.00, 0.50, 0.00], [0.01, 0.03, 0.00, 0.28, 0.24, 0.23, 0.00, 0.44, 0.88], [0.02, 0.00, 0.18, 0.45, 0.64, 0.55, 0.86, 0.00, 0.16]]) ] return data if __name__ == '__main__': N = 9 theta = radar_factory(N, frame='polygon') data = example_data() spoke_labels = data.pop(0) fig, axs = plt.subplots(figsize=(9, 9), nrows=2, ncols=2, subplot_kw=dict(projection='radar')) fig.subplots_adjust(wspace=0.25, hspace=0.20, top=0.85, bottom=0.05) colors = ['b', 'r', 'g', 'm', 'y'] # Plot the four cases from the example data on separate axes for ax, (title, case_data) in zip(axs.flat, data): ax.set_rgrids([0.2, 0.4, 0.6, 0.8]) ax.set_title(title, weight='bold', size='medium', position=(0.5, 1.1), horizontalalignment='center', verticalalignment='center') for d, color in zip(case_data, colors): ax.plot(theta, d, color=color) ax.fill(theta, d, facecolor=color, alpha=0.25) ax.set_varlabels(spoke_labels) # add legend relative to top-left plot labels = ('Factor 1', 'Factor 2', 'Factor 3', 'Factor 4', 'Factor 5') legend = axs[0, 0].legend(labels, loc=(0.9, .95), labelspacing=0.1, fontsize='small') fig.text(0.5, 0.965, '5-Factor Solution Profiles Across Four Scenarios', horizontalalignment='center', color='black', weight='bold', size='large') plt.show()
饼图
matplotlib.pyplot.pie(
x, explode=None, labels=None, colors=None,
autopct=None, pctdistance=0.6, shadow=False,
labeldistance=1.1, startangle=None, radius=None,
counterclock=True, wedgeprops=None, textprops=None,
center=(0, 0), frame=False, hold=None, data=None)
- x : array-like
- explode : array-like, optional, default: None(设置饼图偏离)
- labels : list, optional, default: None(标签)
- colors : array-like, optional, default: None(颜色设置)
- autopct : None (default), string, or function, optional(设置百分比显示)
- pctdistance : float, optional, default: 0.6(百分比距圆心的位置)
- shadow : bool, optional, default: False(设置阴影)
- labeldistance : float, optional, default: 1.1(标签距圆心的距离)
- startangle : float, optional, default: None(开始位置的旋转角度,第一个分类是在右45度位置)
- radius : float, optional, default: None(设置半径的大小)
- counterclock : bool, optional, default: True(是否逆时针)
- wedgeprops : dict, optional, default: None(内外边界设置)
- textprops : dict, optional, default: None(文本设置)
- center : list of float, optional, default: (0, 0)(设置中心位置)
- frame : bool, optional, default: False(是否显示饼图背后图框)
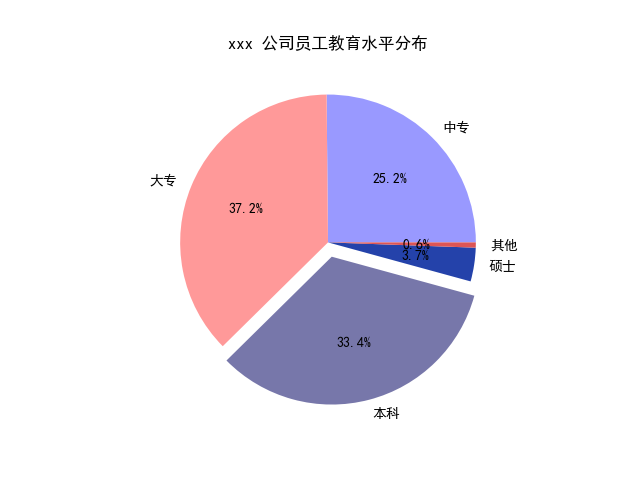
import matplotlib.pyplot as plt # 中文和负号的正常显示 plt.rcParams['font.sans-serif']=['SimHei'] plt.rcParams['axes.unicode_minus'] = False # 数据 edu = [0.2515,0.3724,0.3336,0.0368,0.0057] labels = ['中专','大专','本科','硕士','其他'] # 让本科学历离圆心远一点 explode = [0,0,0.1,0,0] # 将横、纵坐标轴标准化处理,保证饼图是一个正圆,否则为椭圆 plt.axes(aspect='equal') # 自定义颜色 colors=['#9999ff','#ff9999','#7777aa','#2442aa','#dd5555'] # 自定义颜色 # 绘制饼图 plt.pie(x=edu, # 绘图数据 explode = explode, # 突出显示大专人群 labels = labels, # 添加教育水平标签 colors = colors, # 设置饼图的自定义填充色 autopct = '%.1f%%', # 设置百分比的格式,这里保留一位小数 ) # 添加图标题 plt.title('xxx 公司员工教育水平分布') # 保存图形 plt.savefig('pie_demo.png')
例子二
import numpy as np import matplotlib.pyplot as plt fig, ax = plt.subplots(figsize=(6, 3), subplot_kw=dict(aspect="equal")) recipe = ["375 g flour", "75 g sugar", "250 g butter", "300 g berries"] data = [float(x.split()[0]) for x in recipe] ingredients = [x.split()[-1] for x in recipe] def func(pct, allvals): absolute = int(pct/100.*np.sum(allvals)) return "{:.1f}% ({:d} g)".format(pct, absolute) wedges, texts, autotexts = ax.pie(data, autopct=lambda pct: func(pct, data), textprops=dict(color="w")) ax.legend(wedges, ingredients, title="Ingredients", loc="center left", bbox_to_anchor=(1, 0, 0.5, 1)) plt.setp(autotexts, size=8, weight="bold") ax.set_title("Matplotlib bakery: A pie") plt.show()
