1 色比色差定律
在前面的博客<图像bayer格式介绍以及bayer插值原理CFA>中,简单介绍了Bayer域插值原理以及早期常用的双线性插值算法。双线性插值算法的优点是原理简单,实现相对容易,性能较高,占用硬件资源较少,但是在图像RGB恢复过程中会造成边缘信息的丢失和模糊,另外由于没有考虑颜色通道之间相关性,因此图像恢复主观视觉效果差,容易产生锯齿效应。鉴于双线性插值算法的缺点,优化锯齿效应,新的算法需要考虑RGB通道色彩相关性。
蒙德里安(Mondriann)彩色图像的成像模型:每个颜色通道可以被看作真实三维世界的表面法向量n(x)在光源方向了的投影与反射率p(x,y)的乘积。反射率p(x,y)表征了三维物体的材料特性,并且不同颜色的反射率是互不相同的。根据该模型,红、绿和蓝三色通道可由下列公式表示:
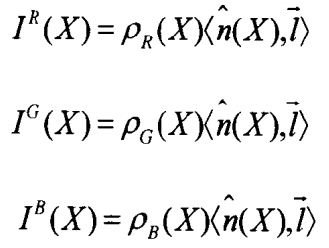
根据上述公式,假设图片中的一个给定物体的材料是相同的,即材料对于红色、蓝色和绿色的反射率在给定物体范围内固定不变,即p(X)=c。可以推导以下比值关系 :
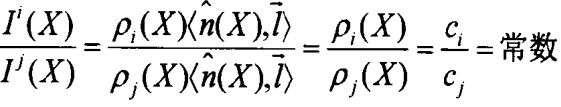
由上可知,在给定的物体内的任一位置,颜色比值为常量。虽然上述比值关系基于简单的假设条件,但在图像的小块局部邻域内,且该局部邻域没有横越图像边缘的情况下,仍是有效的,符合自然图像色彩亮度均匀过度这一特性。上述比值定律被称为色比定律。
色比定律是在线性曝光空间中讨论的得出的,将线性曝光空间的色比定律转换到对数曝光空间即可得到色差定律。色差定律可表达为,在图像的小范围局部邻域内I(i,x) - I(j,X)=常数。
常见Bayer域R/G/B分布模型如下,后续插值算法使用:
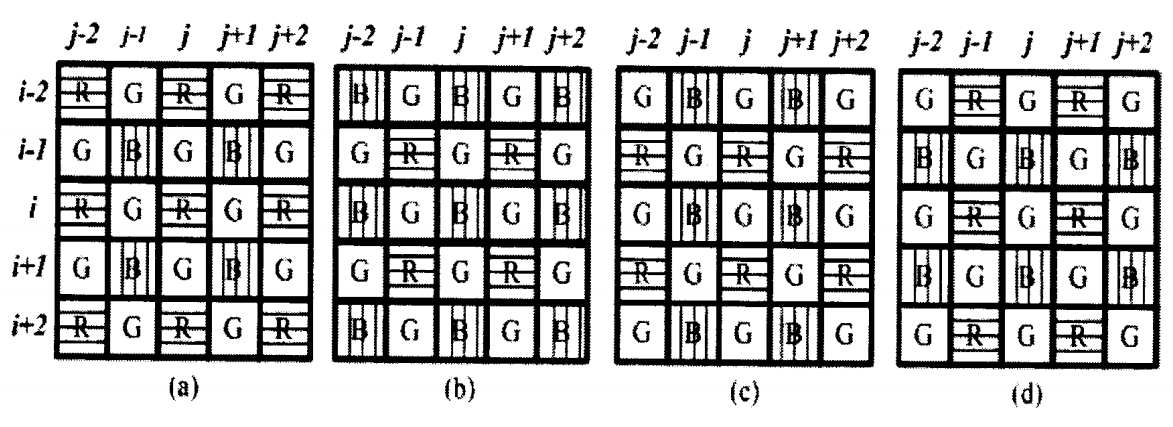
2 基于色比定律的插值算法
基色比定律的去马赛克算法,解决双线性插值过程中出现的不自然的色调变化情况。Bayer CFA可看作由亮度信号(高采样率的绿色像素点)和色度信号(低采样率的红色和蓝色像素点)组成。亮度信号可通过简单的双线性插值进行估算,色度信号通过应用邻域内的色调的平缓性来插值恢复。色调(hue)被定义为色度信号与亮度信号的比值,即蓝色采样点处的色调为B/G,红色采样点处的色调为R/G。 重建步骤如下:
(1) 用双线性插值算法恢复出红色和蓝色采样点处的绿色分量,图a/b为例如下:
(2) 使用已经重建好的绿色分量,基于色比定律恢复红色和蓝色分量,如图a红色采样点处的蓝色分量恢复策略如下,图b蓝色采样点处的红色分量恢复策略类似。在3*3中心领域内,基于色比定律可知:
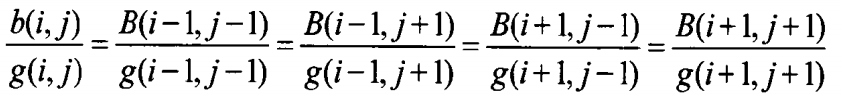
换算可得:
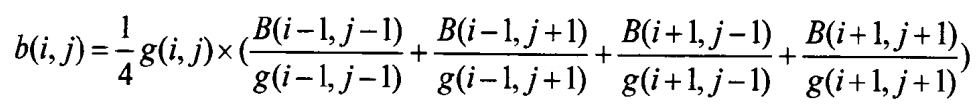
图c和图d中心绿色采样点处红色和蓝色分量的恢复方法相同,以图c为例,R/B恢复方法如下:
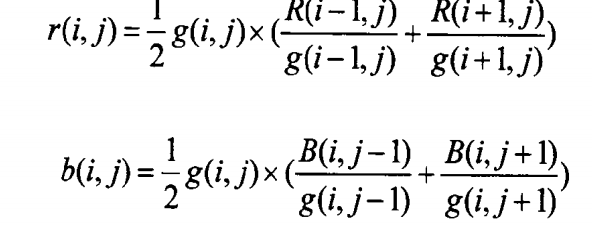
基于色比定律进行色比定律进行去马赛克操作需要涉及大量的乘法和除法操作,当某点的绿色分量为0时,还需要重新定义色调(Hue)的含义,因此算法实现时需要消耗大量的性能资源和条件保护。
3 基于色差定律的插值算法
基于色比定律实现的插值算法带来的缺陷性,运用如下的色差定律使得去马赛克设计的操作更加简单方便,运用色差定律时,色调(Hue)被定义为色度信号与亮度信号的差,即(B - G或R - G), 算法实现步骤如下:
(1) 用双线性插值恢复红色和蓝色采样点处丢失的绿色分量,同色比定律的绿色分量恢复;
(2) 用已经恢复的绿色分量,基于色差定律,恢复图(a)和图(b)中的蓝色或红色分量,具体如下: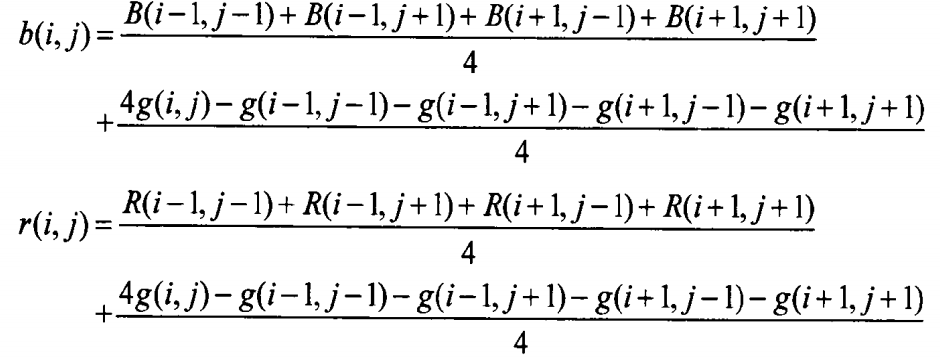 (3) 用已经恢复的绿色分量,基于色差定律,恢复图c和图d中的蓝色和红色分量,以图c为例,如下:
(3) 用已经恢复的绿色分量,基于色差定律,恢复图c和图d中的蓝色和红色分量,以图c为例,如下:
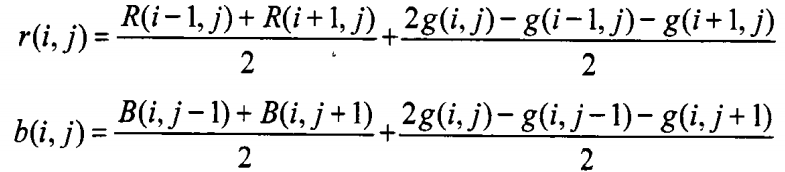
相对于基于色比定律的色差算法,利用色差定律的插值算法仅仅通过加减法和移位操作即可完成,计算开销非常小,易于硬件化,在性能和硬件资源消耗上明显优于前者。
4 算法优缺点
基于色差色比定律的去马赛克算法虽然利用了颜色空间的相关性进行插值,其本质还是3x3邻域内的双线性插值。因为绿色.分量的插值运算仍然基于双线,因此会存在如下现象:
(1) 当该3x3邻域内的色彩值较为接近,即为图像平滑区域,无边缘相交时,可取的较好的插值效果;
(2) 当处于边缘地带时,由于绿色分量的插值不包含边缘信息,且错误的绿色分量会进而影响红色蓝色分量的插值重建,图像会产生很多错误颜色;
针对该现象,后续会陆续介绍进一步优化后的CFA插值算法。