示例 1:
输入:[1,2,3,4,5,6,7]和 k = 3 输出:[5,6,7,1,2,3,4]解释: 向右旋转 1 步:[7,1,2,3,4,5,6]向右旋转 2 步:[6,7,1,2,3,4,5]向右旋转 3 步:[5,6,7,1,2,3,4]
示例 2:
输入: [-1,-100,3,99] 和 k = 2
输出: [3,99,-1,-100]
解释:
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]
说明:
- 尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。
- 要求使用空间复杂度为 O(1) 的原地算法。
——————————————————————————————————————————————
1. 暴力模拟,O(n*k),TLE:
1 class Solution(object): 2 def rotate(self, nums, k): 3 """ 4 :type nums: List[int] 5 :type k: int 6 :rtype: void Do not return anything, modify nums in-place instead. 7 """ 8 extraLattice = 0 9 arrLen = len(nums) 10 11 if arrLen > 0: 12 for i in range(0, k): 13 extraLattice = nums[arrLen-1] 14 for j in range(arrLen-2, -1, -1): 15 nums[j+1] = nums[j] 16 nums[0] = extraLattice
2. 考虑到数组元素可以随机访问,而且本题中根据数组元素的原始下标可以计算出目标下标,所以想了很久如何通过整体移动数组分段来达到目标状态,然后把分段细化为单个数组元素以减少临时存储空间。但是发现并不可行,因为如果不想引入额外的大块存储空间,只能使用swich的方式顺序地交换每两个数组元素且仅交换一次,这种方法的关键是找到一个合理的分治顺序,但理论上可能交换数组之间成环(swich_a_b, swich_b_a 或者 swich_a_b, swich_b_c, swich_c_a)且可能很难判断是否成环,成环后重复交换违反仅交换一次的原则也不能跳出去交换其他数组元素。如果引入额外的标记数组也很难写逻辑。这样思路就被导向使用等长的额外存储数组保存待交换的分段。因此“分段”的思想有点坑,遂放弃之。
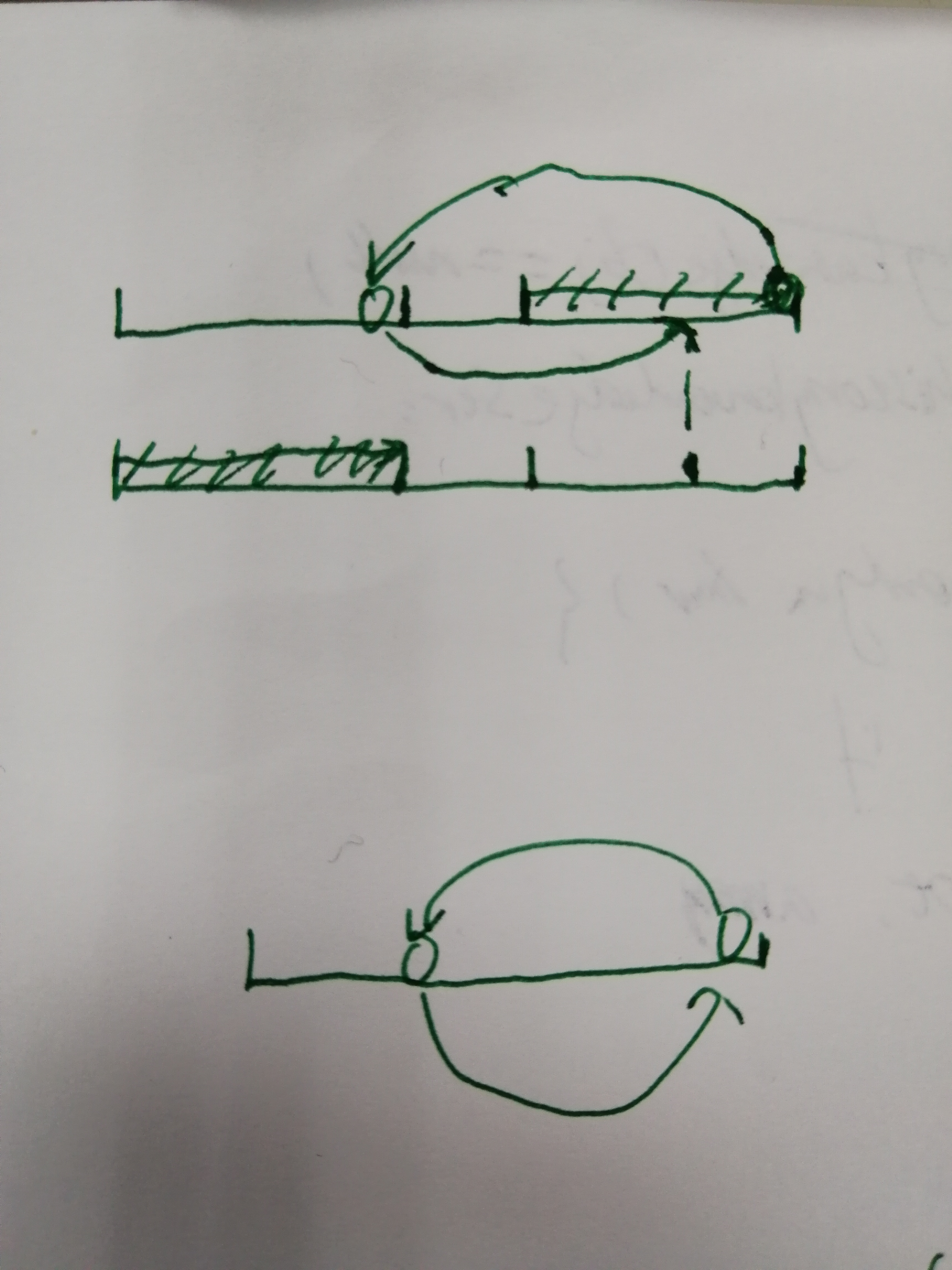
3. 随后我感觉到分段思想的特点是分段内部的顺序性,这导致分段必须被顺序存储到一个额外的存储空间以保持其内部顺序性,本质上这种想法还是很朴素的定义在分段上的“三行交换”。遂想到找一种新的交换方法,打破这种“分段的内部顺序性”,通过一些跨越分段内部和外部的方法,原地转置数组,但能保证有序可以恢复顺序。遂想到最简单的“就地逆置”方法,将数组分为两段之后各自逆置,然后整体逆置前后较短分段长度,然后逆置剩余部分。两次逆置(分段逆置和整体逆置,打破了分段的顺序封闭性)之后恢复了数组分段的顺序,也将需要变换位置的前后两个部分转移到了各自的位置。最后一次逆置的分段的整体位置没有改变,但是也经历了两次逆置,其中第一次逆置将较长分段中的需要与较短分段交换位置的部分转换到相应待转换位置,第二次逆置恢复了原顺序。
这个思路的形成有理性的成分,但是想到的方法一次成功有很大的随机性,算是很幸运。
附AC代码:
1 class Solution(object): 2 def rotate(self, nums, k): 3 """ 4 :type nums: List[int] 5 :type k: int 6 :rtype: void Do not return anything, modify nums in-place instead. 7 """ 8 9 arrLen = len(nums) 10 11 ## reverse first segment 12 begin = 0 13 end = arrLen-k%arrLen-1 14 while begin < end: 15 temp = nums[begin] 16 nums[begin] = nums[end] 17 nums[end] = temp 18 begin += 1 19 end -= 1 20 21 ## reverse second segment 22 begin = arrLen-k%arrLen 23 end = arrLen-1 24 while begin < end: 25 temp = nums[begin] 26 nums[begin] = nums[end] 27 nums[end] = temp 28 begin += 1 29 end -= 1 30 31 ## revese whole arr 32 begin = 0 33 end = arrLen-1 34 while begin < end and begin < arrLen-k%arrLen and end > k%arrLen-1: 35 temp = nums[begin] 36 nums[begin] = nums[end] 37 nums[end] = temp 38 begin += 1 39 end -= 1 40 41 begin = arrLen-k%arrLen 42 end = k%arrLen-1 43 while begin < end: 44 temp = nums[begin] 45 nums[begin] = nums[end] 46 nums[end] = temp 47 begin += 1 48 end -= 1