• 《挑战程序设计竞赛》学习笔记 （1）

    2.2 贪心法

    • 贪心法是遵循某种规则，不断贪心选取当前最优策略的算法设计方法。
      • 贪心法的求解思想是通过迭代地选取当前问题的局部最优解法来达成总体最优解，在迭代的过程中不断地产生局部最优解和下一个与之前问题同构的子问题。
      • 贪心法所处理的问题总是具有最优子结构的性质：该问题的最优解包含子问题的最优解。
      • 使用贪心法处理的时候如何选取贪心策略非常关键，选定正确的策略往往要求一定的洞察力，验证贪心策略的正确性可能使用数学归纳法或者反证法。
      • 与搜索和动规不同，贪心法的特点是解决问题的顺序是固定的，而且不能回退。证明贪心策略在整体逻辑上一部分是为了证明贪心策略所确定的解题顺序是否可以保证得到整体最优解，但是在具体的问题中这种目的可能不是那么明显。
    • 例题
      • 硬币问题——入门：与搜索和动态规划不同，贪心法遵循某种规则，不断选取当前最优策略。注意结合题目中硬币面额他考虑贪心策略
      • 区间调度问题——开始涉及贪心策略的差异，尝试证明，☀专栏
      • 字典序最小问题（POJ3617）——理清思路，了解解题的一般方法
      • 其他问题之 Saruman's Army：较易
      • 其他问题之☀Fence Repair：了解自顶向下/自底向上的解决思路，强化解题的一般方法（此题自己想了一下，思路还算清楚，可以记录下来供以后参考）
    • 练习题（page135）
      • 区间
        • POJ 2376：Clean Shifts（AC）
           1 #include <iostream>
 2 #include <stdio.h>
 3 #include <algorithm>
 4 #include <vector>
 5 using namespace std;
 6 
 7 const int maxn = 25005;
 8 
 9 struct COW
10 {
11     int begin,end;
12 };
13 
14 bool cmp(COW a, COW b)
15 {
16     if(a.begin==b.begin)
17         return a.end<b.end;
18     return a.begin<b.begin;
19 } 
20 
21 int main()
22 {    
23     //freopen("F:\课程文件夹\课程之外\ACM文件库\挑战程序设计\数据\test data.txt","r",stdin);
24 
25     //输入
26     int N,T;
27     scanf("%d%d",&N,&T);
28     COW cows[maxn];
29     for(int i=1;i<=N;i++)
30         scanf("%d %d",&cows[i].begin,&cows[i].end);
31      
32     //排序 
33     sort(cows+1, cows+N+1, cmp);
34     
35     //SOLVE
36     int S=0,temp=1,max=0,ans=0;
37     while(S<T)
38     {
39         
40         for( ; cows[temp].begin<=S+1 && temp<=N; temp++ )
41         //在起始时间早于已填充时间的cow里寻找最晚结束工作的cow 
42             max=cows[temp].end>max?cows[temp].end:max;
43 
44         if(S==max)
45         //在已填充时间内找不到可接替并在更晚时间工作的牛，之后死循环 
46             break;
47         S=max;        
48         ans++;
49     }
50     
51     if(S<T)
52         ans=0;
53 
54     ans>0? cout<<ans<<endl : cout<<-1<<endl;
55 }
          View Code
        • POJ 1328：Radar Installation（RE）

                 这题思路不是很清楚，写了个小证明：

                 题面可以转化成使用最少的点占据不同的区间，点应该落在几个区间的公共子区间内。因此此题可以看作是在一些区间中按照公共子区间寻找分组数最少的划分。这个划分应该满足以下的特征（必要条件）：

          1. 不含公共子区间的两个区间一定不在同一分组中；
          2. 分组内的区间有共同的公共子区间，点（雷达）可落在其中任意位置；
          3. 有不同的划分方式达到最小分组数
                  按照贪心的思想证明充分性：

          • 1. 首先对区间排序：优先begin值升序，次end值降序；

            2. 调整公共区间begin为二区间begin之大值，end为二区间end之小值；

            3. 当下一区间begin值大于公共区间end值设立新雷达点；☀（2、3两条保证3中区间之后的区间与当前分组无共同的公共子区间，分组发展完全无法继续扩充）

            4. 在“贪心”地 选择 用来扩充分组的区间时，上述做法是正确的：
            • a) 用来扩充分组的区间出现多个选择，不同选择产生不可逆的分组构成；
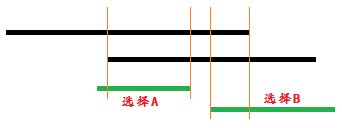
            • b) 备选项之间无公共子区间，按照 必要条件1，二者分属不同分组；
                综上，因为无公共子区间的备选区间各自处于不同分组且各自所在分组都发展完全无法继续扩充，所以按照这个贪心策略得到的划分是正确的。
        • POJ 3190：Stall Reservations（TLE）

                  一开始没有想到优先队列（其实是根本不知道），用了很笨的办法最终TLE，但自信答案没问题

           1 #include <iostream>
 2 #include <cstring>
 3 #include <algorithm>
 4 
 5 using namespace std;
 6 
 7 const int maxn = 50010;
 8 
 9 struct SCHEDUAL
10 {
11     int cowNum, stallNum, begin, end;
12 };
13 
14 bool cmp2(SCHEDUAL a, SCHEDUAL b)
15 {
16     if(a.begin==b.begin)
17         return a.end < b.end;
18     return a.begin < b.begin;
19 }
20 
21 bool cmp3(SCHEDUAL a, SCHEDUAL b)
22 {
23     return a.cowNum < b.cowNum;
24 }
25 
26 int main()
27 {
28     freopen("F:\课程文件夹\课程之外\ACM文件库\挑战程序设计\数据\test data.txt","r",stdin);
29     
30     SCHEDUAL sched[maxn];
31     int N, stallNum[maxn];
32 
33     //输入
34     cin>>N;
35     for(int i=1; i<=N; i++)
36     {
37         cin>>sched[i].begin>>sched[i].end;
38         sched[i].cowNum = i, sched[i].stallNum = -1;
39     }
40     
41     //SOLVE：选择可放入同一stall的cow中最早结束任务的 
42     sort(sched+1, sched+N+1, cmp2);
43     
44     int s=0;    //stallNum数 
45     int L;        //stall end time
46     for(int j=1; j<=N; j++ )
47     //队首循环 
48     {
49         if( sched[j].stallNum == -1 )
50         {
51             s++;
52             sched[j].stallNum = s;
53             L=sched[j].end;
54             for(int k=j+1; k<=N; k++)
55             //队员循环，sort后保证先结束任务的牛在前 
56                 if(sched[k].stallNum == -1 && sched[k].begin > L)
57                 {
58                     sched[k].stallNum = s;     
59                     L = sched[k].end;
60                 }    
61         }
62     }
63     
64     //输出
65     sort(sched+1, sched+1+N, cmp3);
66     
67     cout<<s<<endl;
68     for(int i=1; i<=N; i++)
69         cout<<sched[i].stallNum<<endl;
70 }
          View Code
      • 其他
        • POJ 2393：Yogurt Factory（AC）

                 因为题面说工厂每周生产的商品数量无上限、仓库存储数量无上限，所以这题与其说是贪心不如说是搜索：各周的决策是要么不生产要么生产若干周所需销售的商品数量，每周的cost与之前周的cost加上存储费比较，在最小费用周生产全部商品。直接用O(n^2)的搜索方法过了，交了两次，注意用来存储金额的变量要用long long类型。

           1 #include<iostream>
 2 #include<cstring>
 3 #include<algorithm>
 4 using namespace std;
 5 
 6 const int maxn = 10010;
 7 
 8 struct MANIFEST
 9 {
10     int cost,demand,id,yield;
11 };
12 
13 int main()
14 {
15 freopen("F:\课程文件夹\课程之外\ACM文件库\挑战程序设计\数据\test data.txt","r",stdin);
16     
17     int N,S;
18     MANIFEST manif[maxn],temp;
19     
20     //输入 
21     cin>>N>>S;
22     for(int i=1;i<=N;i++)
23     {
24         manif[i].id = 0;
25         manif[i].yield = -1;
26         cin>>manif[i].cost>>manif[i].demand;
27     }
28         
29     //SOLVE
30     long long ans = 0,tempCost;
31     for(int i=N;i>=1;i--)
32     {
33         manif[0].cost = manif[i].cost;    //manif[0].cost周i最低单价,初始值为当前周cost 
34         for(int j=i-1;j>=1;j--)
35         {
36             tempCost = manif[j].cost + S*(i-j);    //tempCost存储向前搜索过程中的当前最低单价 
37             if(tempCost < manif[0].cost)
38             {
39                 manif[0].cost= tempCost;
40                 manif[i].id = j;
41             }
42         }
43         ans += manif[i].demand * manif[0].cost;
44     }
45     
46     cout<<ans<<endl; 
47 }
          View Code

                 再贴一个别人的更简便的O(N)的方法，这题本来应该就这么做的，我的做题思路还是拖泥带水。

           1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 using namespace std; 
 5 const int maxn=10011;
 6 int n,s;
 7 int y[maxn],c[maxn];
 8 int main()
 9 {
10     freopen("F:\课程文件夹\课程之外\ACM文件库\挑战程序设计\数据\test data.txt","r",stdin);
11     while(scanf("%d%d",&n,&s)!=EOF)
12     {
13         for(int i=0;i<n;i++)
14             scanf("%d%d",&c[i],&y[i]);
15         long long ans=0;
16         for(int i=1;i<n;i++)
17             c[i]=min(c[i-1]+s,c[i]);
18         for(int i=0;i<n;i++)
19             ans+=c[i]*y[i];
20         printf("%lld
",ans);
21     }
22     return 0;
23 }
          View Code
        • POJ 1017：Packets（AC）

          简单题。题面：4/5/6商品必须用新箱子且可与2/1商品共处一箱，3商品可与2/1商品共处一箱，2/1商品可以与其他所有商品共处一箱，球最少需要的箱子数。

          贪心法是使得当前已经使用的箱子的空间尽可能塞满商品，令不同商品共处一箱，使得剩余面积最小（理想情况是只有最后一个箱子有空域面积，其余箱子全部填满）。方法是先考虑可塞入商品中较大者。

          6/5/4商品的individuals都必须使用新箱子，因此先分配之。在本题所给的条件下，箱子空间规则且1商品可以填补单位空间，可以与任何商品共处一箱填补空余，这样只要考虑更大的箱子是否能共处一箱。由于6/5/4/3商品互相不可共处一箱，所以只考虑2商品可否塞入。此题应使用分类讨论的方法来做，虽繁琐但正确。

          考虑如果题目给的箱子大小变为7*7，则4/3商品可共处一箱，那么对于填充4商品确定的新箱子，就要同时考虑3/2两种商品。这里的顺序问题就要考虑先填充哪种商品使得箱子中剩余的面积更小。我认为应该是先3后2。因此此题与题面数据关系很大，数据不同解题方法不同。但是这题其实很简单，如果想快速切题的话只需要具体思考就会很快解决，不需要套用贪心思想完整解释。

          ☀注意即使是这样的简单题也有比较严密的解题逻辑，现在水平太菜不要想着切切切。 
           1 #include<iostream>
 2 #include<cstring>
 3 #include<cmath>
 4 #include<algorithm>
 5 
 6 using namespace std;
 7 
 8 int main()
 9 {
10     //freopen("F:\课程文件夹\课程之外\ACM文件库\挑战程序设计\数据\test data.txt","r",stdin);
11     
12     int num[7], ans, y, x;
13     bool flag;
14     while(1)
15     {
16         //输入 
17         flag = false;
18         for(int i=1;i<=6;i++)
19         {
20             cin>>num[i];
21             if(num[i]>0)
22                 flag = true;
23         }
24                 
25         if(!flag)
26             break;
27         
28         //SOLVE
29         ans = (num[6] + num[5] + num[4] + (num[3]+3)/4);
30 
31         y = num[4]*5;
32         if(num[3]%4 == 1)
33             y += 5;
34         if(num[3]%4 == 2)
35             y += 3;
36         if(num[3]%4 == 3)
37             y += 1;
38         
39         if(num[2]>y)
40             ans += (num[2]-y+8)/9;
41         
42         x = 36*(ans-num[6]) - 25*num[5] - 16*num[4] - 9*num[3] - 4*num[2];
43         if(num[1]>x)
44             ans += (num[1]-x+35)/36;    
45         
46         cout<<ans<<endl;
47     }
48 }
          View Code
        • POJ 3040：Allowance
        • POJ 1862：Stripies（AC）
          一开始蒙对了，后来看了解答才明白，贪心策略是尽量使得大数开方次数更多，因此碰撞顺序是由大到小依次碰撞，有点像哈夫曼树。 
           1 #include<iostream>
 2 #include<cstring>
 3 #include<cmath>
 4 #include<algorithm>
 5 #include<iomanip>  
 6 
 7 using namespace std;
 8 
 9 const int maxn = 105;
10 
11 bool cmp(int a, int b)
12 {
13     return a>b;
14 }
15 
16 int main()
17 {
18     //freopen("F:\课程文件夹\课程之外\ACM文件库\挑战程序设计\数据\test data.txt","r",stdin);
19     
20     int nums[maxn],N;
21     float  ans;
22     cin>>N;
23     for(int i=1; i<=N; i++)
24         cin>>nums[i];
25     
26     sort(nums+1, nums+1+N, cmp);
27     
28     ans = nums[1];
29     for(int i=2; i<=N; i++)
30     {
31         ans = 2*sqrt(ans*(float)nums[i]);
32     }
33     
34     cout <<setiosflags(ios::fixed);
35     cout<<setprecision(3)<<ans<<endl;
36 }
          View Code
        • POJ 3262：Protecting the Flowers
  • 相关阅读:
    sqlite
    c++primer
    c++ std find_last_of
    c语言
    boost serialization
    ssh autologin
    c/c++文件相关
    AndroidTreeView等例子
    and
    解决Gradle 依赖下载慢以及android开发释放c盘空间及android虚拟机访问网络--以及访问本机
  • 原文地址：https://www.cnblogs.com/qin-STU/p/7099341.html
Copyright © 2020-2023  润新知