乘法逆元

先来看看（a/b)%c 这个问题                    不妨引入一个新的概念来让其等于1/b 

切入正题：    

若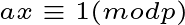  ，gcd（a,b)=1

则称x为a模p的乘法逆元  记x为inv(a)或者a^-1       （a p互质）

---

 (概念性的东西讲完了，那么他有什么存在的意义呢？）

先看看下面这个符号

“≡ ”   简单说明一下 ....a≡ b(mod c)等价于a(mod c)=b(mod c)

 

例如：4关于1模7的乘法逆元为多少？

4X≡1 mod 7

这个方程等价于求一个X和K，满足

4X=7K+1

其中X和K都是整数。

若ax≡1 mod f, 则称a关于1模f的乘法逆元为x。也可表示为ax≡1(mod f)。

当a与f互素时，a关于模f的乘法逆元有解。如果不互素，则无解。如果f为素数，则从1到f-1的任意数都与f互素，即在1到f-1之间都恰好有一个关于模f的乘法逆元。

说了这么多意义何在

(a/b)%p=(a%p/b%p)%p 当然这是错的 例如（30 / 2）%10=5  !=  (30%10 / 2%10)%10=0

所以逆元就是用来解决这种情况  (a/b)%p    解决了a/b所带来的精度问题

 

---

可惜我就会三种解法（废话不多说）

---

 费马小定理+快速幂

费马小定理（a^p-1≡1mod p)     so p为素数  且a p互质

x=a^p-2 mod p   （mod p是因为x是最简的那个值）就可以用到快速幂求解

int  ans=1;
while (b)
{
    if (b&1)///b为奇数
        ans=(ans*a)%p;
     a=(a*a)%p;///b为偶数
     b>>=1;
}
return ans;

直接令b=p-2 求解就行(不会快速幂可以去写luogu p1226）

---

扩展欧几里得 （exgcd）

 （已知整数a，b，扩展欧几里得定理能够在求得gcd（a，b）的同时求得贝祖方程ax+by=gcd（a，b）

中x y的整数解（其中有有一个值可能为负数））

裴蜀定理内容

ax+by=c,x∈Z∗,y∈Z∗成立的充要条件是gcd(a,b)∣c。Z表示正整数集

即c%gcd(a,b)=0   显然贝祖方程有解 

ax≡1mod p  等价于   ax+bp=1  x要有解 则a，p互质  gcd（a，p）=1

 a mod p=a- [a/p]*p;（减去p的倍数）

ax1+by1=ay2+b[x2-[a/b]y2]

证明：

a*x1 + b*y1 = gcd(a,b)

b*x2+(a%b)*y2 = gcd(b,a%b)

由欧几里得算法 gcd(a,b)=gcd(b,a%b)

a*x1 + b*y1 = b*x2+(a- [a/b]*b)*y2

化简得证

b=0时x=1，y=0

gcd（a，0）=a

上代码

int  _exgcd(int a,int b,int &x,int &y)///x代表解
{ 
   if (!b)
   {
     x=1;
     y=0;
     return a ;
   }
   int gcd=_exgcd(b,a%b,x,y);
   int tmp=x;
   x=y;
   y=tmp-(a/b)*y;
   return gcd;//返回最大公约数
}

void _exgcd(int a,int b,int &x,int &y)
{ 
   if (!b)
   {
     x=1;
     y=0;
     return ;
   }
   _exgcd(b,a%b,x,y);///x在调用之前值已经修改
   int tmp=x;
   x=y;
   y=tmp-(a/b)*y;
}

---

线性逆元递推求法

p=ka+q -> k=[p/a]->ka+q ≡ 0mod p

两边同时乘以a和q的逆元k*q^-1+a^-1≡ 0mod p

a^-1≡ -k*q^-1(mod p)  

a^-1≡ -[p/a]*q^-1(mod p)  

a^-1≡ -(p/a)*(p%a)^-1(mod p)

inv[i]=(p-(p/i))*inv[p%i]%p 

#include <bits/stdc++.h>
#define int  long long
using namespace std;
int inv[3000010];
signed  main()
{ 
  int  n,p;
  scanf("%lld%lld",&n,&p);
  inv[1]=1;
  printf("1
");
  for (int i=2;i<=n;++i)
  {
     inv[i]=(p-p/i)*inv[p%i]%p;
     printf("%lld
",inv[i]);
  }
    return 0;
}

权当笔记

（差距一步步扩大，而我还在原地徘徊） 

如有不足，评论区指正

 

 

 

 

 

 

///x在调用之前值已经修改