在半径为 1 的圆上有 n 个点,它们也是圆的 n 等分点,将每个相邻的 n 等分点相连,组成了一个正 n边形,现在你可以在圆上再增加一个点,使得新的 n + 1 边形的面积最大,请输出最大面积。
Input
输入有多组(不超过 100 组)。
每组数据一行一个整数 n 代表点的数量。
3 ≤ n ≤ 100
Output
每组数据输出一行一个数表示加上一个点后的最大面积,结果保留6位小数。
Sample Input
3
Sample Output
1.732051
思路:
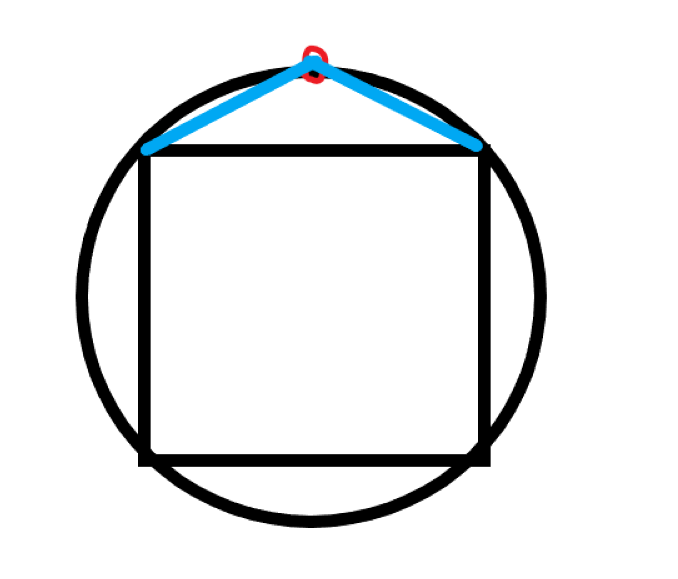
例如n=4的时候,可以证明出第n+1个点选在红点的位置可以使多边形的面积最大。
这个多边形的面积就用余弦定理和三角形内角的关系来求即可。
细节见代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '�', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {ll ans = 1; while (b) {if (b % 2)ans = ans * a % MOD; a = a * a % MOD; b /= 2;} return ans;}
inline void getInt(int* p);
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
typedef long double ld;
ld n;
const ld pi = acos(-1);
int main()
{
//freopen("D:\common_text\code_stream\in.txt","r",stdin);
//freopen("D:\common_text\code_stream\out.txt","w",stdout);
while(cin >> n)
{
ld a=360.0000/n;
a=a/180*pi;
ld S=0.5*sin(a);
S*=(n-1);
a/=2.000;
S+=sin(a);
cout<<fixed<<setprecision(6)<<S<<endl;
}
return 0;
}
inline void getInt(int* p) {
char ch;
do {
ch = getchar();
} while (ch == ' ' || ch == '
');
if (ch == '-') {
*p = -(getchar() - '0');
while ((ch = getchar()) >= '0' && ch <= '9') {
*p = *p * 10 - ch + '0';
}
}
else {
*p = ch - '0';
while ((ch = getchar()) >= '0' && ch <= '9') {
*p = *p * 10 + ch - '0';
}
}
}