Problem Statement
We have a grid with H rows and W columns. At first, all cells were painted white.
Snuke painted N of these cells. The i-th ( 1≤i≤N ) cell he painted is the cell at the ai-th row and bi-th column.
Compute the following:
- For each integer j ( 0≤j≤9 ), how many subrectangles of size 3×3 of the grid contains exactly j black cells, after Snuke painted N cells?
Constraints
- 3≤H≤109
- 3≤W≤109
- 0≤N≤min(105,H×W)
- 1≤ai≤H (1≤i≤N)
- 1≤bi≤W (1≤i≤N)
- (ai,bi)≠(aj,bj) (i≠j)
Input
The input is given from Standard Input in the following format:
H W N a1 b1 : aN bN
Output
Print 10 lines. The (j+1)-th ( 0≤j≤9 ) line should contain the number of the subrectangles of size 3×3 of the grid that contains exactly j black cells.
Sample Input 1
4 5 8 1 1 1 4 1 5 2 3 3 1 3 2 3 4 4 4
Sample Output 1
0 0 0 2 4 0 0 0 0 0
There are six subrectangles of size 3×3. Two of them contain three black cells each, and the remaining four contain four black cells each.
Sample Input 2
10 10 20 1 1 1 4 1 9 2 5 3 10 4 2 4 7 5 9 6 4 6 6 6 7 7 1 7 3 7 7 8 1 8 5 8 10 9 2 10 4 10 9
Sample Output 2
4 26 22 10 2 0 0 0 0 0
Sample Input 3
1000000000 1000000000 0
Sample Output 3
999999996000000004 0 0 0 0 0 0 0 0 0
题意:
给定一个高为h,宽为w的矩阵,然后给你n个黑色块的坐标。
让你求出所有大小为3*3的矩阵分别包含了多少个黑色块,
你只需要输出含有0~9个黑色块的个数的矩阵数量分别是多少。
思路:
由于h和w的数量很大,没有办法进行直接标记模拟。、
我们思考如下:每一个黑色的方块只会对9个3*3的矩阵有贡献。
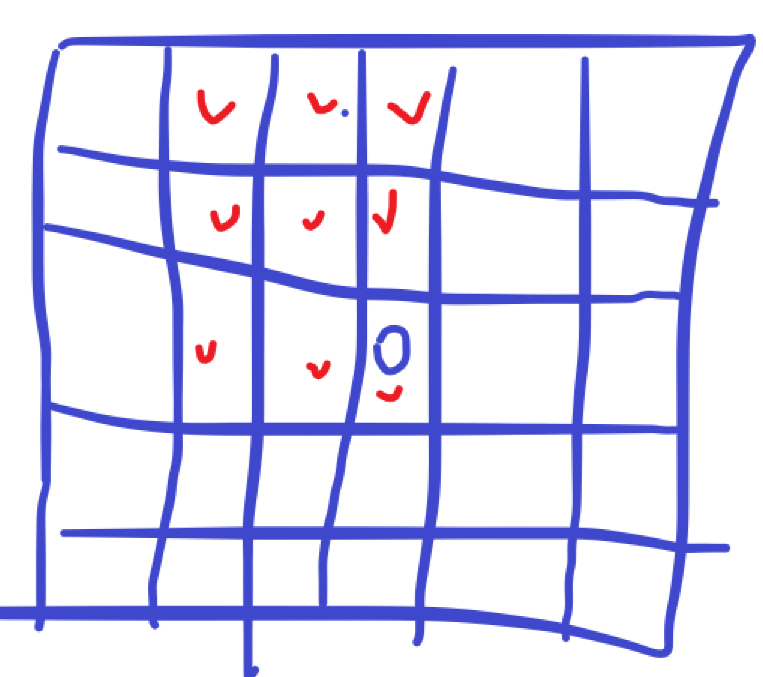
看图:
看图可以知道,蓝色圆圈的位置如果是黑色块,可以对以红色点为左上角起点的3*3的区间有贡献。
那么我们对每一个黑色块算出的一共9个的贡献矩阵,全部加入到一个数组中,排序后处理答案即可。
细节见代码:
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <queue> #include <stack> #include <map> #include <set> #include <vector> #include <iomanip> #define ALL(x) (x).begin(), (x).end() #define rt return #define dll(x) scanf("%I64d",&x) #define xll(x) printf("%I64d ",x) #define sz(a) int(a.size()) #define all(a) a.begin(), a.end() #define rep(i,x,n) for(int i=x;i<n;i++) #define repd(i,x,n) for(int i=x;i<=n;i++) #define pii pair<int,int> #define pll pair<long long ,long long> #define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0) #define MS0(X) memset((X), 0, sizeof((X))) #define MSC0(X) memset((X), '�', sizeof((X))) #define pb push_back #define mp make_pair #define fi first #define se second #define eps 1e-6 #define gg(x) getInt(&x) #define db(x) cout<<"== [ "<<x<<" ] =="<<endl; using namespace std; typedef long long ll; ll gcd(ll a,ll b){return b?gcd(b,a%b):a;} ll lcm(ll a,ll b){return a/gcd(a,b)*b;} ll powmod(ll a,ll b,ll MOD){ll ans=1;while(b){if(b%2)ans=ans*a%MOD;a=a*a%MOD;b/=2;}return ans;} inline void getInt(int* p); const int maxn=1000010; const int inf=0x3f3f3f3f; /*** TEMPLATE CODE * * STARTS HERE ***/ struct node { ll x,y; }a[maxn]; ll n; ll h,w; ll xx[]={-2,-2,-2,-1,-1,-1,0,0,0}; ll yy[]={-2,-1,0,-2,-1,0,-2,-1,0}; ll ans[1000]; ll mod=1e9+7; int main() { //freopen("D:\common_text\code_stream\in.txt","r",stdin); //freopen("D:\common_text\code_stream\out.txt","w",stdout); gbtb; cin>>h>>w>>n; repd(i,1,n) { cin>>a[i].x>>a[i].y; } vector<ll> v; repd(i,1,n) { repd(j,0,8) { ll x=a[i].x+xx[j]; ll y=a[i].y+yy[j]; if(x>=1&&x+2<=h&&y>=1&&y+2<=w) { // cout<<x<<" "<<y<<endl; ll num=(x)*mod+y; v.push_back(num); } } } sort(ALL(v)); v.push_back(-9ll); ll ww=1ll; ll ans0=(h-2ll)*(w-2ll); for(int i=0;i<v.size()-1;i++) { // db(v[i]); if(v[i]==v[i+1]) { ww++; }else { ans[ww]++; ww=1ll; ans0--; } } cout<<ans0<<endl; repd(i,1,9) { cout<<ans[i]<<endl; } return 0; } inline void getInt(int* p) { char ch; do { ch = getchar(); } while (ch == ' ' || ch == ' '); if (ch == '-') { *p = -(getchar() - '0'); while ((ch = getchar()) >= '0' && ch <= '9') { *p = *p * 10 - ch + '0'; } } else { *p = ch - '0'; while ((ch = getchar()) >= '0' && ch <= '9') { *p = *p * 10 + ch - '0'; } } }