一丶冒泡排序:
1.概念:
顾名思义,冒泡排序方式就跟气泡一样,一层一层的往上冒,气泡越大数值越小,当遇到比自己小的气泡,就升到此气泡上面,逐渐比较.
2.算法原理:
冒泡排序算法的运作如下:(从后往前)
>比较相邻的元素。如果第一个比第二个大,就交换他们两个。
>对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
>针对所有的元素重复以上的步骤,除了最后一个。
>持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
代码如下:
#冒泡排序
lst1 = [6,5,4,3,2,1]
def bubble(lst):
#首先获取lst的总长度,为之后的循环比较作准备
length = len(lst)
#一共进行几轮比较,因为下标从零开始,所以一共需要进行length-1轮比较
for i in range(0,length-1):
#一共进行几轮比较,注意range的变化,length-1-i是可以减少跟那些已经排好序的数的比较
for j in range(0,length-1-i):
#比较
if lst[j] > lst[j+1]:
#两数交换位置
lst[j],lst[j+1] = lst[j+1],lst[j]
#打印每次交换后的结果
print(lst)
print("=======================================")
print("bubble sort")
bubble(lst1)
时间复杂度:O(n^2). 需要进行的比较次数为第一轮 n-1,n-2....1, 总的比较次数为 n*(n-1)/2
二丶递归
在函数中调用本身就是递归,递归深度最高可达1000,但到998就会报错
count = 1
def func():
global count
print("我是大帅哥", count)
count = count + 1
func()
func()
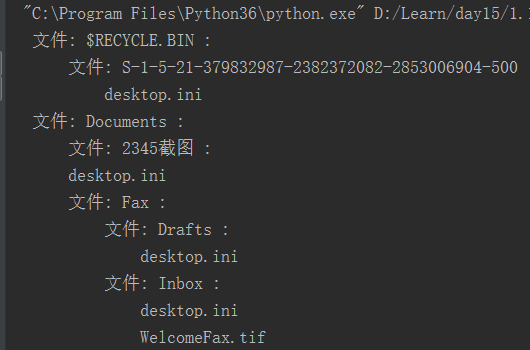
递归应用:我们可以使用递归来遍历各种树形结构,比如我们的文件夹系统,可以使用递归来遍历该文件夹下所有文件
# 遍历 D:文件夹, 打印出所有的文件和普通文件的文件名
import os
def func(filepath, n): # d:/
# 1,打开这个文件夹
files = os.listdir(filepath)
# 2. 拿到每一个文件名
for file in files: # 文件名
# 3. 获取到路径
f_d = os.path.join(filepath, file) # d:/文件名/
# 4. 判断是否是文件夹
if os.path.isdir(f_d):
# 5. 如果是文件夹. 继续再来一遍
print(" "*n,"文件:" ,file,":") # 打印文件名
func(f_d, n + 1)
else: # 不是文件夹. 普通文件
print(" "*n, file)
func("d:/",0)
三丶二分法查找
二分法查找每次都能排除一半的数据,查找效率非常高,但是局限性较大,必须是有序序列才可以使用二分法查找
lst = [22, 33, 44, 55, 66, 77, 88, 99, 101 , 238 , 345 , 456 , 567 , 678 , 789]
def func(n,left,right):
if left <= right: #左右两个边界
mid = (left+right)//2 #中间值
if n > lst[mid]:
left = mid+1
return func(n,left,right) #递归的入口
elif n < lst[mid]:
right = mid-1
return func(n,left,right) #递归
else:
print("找到了")
return "下标为%s"% mid #通过return返回. 终止递归
else:
print("没有这个数") #递归的出口
return -1
print(func(99,0,len(lst)-1))
另附一个最快查找方法:
# 时间复杂度最低, 空间复杂度最低
lst1 = [5, 6, 7, 8]
lst2 = [0, 0, 0, 0, 0, 0, 0, 0, 0]
for el in lst1:
lst2[el] = 1
print(lst2[6])
lst1中最大的数是多少.lst2中就有多少个数,全为0,然后循环lst1,将其中的数在lst2中变为1,查找时如果返回值为1则代表存在这个数,如果为0则不存在,时间复杂度为O(1)

