一、什么是二分查找
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列
二、算法复杂度
二分查找的基本思想是将n个元素分成大致相等的两部分,取a[n/2]与x做比较,如果x=a[n/2],则找到x,算法中止;如果x<a[n/2],则只要在数组a的左半部分继续搜索x,如果x>a[n/2],则只要在数组a的右半部搜索x.
时间复杂度即是while循环的次数。
总共有n个元素,
渐渐跟下去就是n,n/2,n/4,....n/2^k(接下来操作元素的剩余个数),其中k就是循环的次数
由于你n/2^k取整后>=1
即令n/2^k=1
可得k=log2n,(是以2为底,n的对数)
所以时间复杂度可以表示O(h)=O(log2n)
三、如何理解二分查找
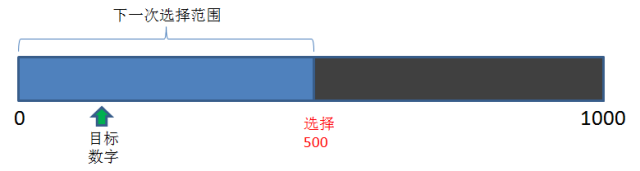
给定范围0到1000的整数:

第一次我们选择500,发现偏大了,
那么下一次的选择范围,就变成了1到499:
第二次我们选择250,发现还是偏大了,
那么下一次的选择范围,就变成了1到249:

第三次我们选择125,发现偏小了,
那么下一次的选择范围,就变成了126到249:

以此类推,最坏的情况需要猜测多少次呢?
答案是 log1000 = 10次,
也就是让原本的区间范围进行10次 “折半”。
四、代码实现
1.非递归方式
1 import java.util.Arrays; 2 3 public class test07 { 4 public static void main(String[] args) { 5 int[] arr = new int[]{15,66,48,9,54,11,87,100,40,8,9,7,12,13}; 6 int key = 11; //要查找的数 7 Arrays.sort(arr); //二分查找,之前一定要对数组进行元素排序 8 System.out.println(Arrays.toString(arr)); //打印数组 9 System.out.println(key+"元素的索引"+binarySearch(arr,key)); 10 } 11 public static int binarySearch(int[] array,int key){ 12 //头指针初始位置 13 int low = 0; 14 //尾指针初始位置 15 int high = array.length - 1; 16 //判断查找的数是否在数组中,如果此处不加判断,则可能报java.lang.StackOverflowError栈内存溢出 17 if(low>high||key>array[high]||key<array[low]){ 18 return -1; 19 } 20 while(low<=high){ 21 //计算中间值的索引,防止溢出 22 int mid = low+ (high - low)/2; 23 if(key==array[mid]){ 24 return mid; //返回查询到的索引位置 25 }else if (key>array[mid]){ 26 low = mid+1; //mid所对应的的值比key小,key应该在右边 27 }else { 28 high = mid-1; //mid所对应的的值比key大,key应该在左边 29 } 30 } 31 //若没有,则返回-1 32 return -1; 33 } 34 }

2.非递归方式
1 import java.lang.annotation.ElementType; 2 import java.util.Arrays; 3 4 public class test07 { 5 public static void main(String[] args) { 6 int[] arr = new int[]{15,66,48,9,54,11,87,100,40,8,9,7,12,13}; 7 int key = 11; //要查找的数 8 //头指针初始位置 9 int low = 0; 10 //尾指针初始位置 11 int high = arr.length - 1; 12 Arrays.sort(arr); //二分查找,之前一定要对数组进行元素排序 13 System.out.println(Arrays.toString(arr)); //打印数组 14 System.out.println(key+"元素的索引"+binarySearch(arr,low,high,key)); 15 } 16 public static int binarySearch(int[] array,int low,int high,int key){ 17 //判断查找的数是否在数组中,如果此处不加判断,则可能报java.lang.StackOverflowError栈内存溢出 18 if(low>high||key>array[high]||key<array[low]){ 19 return -1; 20 } 21 //计算中间值的索引,防止溢出 22 int mid = low+ (high - low)/2; 23 if (key>array[mid]){ 24 return binarySearch(array,mid+1,high,key); //mid所对应的的值比key小,key应该在右边 25 }else if(key<array[mid]){ 26 return binarySearch(array,low,mid-1,key); //mid所对应的的值比key大,key应该在左边 27 }else{ 28 return mid; 29 } 30 } 31 }

二分查找中值(mid)计算 二分查找中值计算有三种方式:
- int mid = (low + high)/ 2;
- int mid = low + (high - low) / 2;
- int mid = (high + low) >>> 1
- 上述两种算法看似第一种要简洁,第二种提取之后,跟第一种没有什么区别。但是实际上上述两种计算是有区别的,
- 第一种的做法是在极端情况下计算的,(low + high)存在着溢出的风险,进而有可能得到错误的mid结果,导致程序错误;
- 而第二种算法能够保证计算出来的mid值一定大于low、小于high,不存在溢出的问题。
- 针对第一种算法为了防止溢出问题,可以使用:int mid = (high + low) >>> 1; 解决此问题。
五、二分查找的优缺点:
优点:比较次数少,查找速度快,平均性能好。
缺点:必须有序,必须是数组。