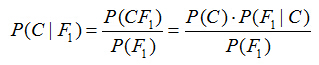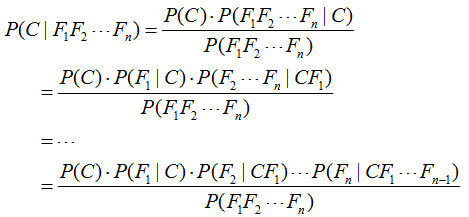朴素贝叶斯分类器是一个以贝叶斯定理为基础,广泛应用于情感分类领域的优美分类器。本文我们尝试使用该分类器来解决上一篇文章中影评态度分类。
1、贝叶斯定理
假设对于某个数据集,随机变量C表示样本为C类的概率,F1表示测试样本某特征出现的概率,套用基本贝叶斯公式,则如下所示:
上式表示对于某个样本,特征F1出现时,该样本被分为C类的条件概率。那么如何用上式来对测试样本分类呢?
举例来说,有个测试样本,其特征F1出现了(F1=1),那么就计算P(C=0|F1=1)和P(C=1|F1=1)的概率值。前者大,则该样本被认为是0类;后者大,则分为1类。
对该公示,有几个概念需要熟知:
先验概率(Prior)。P(C)是C的先验概率,可以从已有的训练集中计算分为C类的样本占所有样本的比重得出。
证据(Evidence)。即上式P(F1),表示对于某测试样本,特征F1出现的概率。同样可以从训练集中F1特征对应样本所占总样本的比例得出。
似然(likelihood)。即上式P(F1|C),表示如果知道一个样本分为C类,那么他的特征为F1的概率是多少。
对于多个特征而言,贝叶斯公式可以扩展如下:
分子中存在一大串似然值。当特征很多的时候,这些似然值的计算是极其痛苦的。现在该怎么办?
2、朴素的概念
为了简化计算,朴素贝叶斯算法做了一假设:“朴素的认为各个特征相互独立”。这么一来,上式的分子就简化成了:
P(C)*P(F1|C)*P(F2|C)...P(Fn|C)。
这样简化过后,计算起来就方便多了。
这个假设是认为各个特征之间是独立的,看上去确实是个很不科学的假设。因为很多情况下,各个特征之间是紧密联系的。然而在朴素贝叶斯的大量应用实践实际表明其工作的相当好。
其次,由于朴素贝叶斯的工作原理是计算P(C=0|F1...Fn)和P(C=1|F1...Fn),并取最大值的那个作为其分类。而二者的分母是一模一样的。因此,我们又可以省略分母计算,从而进一步简化计算过程。
另外,贝叶斯公式推导能够成立有个重要前期,就是各个证据(evidence)不能为0。也即对于任意特征Fx,P(Fx)不能为0。而显示某些特征未出现在测试集中的情况是可以发生的。因此实现上通常要做一些小的处理,例如把所有计数进行+1(加法平滑(additive smoothing,又叫拉普拉斯平滑(Laplace smothing))。而如果通过增加一个大于0的可调参数alpha进行平滑,就叫Lidstone平滑。
例如,在所有6个分为C=1的影评样本中,某个特征F1=1不存在,则P(F1=1|C=1) = 0/6,P(F1=0|C=1) = 6/6。
经过加法平滑后,P(F1=1|C=1) = (0+1)/(6+2)=1/8,P(F1=0|C=1) = (6+1)/(6+2)=7/8。
注意分母的+2,这种特殊处理使得2个互斥事件的概率和恒为1。
最后,我们知道,当特征很多的时候,大量小数值的小数乘法会有溢出风险。因此,通常的实现都是将其转换为log:
log[P(C)*P(F1|C)*P(F2|C)...P(Fn|C)] = log[P(C)]+log[P(F1|C)] + ... +log[P(Fn|C)]
将乘法转换为加法,就彻底避免了乘法溢出风险。
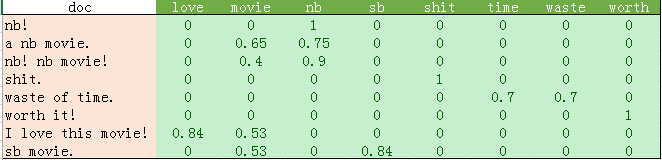
为确保掌握朴素贝叶斯分类原理,我们先使用上一篇文章最后的文本向量化结果做一个例子:
上述训练集中共8个样本,其中C=0的3个,C=1的5个。现在,假设给你一个测试样本"nb movie",使用加一平滑进行朴素贝叶斯的分类过程如下:
P(C=0)=3/8, P(C=1)=5/8。特征F1="nb", F2="movie"。
分为C=0的概率:P(F1=1, F2=1|C=0) = P(C=0)*P(F1=1|C=0)*P(F2=1|C=0) = 3/8 * (0+1)/(3+2) * (1+1)/(3+2) = 3/8 * 1/5 * 2/5 = 0.03。
分为C=1的概率:P(F1=1, F2=1|C=1) = P(C=1)*P(F1=1|C=1)*P(F2=1|C=1) = 5/8 * (3+1)/(5+2) * (3+1)/(5+2) = 5/8 * 4/7 * 4/7 = 0.20。
分为C=1的概率更大。因此将该样本分为C=1类。
(注意:实际计算中还要考虑上表中各个值的TF-IDF,具体计算方式取决于使用哪一类贝叶斯分类器。分类器种类见本文最后说明)
3、测试数据
本文使用上一篇博客中提到的康奈尔大学网站的2M影评数据集。下载地址http://download.csdn.net/detail/lsldd/9346233
每一个特征值就是一个单词的TF-IDF。当然,也可以简单的使用单词出现的次数。
使用这个比较大的数据集,可以做一点点数据预处理的优化来避免每次都去硬盘读取文件。第一次运行时,把读入的数据保存起来,以后就不用每次再去读取了。
#保存 movie_reviews = load_files('endata') sp.save('movie_data.npy', movie_data) sp.save('movie_target.npy', movie_target) #读取 movie_data = sp.load('movie_data.npy') movie_target = sp.load('movie_target.npy')
4、代码与分析
Python代码如下:
# -*- coding: utf-8 -*- from matplotlib import pyplot import scipy as sp import numpy as np from sklearn.datasets import load_files from sklearn.cross_validation import train_test_split from sklearn.feature_extraction.text import CountVectorizer from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.naive_bayes import MultinomialNB from sklearn.metrics import precision_recall_curve from sklearn.metrics import classification_report ''' movie_reviews = load_files('data') #保存 sp.save('movie_data.npy', movie_reviews.data) sp.save('movie_target.npy', movie_reviews.target) ''' #读取 movie_data = sp.load('movie_data.npy') movie_target = sp.load('movie_target.npy') x = movie_data y = movie_target #BOOL型特征下的向量空间模型,注意,测试样本调用的是transform接口 count_vec = TfidfVectorizer(binary = False, decode_error = 'ignore', stop_words = 'english') #加载数据集,切分数据集80%训练,20%测试 x_train, x_test, y_train, y_test = train_test_split(movie_data, movie_target, test_size = 0.2) x_train = count_vec.fit_transform(x_train) x_test = count_vec.transform(x_test) #调用MultinomialNB分类器 clf = MultinomialNB().fit(x_train, y_train) doc_class_predicted = clf.predict(x_test) #print(doc_class_predicted) #print(y) print(np.mean(doc_class_predicted == y_test)) #准确率与召回率 precision, recall, thresholds = precision_recall_curve(y_test, clf.predict(x_test)) answer = clf.predict_proba(x_test)[:,1] report = answer > 0.5 print(classification_report(y_test, report, target_names = ['neg', 'pos']))
输出结果如下所示:
0.821428571429
precision recall f1-score support
neg 0.78 0.87 0.83 135
pos 0.87 0.77 0.82 145
avg / total 0.83 0.82 0.82 280
如果进行多次交叉检验,可以发现朴素贝叶斯分类器在这个数据集上能够达到80%以上的准确率。如果你亲自测试一下,会发现KNN分类器在该数据集上只能达到60%的准确率,相信你对朴素贝叶斯分类器应该能够刮目相看了。而且要知道,情感分类这种带有主观色彩的分类准则,连人类都无法达到100%准确。
要注意的是,我们选用的朴素贝叶斯分类器类别:MultinomialNB,这个分类器以出现次数作为特征值,我们使用的TF-IDF也能符合这类分布。
其他的朴素贝叶斯分类器如GaussianNB适用于高斯分布(正态分布)的特征,而BernoulliNB适用于伯努利分布(二值分布)的特征。
附:
使用python训练贝叶斯模型预测贷款逾期
准备工作
首先是开始前的准备工作,导入所需的库文件。依次为数值计算库numpy,科学计算库pandas,交叉验证库cross_validation和朴素贝叶斯算法库GaussianNB。
#导入数值计算库 import numpy as np #导入科学计算库 import pandas as pd #导入交叉验证库 from sklearn import cross_validation #导入GaussianNB库 from sklearn.naive_bayes import GaussianNB
读取并查看数据表
读取并创建名为loan_status的贷款历史数据。这里我们只包含了两个特征和极少的数据用于说明计算的过程。在真实的环节中要预测贷款的逾期情况所需数据量要大得多。按宜人贷公布的信息,他们的风控系统包含了250个特征和超过100万条的历史贷款数据,并且还有一个黑名单系统。
#读取历史贷款状态数据并创建loan_status数据表 loan_status=pd.DataFrame(pd.read_excel('loan_status.xlsx'))
以下是贷款数据表中具体的内容,两个特征分布为借款人的年龄,借款天数。结果显示了这笔贷款最终的状态。
#查看数据表内容 loan_status.head()
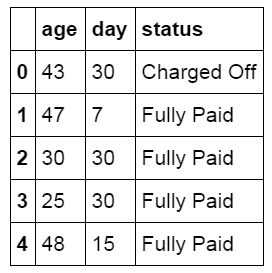
使用columns获得数据表的列名称。
#查看数据表列标题 loan_status.columns Index(['age', 'day', 'status'], dtype='object')
设置模型特征X及目标Y
将借款人的年龄和借款天数设置为特征X,将贷款的最终还款状态设置为目标Y。
#设置特征X X=np.array(loan_status[['age','day']]) #设置目标Y Y=np.array(loan_status['status'])
分布查看特征和目标数据的维度。
#查看数据集的维度 X.shape,Y.shape ((823, 2), (823,))
将数据分割为训练集和测试集
使用交叉检验库通过随机方式将特征数据和目标数据分为测试集和训练集,其中训练集为原数据集的60%,测试集为40%。
#将数据集拆分为训练集和测试集 X_train,X_test,y_train,y_test=cross_validation.train_test_split(X,Y,test_size=0.4,random_state=0)
再次查看训练集和测试集数据的维度。
#查看训练集维度 X_train.shape,y_train.shape ((493, 2), (493,)) #查看测试集维度 X_test.shape,y_test.shape ((330, 2), (330,))
建立高斯朴素贝叶斯模型。
#建立模型 clf=GaussianNB()
使用训练集数据对模型进行训练。
#使用训练集对模型进行训练 clf.fit(X_train,y_train) GaussianNB(priors=None)
使用测试集数据对训练后的模型进行测试,模型预测的准确率为69%。
#使用测试集数据检验模型准确率 clf.score(X_test,y_test) 0.68787878787878787
使用模型进行分类预测
使用训练后的高斯朴素贝叶斯模型对新贷款用户的数据进行分类预测。首先查看分类的结果。与之前的目标Y一样,结果为Charged Off和Fully Paid。
clf.classes_array([‘Charged Off’, ‘Fully Paid’], dtype='<U11′)
输入一组贷款用户特征,年龄为25岁,借款天数30天。模型预测这笔贷款的结果为Fully Paid。
clf.predict([[25,30]])