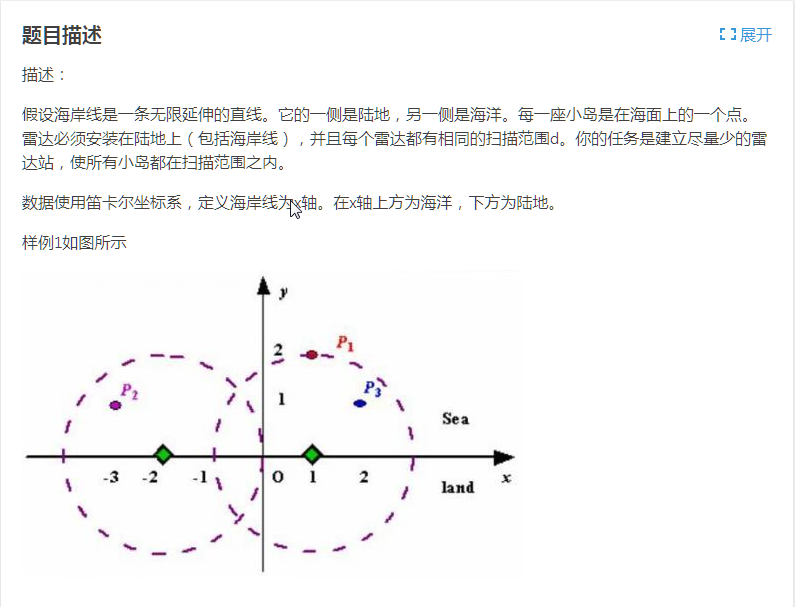
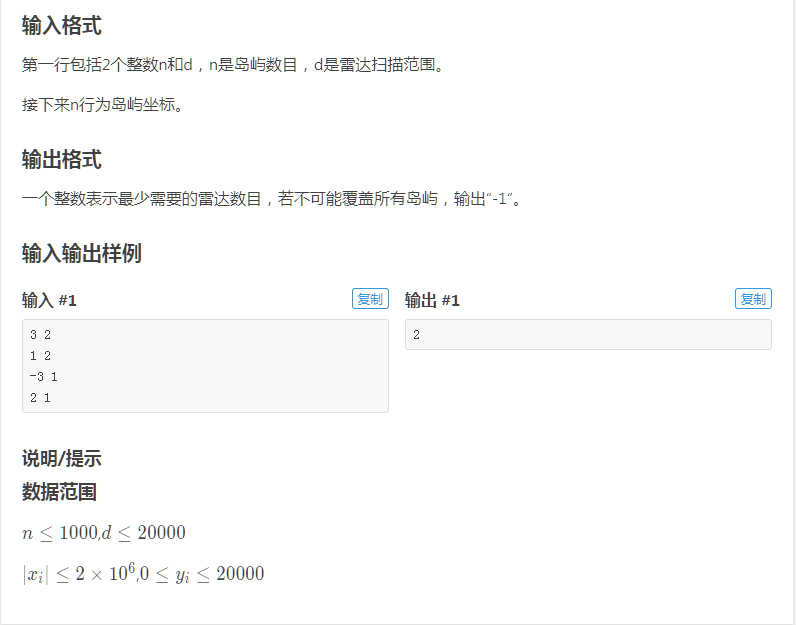
这道题我们看上去没有思路。但是当我们知道了岛屿的位置和雷达的扫描半径后,我们就可以求出要扫描到每个岛屿,雷达的安装范围。同时,根据贪心原理,很明显要把雷达尽量布置在海岸线上。这样,我们就将本题转化为了一道区间选点问题,只需要选择尽量少的点,满足每一个扫描区间内都有一个点即可。
下面分析代码。
首先,我们还是要先定义好岛屿个数n和雷达的扫描半径d,并设置一个cnt来记录最少的雷达数。
同时,我们来定义一个结构体来记录每一个岛屿所对应的雷达扫描区间。设置两个double变量l和r来标记边界。得到代码如下:
1 #include<iostream>
2 using namespace std;
3 int n,d,ans;
4 struct qujian{
5 double l,r;
6 }t[1005];
7 int main(){
8 return 0;
9 }
接下来,我们要进行读入。先读入岛屿树木n和雷达扫描半径d,然后从1到n依次读入每个岛屿的坐标。因为读入的并不是区间的左边界和右边界,所以我定义了两个整型变量a,b表示坐标(因为将该坐标转化为区间后,该坐标不再有作用,所以可以直接覆盖)。如果b>d,说明无论如何雷达也扫描不到该岛屿,则需要输出-1,并且直接return 0。否则,我们可以根据两点间距离公式得出区间的左边界l=a-sqrt(d*d-b*b);右边界r=a+sqrt(d*d-b*b)。得到代码如下:
1 #include<iostream>
2 using namespace std;
3 int n,d,ans,a,b;
4 double position;
5 struct qujian{
6 double l,r;
7 }t[1005];
8 int main(){
9 cin>>n>>d;
10 for(i=1;i<=n;i++){
11 cin>>a>>b;
12 if(b>d){
13 cout<<-1<<endl;
14 return 0;
15 }
16 t[i].l=a-sqrt(d*d-b*b);
17 t[i].r=a+sqrt(d*d-b*b);
18 }
19 return 0;
20 }
接下来,我们便可以使用区间选点问题的处理方法进行计算。
首先,我们仍需要按照区间的右边界进行排序。这里仍然使用<algorithm>中的排序函数sort,并且需要手写cmp函数。注意函数的类型名为double。然后,我们需要将ans记录的雷达数初始化。
下一步,我们要枚举每一个区间。注意这里和一般的区间选点问题不同的是,区间的边界和雷达的安装都是double类型的,而且每个区间固定只需要安装一个点。所以我们只需要定义一个double类型的变量position,来记录当前的最靠右的雷达位置。
这里需要注意的是,在枚举每个岛屿时,第一个岛屿并不是从0点开始的,所以在初始化时,我们需要将r初始化为第一个节点的右边界,而非0,同时将ans初始化为1(默认第一个雷达安装在第一个岛屿右边界),并从2开始枚举安装雷达。
下面是本题的完整代码:
1 #include<iostream>
2 #include<algorithm>
3 #include<cmath>
4 using namespace std;
5 int n,d,ans,a,b,i;
6 double position;
7 struct qujian{
8 double l,r;
9 }t[1005];
10 double cmp(qujian a,qujian b){
11 return a.r<b.r;
12 }
13 int main(){
14 cin>>n>>d;
15 for(i=1;i<=n;i++){
16 cin>>a>>b;
17 if(b>d){
18 cout<<-1<<endl;
19 return 0;
20 }
21 t[i].l=a-sqrt(d*d-b*b);
22 t[i].r=a+sqrt(d*d-b*b);
23 }
24 sort(t+1,t+n+1,cmp);
25 ans=1;
26 position=t[1].r;
27 for(i=2;i<=n;i++){
28 if(position>=t[i].l){
29 continue;
30 }else{
31 ans++;
32 position=t[i].r;
33 }
34 }
35 cout<<ans<<endl;
36 return 0;
37 }