题面:
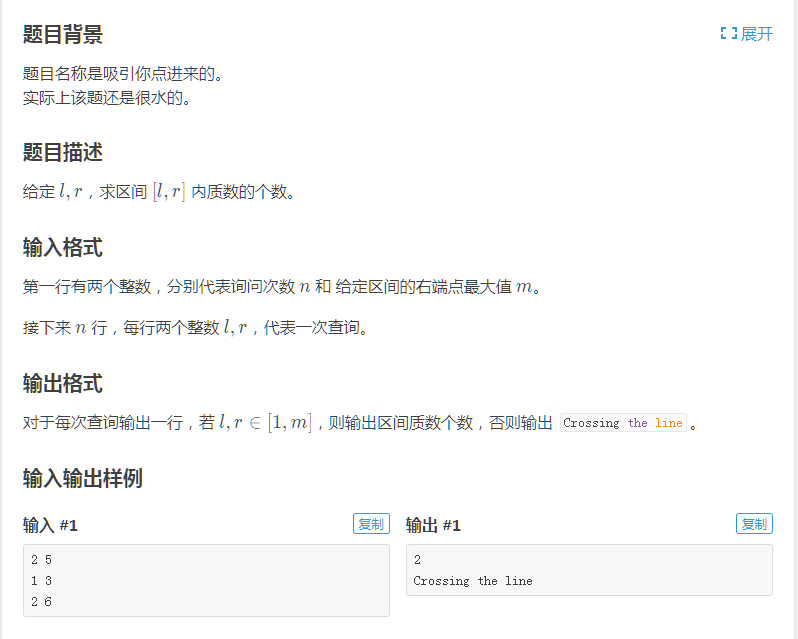
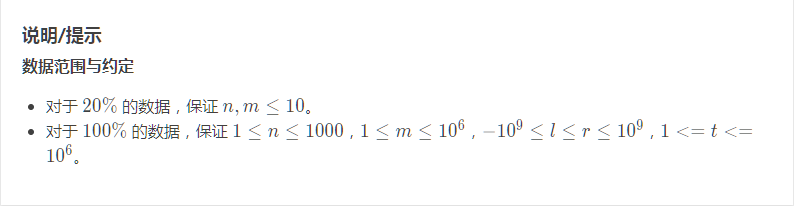
这道题很明显是一道数论的题目,涉及的内容主要为素数的问题。首先看数据范围,其实这道题的数据范围是很水的。因此在这里主要介绍2种方法。
法一,首先题目给出了给定区间右端点的最大值,因此我们对于每一个输入的l和r,要先进行判断其是否合法,只有合法的区间才能进一步处理。而合法的标准是右端点r<=m且左端点l>=1(注意这里要小心,不要想当然,题目中出了四个点来卡它)。
因此我们可以对于每一个给定的合法区间l到r,枚举l到r中的所有元素,依次判断该元素是否为素数。如果为素数,则cnt++。这里对于素数的判断我使用了O(√n)的试除法。很明显该方法时间复杂度过大。
代码(含注释):
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 int n,m,i,l,r,h,cnt; 5 inline bool prime(int n){//判断每一个数是否为素数 6 if(n<2){//<2的数一定不是素数,要小心 7 return false; 8 }else{ 9 int j; 10 for(j=2;j*j<=n;j++){//进行枚举 11 if(n%j==0){//如果n有2~√n的质因子,则n一定非质 12 return false; 13 } 14 } 15 } 16 return true; 17 } 18 int main(){ 19 scanf("%d %d",&n,&m); 20 for(i=1;i<=n;i++){ 21 scanf("%d %d",&l,&r); 22 if(r>m||l<1){//判断区间是否合法 23 printf("Crossing the line "); 24 }else{ 25 cnt=0;//统计每个区间内的素数个数 26 for(h=l;h<=r;h++){ 27 if(prime(h)==true){ 28 cnt++; 29 } 30 } 31 printf("%d ",cnt); 32 } 33 } 34 return 0; 35 }
分数:81分(完全没有想到!)
法二,既然法一出现了超时,那我们就要想方法进行优化。在法一中,TLE的主要原因便是对于同一个素数需要进行多次判断。而如果能够在一定的预处理基础上将O(√n)变成O(1),那么时间就加快了。
题目明显预先给出了r的最大值,目的即是启发我们进行预处理。因此我们可以在O(n)的时间复杂度内预先找出1~m中的质数(我使用了线性筛),然后进行寻找和统计。
代码(含注释):
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 int n,m,i,j,l,r,h,cnt,num; 5 int prime[100000005],v[100000005]; 6 int main(){ 7 scanf("%d %d",&n,&m); 8 num=0;//质数数量 9 for(i=2;i<=m;i++){ 10 if(v[i]==0){//i是质数 11 v[i]=i;//质数的最小质因子是他自己 12 prime[++num]=i;//记录质数 13 } 14 for(j=1;j<=num;j++){//给当前的数i乘上一个质因子 15 if(prime[j]>v[i]||prime[j]>m/i){ 16 break;//i有比prime[j]更小的质因子,或者超出n的范围 17 } 18 v[i*prime[j]]=prime[j]; 19 } 20 } 21 for(i=1;i<=n;i++){ 22 scanf("%d %d",&l,&r); 23 if(r>m||l<1){ 24 printf("Crossing the line "); 25 }else{ 26 cnt=0; 27 for(h=1;h<=m;h++){ 28 if(prime[h]>=l&&prime[h]<=r){ 29 cnt++; 30 } 31 } 32 printf("%d ",cnt); 33 } 34 } 35 return 0; 36 }
即可获得AC。