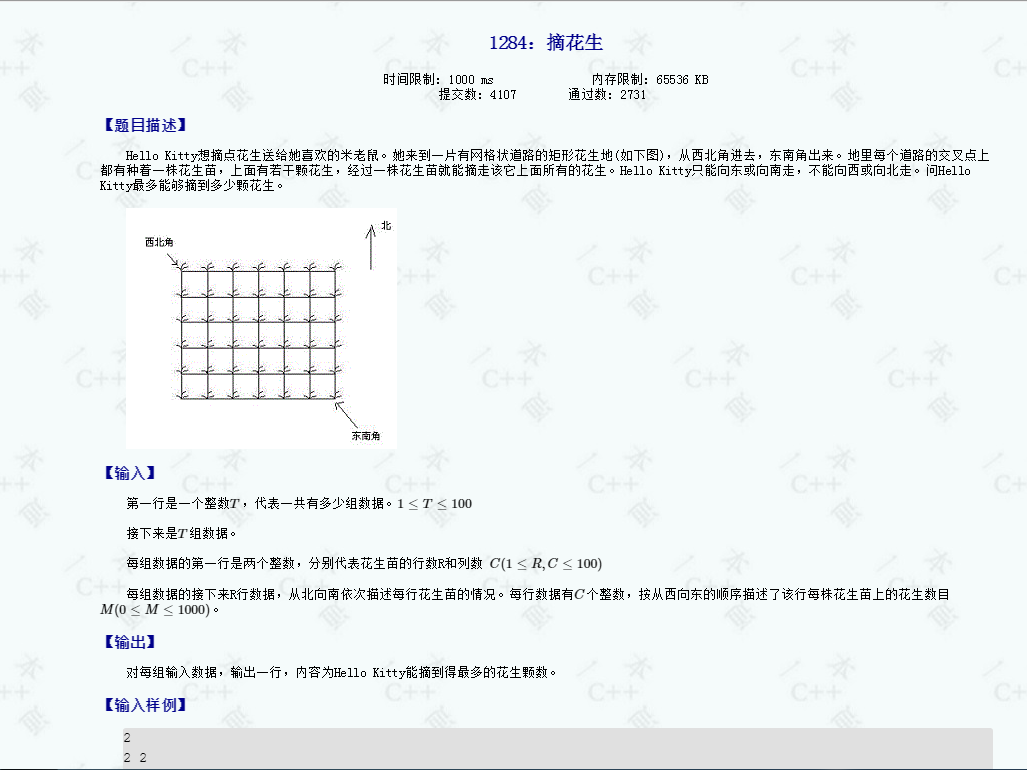
首先,这是一道DP的题嗯嗯 ……
既然这道题一个测试点有多张地图,所以我就定义了一个三维数组map来存储每一张矩阵图。
与此同时,再开一个数组dp[105][105][105]来表示每张图上从左上角的起始点到每个点能摘到的最多的花生。
再然后,开一个c[105]数组,一个r[105]数组来存储每张图的边界。
最后再开一个指针i表示当前在研究第几个矩阵、指针j表示该个正在被研究的数组的行,指针h表示该个正在被研究的数组的列。
这样,main函数以前的定义部分就写好了。
#include<iostream>
#include<algorithm>
using namespace std;
int map[105][105][105];
int dp[105][105][105];
int T,i,j,h;
int c[105],r[105];
main函数内,先输入矩阵的数量,然后开始第一个for循环枚举研究第一个矩阵。
#include<iostream>
#include<algorithm>
using namespace std;
int map[105][105][105];
int dp[105][105][105];
int T,i,j,h;
int c[105],r[105];
int main(){
cin>>T;
for(i=1;i<=T;i++){
}
}
在大循环内,首先我们要读入每一张矩阵的长和宽c[i]和r[i],然后读入这张地图。
接下来,要对dp数组进行初始化。
先初始化dp[i][1][1]为map[1][1][1],因为这个位置没有其它位置可以到达。
然后初始化第一行和第一列,其中第一行只能从左边过来,第一列只能从上边到来,所以
dp[i][j][1]=dp[i][j-1][1]+map[i][j][1];//初始化行
dp[i][1][h]=dp[i][1][h-1]+map[i][1][h];//初始化列
这样我们就得到了进一步完善的代码:
#include<iostream>
#include<algorithm>
using namespace std;
int map[105][105][105];
int dp[105][105][105];
int T,i,j,h;
int c[105],r[105];
int main(){
cin>>T;
for(i=1;i<=T;i++){
cin>>c[i]>>r[i];
for(j=1;j<=c[i];j++){//j和h代表每一张map的行和列
for(h=1;h<=r[i];h++){
cin>>map[i][j][h];
}
}
dp[i][j][h]=map[i][1][1];
for(j=1;j<=c[i];j++){//初始化行
dp[i][j][1]=dp[i][j-1][1]+map[i][j][1];
}
for(h=1;h<=r[i];h++){
dp[i][1][h]=dp[i][1][h-1]+map[i][1][h];
}
}
}
最后就是最重要的DP部分!
首先,第一行和第一列已经初始化完成,所以要从第二行、第二列开始枚举。
然后,我们要考虑让该点的dp值更大(摘更多的花生)应该从左边来还是从上面来(因为题目中说只能往下走或往右走)。这里需要使用一个max函数,我用了STL中的头文件<algorithm>。
我们算出了从那边过来该点的dp值更大,再加上在这个点能摘的花生数,就可以得出该点最多能摘几个花生。
这样就得出了状态转移方程。
dp[i][j][h]=max(dp[i][j-1][h],dp[i][j][h-1])+map[i][j][h];
这样,我们就又一次完善了我们的代码。(前面记得要加头文件)
最后还需要输出!
这很简单,只需要输出每个矩阵最右下角的位置的数值即可(因为其它位置都还能再移动去摘花生)
这样,我们就得到了完整的代码。
1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 int map[105][105][105]; 5 int dp[105][105][105]; 6 int T,i,j,h; 7 int c[105],r[105]; 8 int main(){ 9 cin>>T; 10 for(i=1;i<=T;i++){ 11 cin>>c[i]>>r[i]; 12 for(j=1;j<=c[i];j++){//j和h代表每一张map的行和列 13 for(h=1;h<=r[i];h++){ 14 cin>>map[i][j][h]; 15 } 16 } 17 dp[i][j][h]=map[i][1][1]; 18 for(j=1;j<=c[i];j++){//初始化行 19 dp[i][j][1]=dp[i][j-1][1]+map[i][j][1]; 20 } 21 for(h=1;h<=r[i];h++){ 22 dp[i][1][h]=dp[i][1][h-1]+map[i][1][h]; 23 } 24 for(j=2;j<=c[i];j++){ 25 for(h=2;h<=r[i];h++){ 26 dp[i][j][h]=max(dp[i][j-1][h],dp[i][j][h-1])+map[i][j][h]; 27 } 28 } 29 cout<<dp[i][c[i]][r[i]]<<endl; 30 } 31 return 0; 32 }
这就是关于本题的具体讲解(第一次发DP题的题解,害怕……)