二叉树的定义: 二叉树是一种树形结构: 特点是与每个节点关联的子节点至多有两个(可为0,1,2) 每个节点的子节点有关联位置关系 定义: 二叉树是节点的有限集合,该集合或为空集,或由一个根元素和两棵不相交的二叉树组成(递归定义) 二叉树的两棵子树分别称为它的左子树和右子树 二叉树的5种基本形态: 空二叉树 只有根节点 只有左子树,右子树为空 只有右子树,左子树为空 左右子树都不为空 满的和完全的二叉树: 满二叉树:树中每个分支节点(非叶节点)都有两棵非空子树 完全二叉树:除最下两层外,其余节点度数都是2,如果最下面的节点不满,则所有空位都在右边,左边没有空位,如下图 扩充二叉树(由已有非空二叉树生成的一种二叉树): 是原二叉树的最小节点扩充,使原树中所有节点的度数都变成2 二叉树的性质: 性质1. 非空二叉树第 i 层上至多有 2i 个结点(i ≥ 0) 性质2. 高度为 k 的二叉树至多有 2k-1 个结点(k ≥ 0) 性质3. 对任何非空二叉树 T,若其叶结点个数为 n0,度数为 2 的结点 个数为 n2,则n0 = n2 + 1 性质4. n 个结点的完全二叉树的高度 k = ⎡log2(n+1)⎤ 性质5. 满二叉树里的叶结点比分支结点多一个 二叉树的数据结构 基本操作 创建二叉树 一棵二叉树或为空(用 None 表示),或是两棵已有二叉树和要存在树根结点的一项数据,构造起的根结点代表构造出的二叉树: BiTree(dat, left, right) 判断树空:is_empty(bitree) 访问操作,访问二叉树的组成成分: 访问二叉树的根结点数据元素:data() 取得一棵二叉树的左右子树:right(),left() case ... esac 与其他语言中的 switch ... case 语句类似,是一种多分枝选择结构。 case 语句匹配一个值或一个模式,如果匹配成功,执行相匹配的命令。case语句格式如下: case工作方式如上所示。取值后面必须为关键字 in,每一模式必须以右括号结束。取值可以为变量或常数。匹配发现取值符合某一模式后,其间所有命令开始执行直至 ;;。;; 与其他语言中的 break 类似,意思是跳到整个 case 语句的最后。 取值将检测匹配的每一个模式。一旦模式匹配,则执行完匹配模式相应命令后不再继续其他模式。如果无一匹配模式,使用星号 * 捕获该值,再执行后面的命令
1. 树

2. 红黑树

3. 红黑树。。。

4. 红黑树的定义和如何实现的就不要说了,说说红黑树的优点

5. 二叉排序树【左边比根节点小,后边比根节点大】
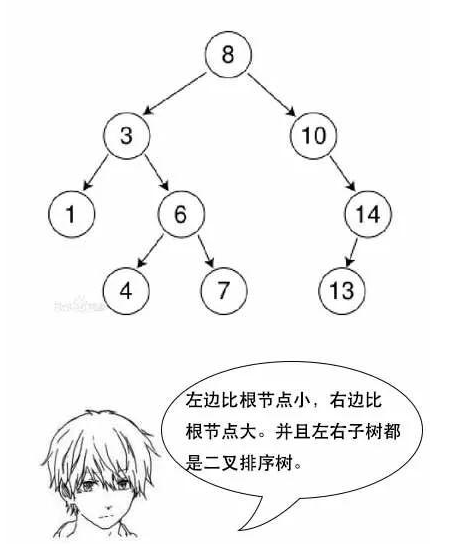
6. 二叉排序树的退化

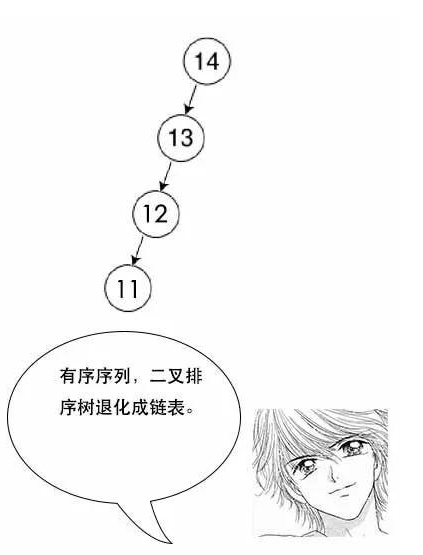

7. 红黑树


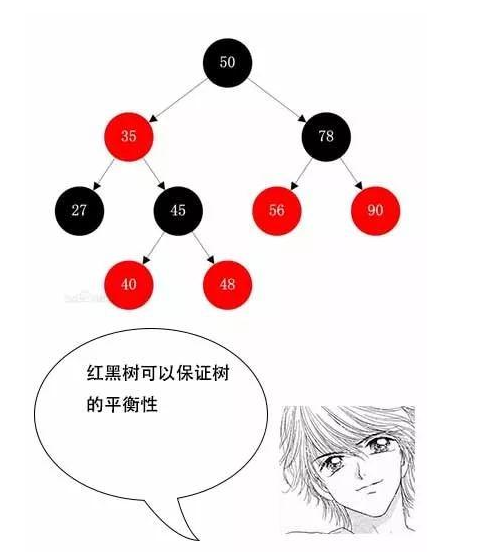
8.因为:



9.B树








10. 文件系统用B树,不用红黑树或别的呢







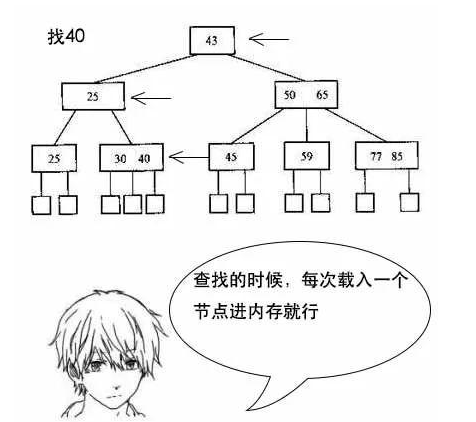

11. B+ 树

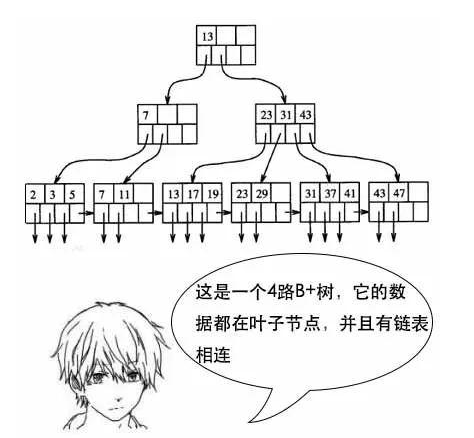



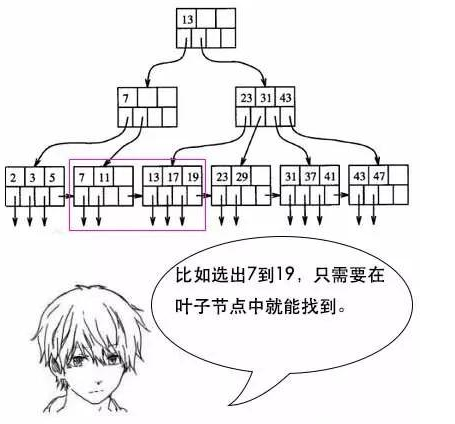
如果是多条的话,B 树需要做局部的中序遍历,可能要跨层访问。
而 B+ 树由于所有数据都在叶子结点,不用跨层,同时由于有链表结构,只需要找到首尾,通过链表就能把所有数据取出来了。
回到现场



 HAHAHA
HAHAHA