本文主要内容:
- 表达式的三种形式
- 中缀表达式与后缀表达式转换算法
一、表达式的三种形式:
- 中缀表达式:运算符放在两个运算对象中间,如:(2+1)*3。我们从小做数学题时,一直使用的就是中缀表达式。
- 后缀表达式:不包含括号,运算符放在两个运算对象的后面,所有的计算按运算符出现的顺序,严格从左向右进行(不再考虑运算符的优先规则),如:2 1 + 3 *。又比如3+(6-4/2)*5=23的后缀表达式为:3642/-5*+# (#符号为结束符)
- 前缀表达式:同后缀表达式一样,不包含括号,运算符放在两个运算对象的前面,如:* + 2 1 3 。前缀表达式和后缀表达式其实是差不多的,只不过符号位置不同而已,前缀表达式不是很常见。
二、中缀表达式转换为后缀表达式:(思路)
1、将中缀表达式转换为后缀表达式:(步骤,有点难理解)
(1)当读到数字直接送至输出队列中;
(2)当读到运算符t时:
a.将栈中所有优先级高于或等于t的运算符弹出,送到输出队列中;
注:这句话不好理解,可以说成这样,从栈顶开始,依次弹出比当前处理的运算符优先级高的运算符,直到一个比它优先级低的或者遇到了一个左括号就停止。
b.t进栈;
(3)读到左括号时总是将它压入栈中;
(4)读到右括号时,将靠近栈顶的第一个左括号上面的运算符全部依次弹出,送至输出队列后,再丢弃左括号;
(5)中缀表达式全部读完后,若栈中仍有运算符,将其送到输出队列中。
举例:
上图中,左侧的那一列为输出序列,右侧的那一列为栈。
2、运用后缀表达式进行计算:
(1)建立一个栈S;
(2)从左到右读后缀表达式,读到数字就将它转换为数值压入栈S中,读到运算符则从栈中依次弹出两个数分别到Y和X,然后以“X 运算符 Y”的形式计算机出结果,再压加栈S中;
(3)如果后缀表达式未读完,就重复上面过程,最后输出栈顶的数值则为结束。
举例:
3+(2-5)*6/3=-3 ,其后缀表达式为:325-6*3/+。其运算结果如下:
三、代码实现:将中缀表达式转换为后缀表达式
- JDK Stack类使用
- 使用泛型
代码实现:
(1)StringToArithmetic.java:(中缀表达式转化为后缀表达式的工具类)
1 /** 2 * Created by smyhvae on 2015/9/7. 3 * 工具类: 4 * 1、中缀表达式转化为后缀表达式 5 * 2、给出一个算术表达式(中缀表达式),直接得到计算结果 6 */ 7 8 import java.util.Stack; 9 import java.util.regex.Pattern; 10 11 public class StringToArithmetic { 12 13 private StringToArithmetic() { 14 } 15 16 //方法:给出一个算术表达式(中缀表达式),得到计算结果。 例如 (5+8+10)*1,返回23 17 public static double stringToArithmetic(String string) { 18 return suffixToArithmetic(infixToSuffix(string)); 19 } 20 21 /** 22 * 中缀表达式转后缀表达式 只处理了+,-,*,/和括号,没有处理负号及其它运算符,也没对前缀表达式验证。 23 * 如要处理负号,可对表达式进行预转义处理,当下面条件成立时,将负号换成单目运算符"!" infix.charAt[i]=='-'&&( 24 * i==0||infix.charAt[i-1]=='(') 25 * 3*6/4+3 26 * 3+6-4 3 6 + 4 - 27 * 3+(6-4/2)*5 3 6 4 2 / - 5 * + 28 */ 29 //方法:中缀表达式转成后缀表达式 30 public static String infixToSuffix(String infix) { 31 Stack<Character> stack = new Stack<Character>(); 32 String suffix = ""; 33 int length = infix.length(); 34 for (int i = 0; i < length; i++) { 35 Character temp; 36 char c = infix.charAt(i); 37 switch (c) { 38 // 忽略空格 39 case ' ': 40 break; 41 // 碰到'(',push到栈 42 case '(': 43 stack.push(c); 44 break; 45 // 碰到'+''-',将栈中所有运算符弹出,送到输出队列中 46 case '+': 47 case '-': 48 while (stack.size() != 0) { 49 temp = stack.pop(); 50 if (temp == '(') { 51 stack.push('('); 52 break; 53 } 54 suffix += " " + temp; 55 } 56 stack.push(c); 57 suffix += " "; 58 break; 59 // 碰到'*''/',将栈中所有乘除运算符弹出,送到输出队列中 60 case '*': 61 case '/': 62 while (stack.size() != 0) { 63 temp = stack.pop(); 64 if (temp == '(' || temp == '+' || temp == '-') { 65 stack.push(temp); 66 break; 67 } else { 68 suffix += " " + temp; 69 } 70 } 71 stack.push(c); 72 suffix += " "; 73 break; 74 // 碰到右括号,将靠近栈顶的第一个左括号上面的运算符全部依次弹出,送至输出队列后,再丢弃左括号 75 case ')': 76 while (stack.size() != 0) { 77 temp = stack.pop(); 78 if (temp == '(') 79 break; 80 else 81 suffix += " " + temp; 82 } 83 // suffix += " "; 84 break; 85 //如果是数字,直接送至输出序列 86 default: 87 suffix += c; 88 } 89 } 90 91 //如果栈不为空,把剩余的运算符依次弹出,送至输出序列。 92 while (stack.size() != 0) { 93 suffix += " " + stack.pop(); 94 } 95 return suffix; 96 } 97 98 99 /** 100 * postfix 101 * 102 * @return double 103 */ 104 //方法:通过后缀表达式求出算术结果 105 public static double suffixToArithmetic(String postfix) { 106 107 Pattern pattern = Pattern.compile("\d+||(\d+\.\d+)"); //使用正则表达式 匹配数字 108 String strings[] = postfix.split(" "); //将字符串转化为字符串数组 109 for (int i = 0; i < strings.length; i++) 110 strings[i].trim(); //去掉字符串首尾的空格 111 Stack<Double> stack = new Stack<Double>(); 112 113 for (int i = 0; i < strings.length; i++) { 114 115 if (strings[i].equals("")) 116 continue; 117 118 //如果是数字,则进栈 119 if ((pattern.matcher(strings[i])).matches()) { 120 121 stack.push(Double.parseDouble(strings[i])); 122 } else { 123 //如果是运算符,弹出运算数,计算结果。 124 double y = stack.pop(); 125 double x = stack.pop(); 126 stack.push(caculate(x, y, strings[i])); //将运算结果重新压入栈。 127 } 128 } 129 return stack.pop(); //弹出栈顶元素就是运算最终结果。 130 131 } 132 133 private static double caculate(double x, double y, String simble) { 134 if (simble.trim().equals("+")) 135 return x + y; 136 if (simble.trim().equals("-")) 137 return x - y; 138 if (simble.trim().equals("*")) 139 return x * y; 140 if (simble.trim().equals("/")) 141 return x / y; 142 return 0; 143 } 144 }
(2)Test.java:(测试类)
1 public class Test { 2 public static void main(String[] args) { 3 4 String str = "3+(2-5)*6/3"; //其后缀表达式为325-6*3/+ 5 6 //调用方法:中缀表达式转成后缀表达式 7 System.out.println(StringToArithmetic.infixToSuffix(str)); 8 9 //调用方法:给出一个算术表达式(中缀表达式),得到计算结果 10 System.out.println(StringToArithmetic.stringToArithmetic(str)); 11 12 } 13 14 }
上方代码中,第07行是根据中缀表达式算出后缀表达式。
第10行:是给出一个中缀表达式,直接的到计算结果,其实它的步骤是:先根据中缀表达式得到后缀表达式,然后根据后缀表达式去计算结果。
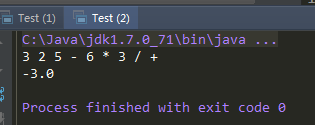
运行效果: