SVM算法 机器学习

目录

梯度下降法、拉格朗日乘子法、KKT条件回顾
感知器模型回顾
SVM线性可分
SVM线性不可分
核函数
SMO

SVM线性可分，SVM线性不可分，核函数，要求会推导

————————————————————————————

 

 

学习率（步长）可以是任何数，如果是二阶偏导数的话，则为牛顿法

 

 优化问题：

　　给定一个目标函数，给定一些约束条件，就构成了一个优化模型。迭代必须是无约束的目标函数才可迭代。

 

 

 对偶问题举例：1、求最小值然后求最大值，转化为求最大值再求最小值。。2、求一个数的最大值转化为求此数的相反数的最小

 KKT条件的三种证明方法对自己看优化问题大有裨益，在此扩展一下

 为了不改变原来的约束条件，β只能>=0，因为β如果大于0的话，g(x)可就<=0不了了。

而要求目标函数L的最小值的话，如果f(x)之后的东西都等于0的话，那么求f(x)的最小值也就是求L的最小值了。，很明显，后面的东西不等于0，既然不等，我们就要想办法证明什么情况下等于0。

因此，证明方式一：βg=0

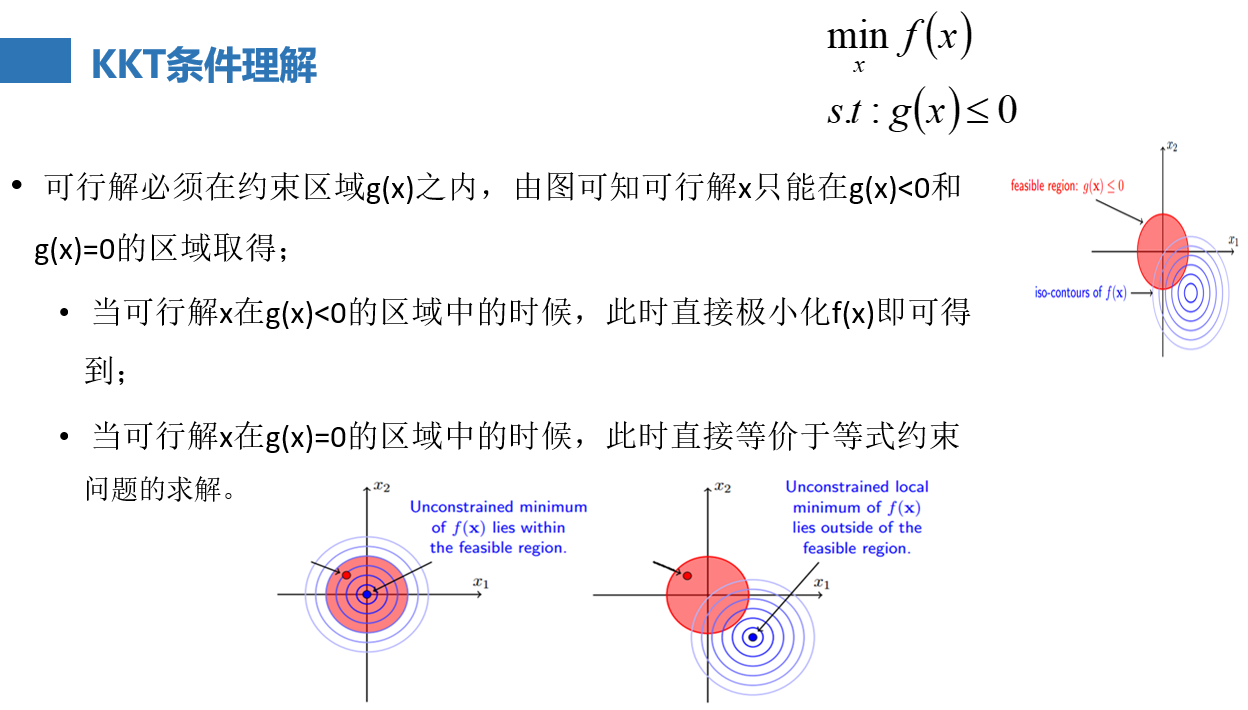
　　如下图，假如 ，一开始不考虑g(x)<=0这个约束条件，只求f(x)的极小值，求极小就是求导等于0，就能得到一个最优解x*,

　　①如果x*代入约束条件g(x)<=0（也就是下图的有g(x)<=0构成的约束区域），恰好小于0，那么说明本来就在约束区域内，既然没有起作用，原函数f(x)后面的东西是不是就是没用的？没用的自然就是0咯，g(x)<0,那么只能是β=0咯

　　②如果x*代入约束条件g(x)<=0后，x*没在约束区域内，它是在区域外（>0）或者在区域边缘(=0)上,大于0不满足咱们的g(x)<=0的约束条件，pass掉，那只能找咱们等于0的时候了，在圆上，那就是g(x*)=0，那完了，g(x)=0了，βg也等于0 了。

　　证明完毕。

 证明方式二：

　　如下图，转化为了从最大值里面挑一个最小值的问题。引入了上界的概念，比如cosx，1,2,3，所有1的倍数都是它的上界，但是1是最小的上界。

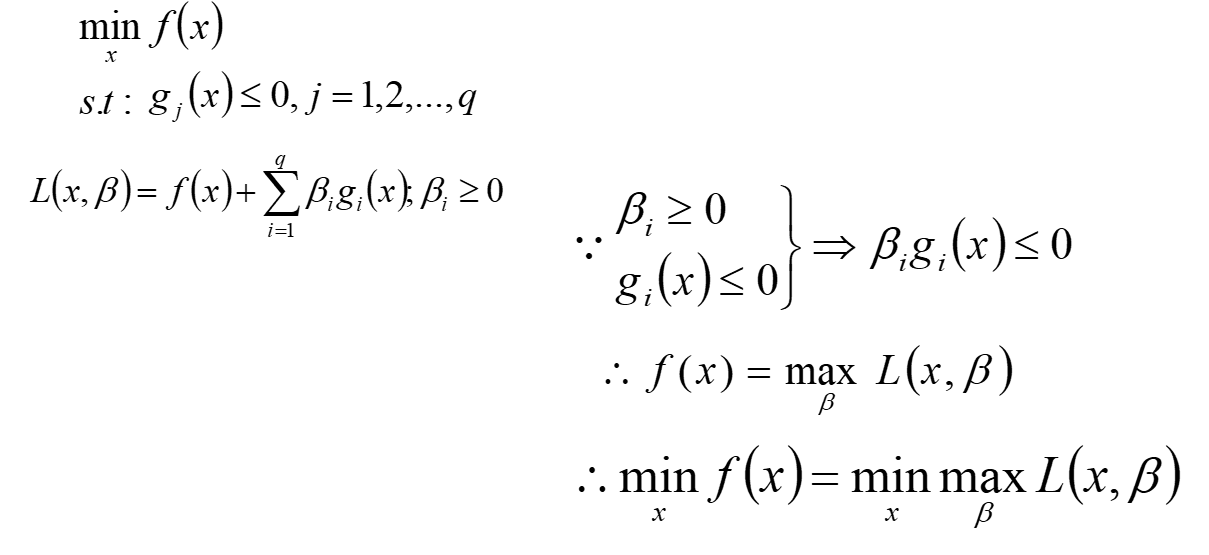
 最终目的是求x与β的，求β最大值可不好求啊，无数个啊朋友们，所以这里用到对偶了，先求最小再 求最大值

 

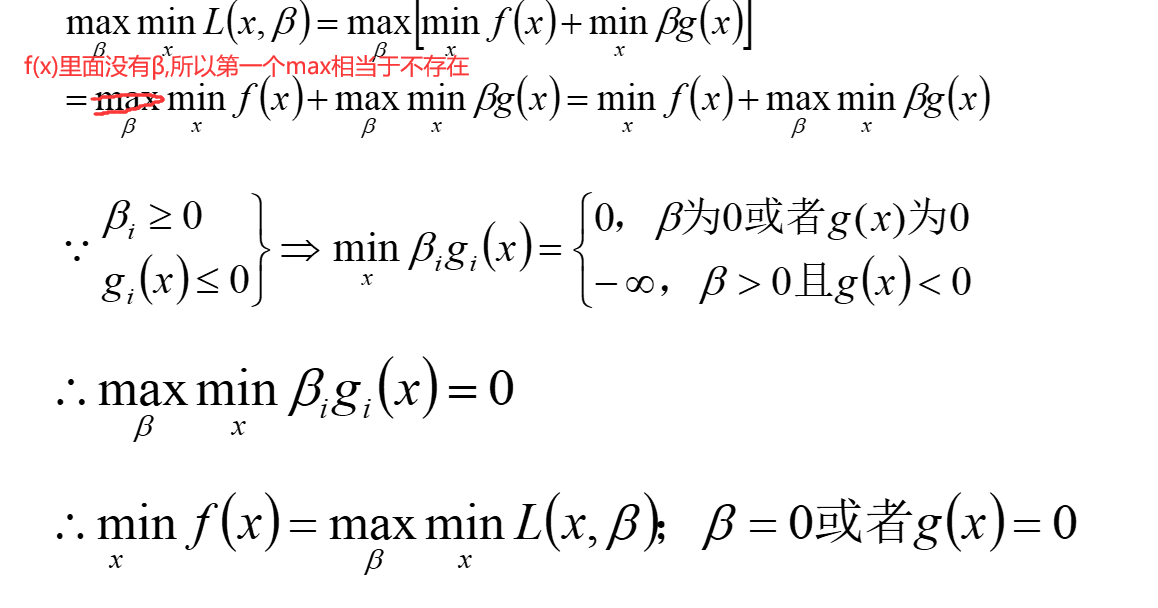
 最后βg=0.

证明方式三：

　　求minf(x),在约束条件g(x)<=0下，加入松弛变量a²,使得g(x)+a²=0，本来是加a的，为了保证它是正的，所以平方了一下。

原函数成了这样：L=f(x)+λ（g(x)+a²）;为了不改变原来的约束条件，λ>=0

接下来求导就可以了

可知 

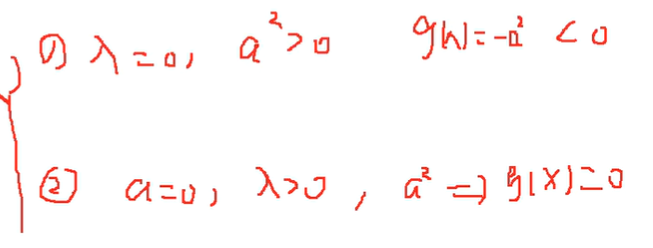
 因此，λg=0

三种证明条件的方法完毕。

所有求不等式的条件：

 感知器模型：

　　感知器算法是最古老的分类算法之一，原理比较简单，不过模型的分类泛化能力比较弱，不过感知器模型是SVM、神经网络、深度学习等算法的基础。
感知器的思想很简单:比如班级有很多的同学，分为男同学和女同学，感知器模型就是试图找到一条直线，能够把所有的男同学和女同学分隔开，
如果是高维空间中，感知器模型寻找的就是一个超平面，能够把所有的二元类别分割开。
感知器模型的前提是:数据是线性可分的

 

 

SVM

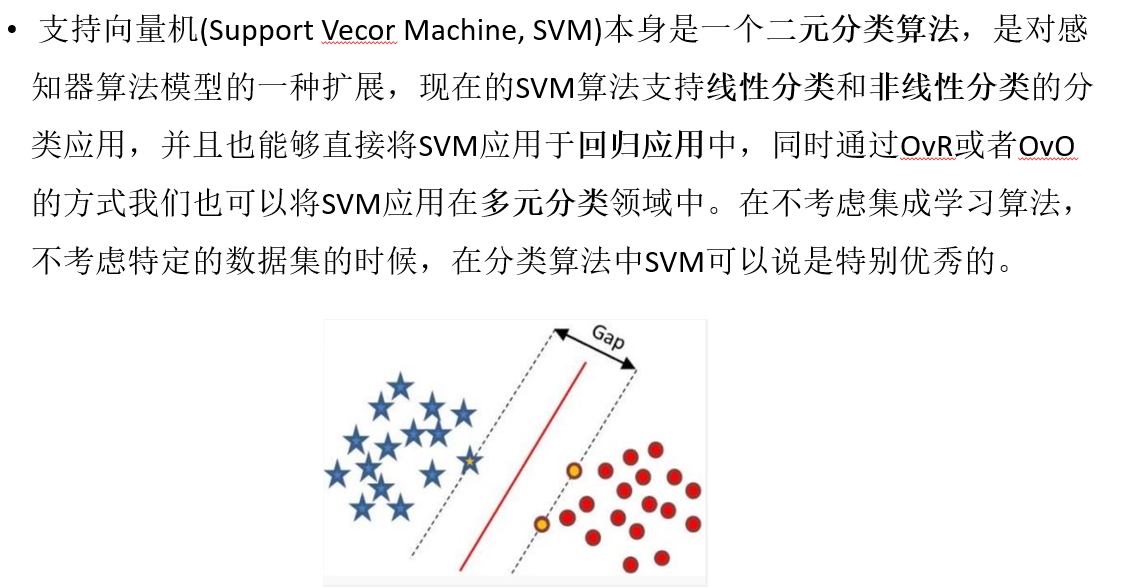
 SVM硬间隔

前提：所有样本均分类正确

目的：在该前提下，搭建一个（让离超平面比较近的点离超平面尽可能的远（也就是最大化硬间隔））的分类器

 

 

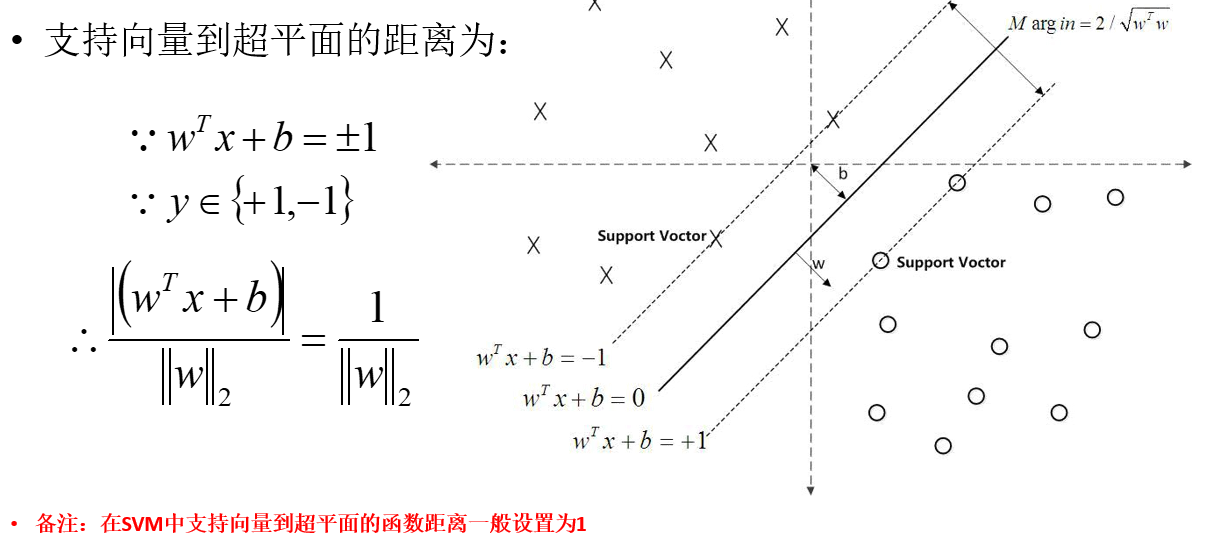
 w^tx+b=0是超平面，假设所有样本都分类正确，设x^s为距离较近的那些点，那么分类正确的离超平面比较近的点要尽可能的离超平面远。w^Tx^s+b/w的二范数为最近的点到超平面的距离，假设w^Tx^s+b的绝对值为1，得到上式

如果所有样本点都分类正确，那么最近的那些点y_iw^Tx^s+b>=0(感知器知识）分对的时候，自然同号。

而y是±1，w^Tx^s+b也是±1，所以，y_iw^Tx^s+b=1，既然最近的那些点=1，那么其他远的点，就是大于1了.

所以其他的远的点就是y_iw^Tx_i+b>=1

 

m个约束条件，引入的超参也就有m个，每个样本都有对应的参数β_i

 

 求J(w)的最小值，找L和J（w）的关系，这部分是<=0的，所以J(w）是L关于β的最大值（只有关于β，其他都是我们要求的参数），求J(w)最小，再套个min就好。

 求最小值，就是求偏导咯

算到这里是用β表示w和b，把这两个表达式代入目标函数L中去，此时还有一个未知参数β

 

那么到这一步最小值求完了，外面还套着一层max,接着求max值

来源于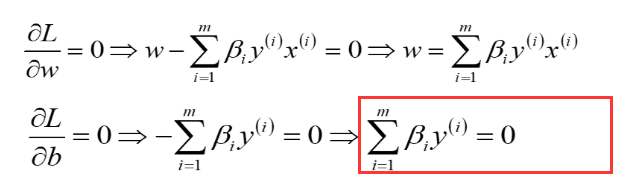，于是把此带进去作为约束条件

 该问题通过一系列转化：

 这里要求的未知参数是m个β值，非常麻烦，所以后续会有SMO算法收拾它

 

 

 

 

 

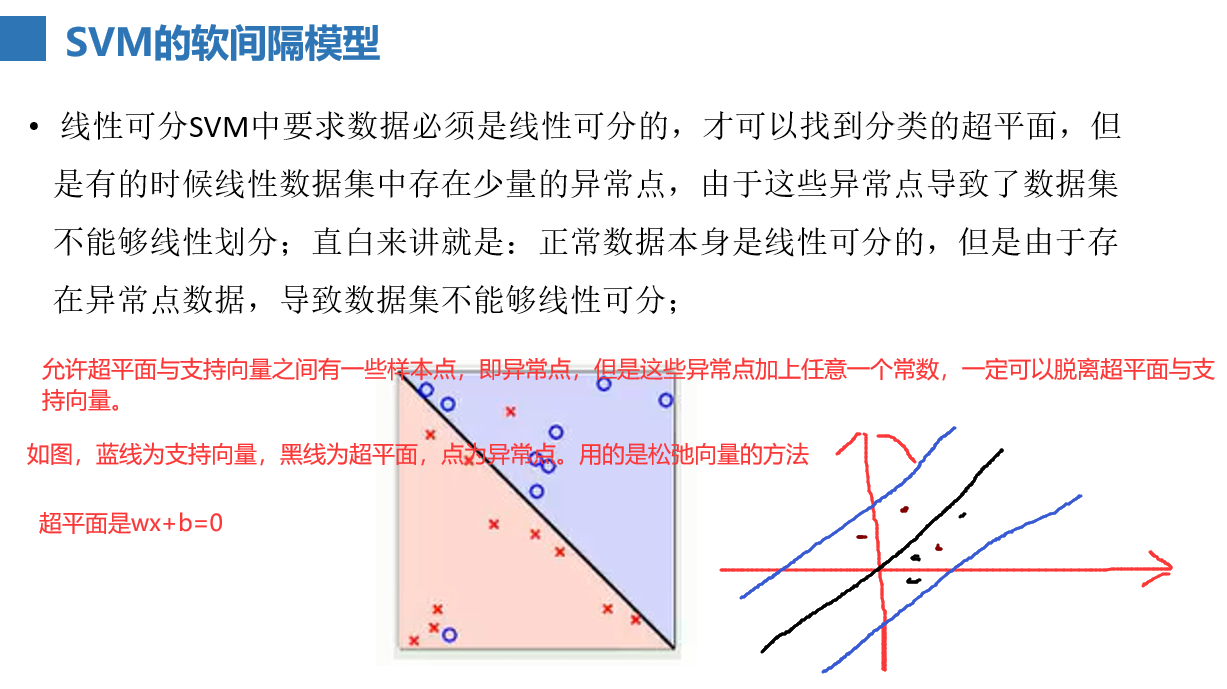
 SVM软间隔

 

 

 

 

 

 

 

 

 

 非线性可分SVM模型

升维后再内积的话维度实在太多太多。我们设法使一个函数来代替升维后的内积，此类函数即为核函数，共三个参数可调，除了图中框起来的，还有相关的系数可调，如下图

 例子：0.8476即为相关的系数，也是第三个可调的参数

 

 

 

 SMO算法

核心原理：迭代与优化原理：θ^new=f(θ^old),用自己，表示自己

　　　　　　　　　　　　　θ^new-θ^old=Δθ

作用：求下列约束优化问题的最优解β^*

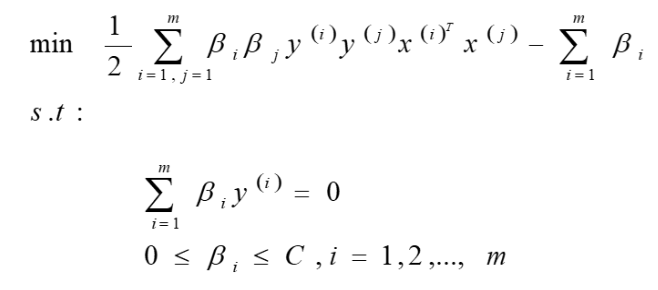等价于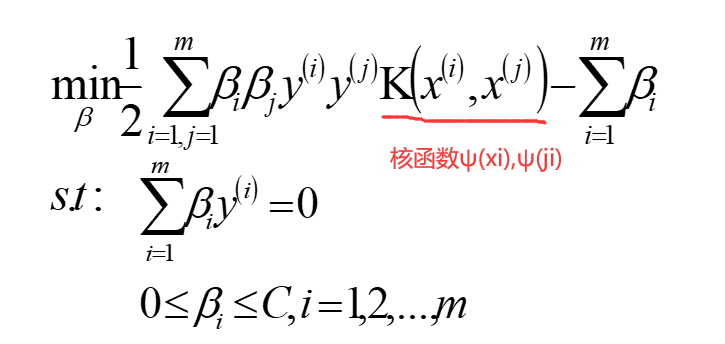

 分离超平面为g(x)=w^Tx+b

推导过程太复杂，不再作多阐述，这里给出结果与算法的实现

 

SMO不适合大批量数据，参数太多，计算太复杂

 SVR算法其实就是线性回归的对偶问题，本质还是线性回归问题罢了