间隔与支持向量
1. 样本集 \( D = \{ (x_1,y_1), (x_2,y_2), ..., (x_m,y_m) \} \),\( x \in R^d \),\( y \in \{-1, +1\} \) 线性可分。支持向量机在几何上的含义就是,由法向量 $ w $ 和偏移 $ b $ 唯一确定的超平面 \( f(x) = w^T x + b = 0 \),\( w = ( w_1; w_2; ...; w_d ) \) 在 “正中间” 划分样本集。也即是,该给定超平面,就构成了一个同样由两个参数 $ w $ 和 $ b $ 唯一确定的二分类判别器 \( D(w, b) := sign(y(x)) = sign(w^T x + b) \)。任意一点 $ x $,\( f(x) > 0 \) 时判定为正例,\( f(x) < 0 \) 时判定为反例。
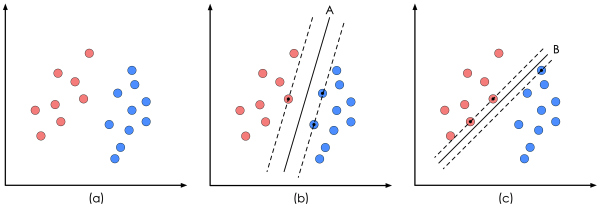
2. 对于一个由法向量 $ w $ 和偏移 $ b $ 确定的超平面,假设样本点 $ x_i $ 到该给定超平面的距离为 $ r(x_i) $。那么,由于 \( x_i - r(x_i) \frac {w}{ |w| } \) 点在该超平面上,所以,通过代入超平面的公式 \( f(x) = w^T x + b = 0 \) 中,得距离 \( r(x_i) = \frac { |w^T x_i + b| }{ \| w \| } \)。称于所有样本点中,距离该超平面最近的,两种异类的样本点为 “支持向量”:\( x_{sv} = \underset{x_i}{\operatorname{min}} r(x_i) \);并且,称异类的 “支持向量” 所构成的 “支撑面” 之间的距离为 “间隔”: \( \gamma(w, b) = \underset{x_i}{\operatorname{\mathop{\min}}} 2 r(x_i)\ = \underset{x_i}{\operatorname{\mathop{\min}}}\ 2 \frac { |w^T x_i + b| }{ \| w \| } \)。支持向量机认为,与样本集的 “间隔” 最大的超平面所构成的分类器是最好的:\( \underset{w, b}{\operatorname{\mathop{\max}}} \gamma(w, b) = \underset{w, b}{\operatorname{\mathop{\max}}} \underset{x_i}{\operatorname{\mathop{\min}}}\ 2 \frac { |w^T x_i + b| }{ \| w \| } \)。以及,条件是正确划分所有样本点:\( y_i (w^T x_i + b) \ge 0, i = 1,2,...,m \)。
P.S. 在 “支持向量机” 这个名字中,向量意味着样本点 $ x $ 是多($ x \in R^d $)维的;支持意味着经过该 “支持向量” 的超平面 “勉强” 能够将样本集正确划分,因此说 “支持向量” 支撑着能正确划分样本集的超平面;在最后,通过推导可以看出,决定该超平面的参数 $ w $ 和 $ b $ 可以通过为数不多的几个 “支持向量” 确定。
3. 该优化问题可以化简如下:
\( \underset{w, b}{\operatorname{\mathop{\max}}} \underset{x_i}{\operatorname{\mathop{\min}}} 2 \frac { |w^T x_i + b| }{ \| w \| }\ \ s.t.\ y_i (w^T x_i + b) \ge 0, i = 1,2,...,m \)
\( \Leftrightarrow\ \underset{w, b}{\operatorname{\mathop{\max}}} \frac{2}{\| w \|}\ \underset{x_i}{\operatorname{\mathop{\min}}} y_i (w^T x_i + b)\ \ s.t.\ y_i (w^T x_i + b) \ge 0, i = 1,2,...,m \)
\( \Leftrightarrow\ \underset{w, b}{\operatorname{\mathop{\max}}} \frac{2}{ \|w\| }\ \ s.t.\ y_i (w^T x_i + b) \ge 1, i = 1,2,...,m\ \ \because \exists\ w, b\ \underset{x_i}{\operatorname{\mathop{\min}}}\ y_i (w^T x_i + b) = 1 \)
\( \Leftrightarrow\ \underset{w, b}{\operatorname{\mathop{\min}}} \frac{ \|w\|^2 }{2}\ \ s.t.\ y_i (w^T x_i + b) \ge 1, i = 1,2,...,m\ \)
对第三步的解释是,缩放参数 $ w $ 和 $ b $ 相同的倍数,超平面不变,任意一点到该超平面的距离 $ r(x) $ 也不变。因此,可以同时缩放这两个参数,使 \( \frac{2}{|w|} = \Gamma(w, b) \) ,也就是 \( \forall\ x_i\ r(x_i) \ge \frac{\Gamma(w, b)}{2} = \frac{1}{|w|} \),即 \( \forall\ x_i\ |w^T x + b| \ge 1 \),这是为了令 \( \frac{2}{|w|} = \gamma(w, b) \),所有的样本点需要满足的条件。
对偶问题
1. 到此为止,已经将线性可分的支持向量机的思想,转化为求解一个含有不等式约束的凸优化问题。但是,为了推广到非线性分类上,要依靠 对偶问题 与 核函数 来简化后续的复杂计算。引入拉格朗日算子:\( L(w, b, \alpha) = \frac{1}{2} w^T w + \sum_{i=1}^{m} \alpha_i (1 - y_i (w^T x_i + b))\ \operatorname{s.t.}\ \alpha_i \ge 0,\ i = 1, 2, ..., m \),有:
\( \underset{w, b}{\operatorname{\mathop{\min}}} \frac{ \|w\|^2 }{2}\ \ s.t.\ y_i (w^T x_i + b) \ge 1, i = 1,2,...,m\ \Leftrightarrow\ \underset{w, b}{\operatorname{\mathop{\min}}} \underset{\alpha: \alpha \ge 0}{\operatorname{\mathop{\max}}} L(w, b, \alpha) \)
\( \Delta \overset{let}{=} (1 - y_i (w^T x_i + b)) \),\( \because\ \begin{equation} \begin{cases} if\ \Delta>0\ \underset{\alpha: \alpha \ge 0}{\operatorname{\mathop{\max}}} L(w, b, \alpha) = \infty,\\ if\ \Delta \le 0\ \underset{\alpha: \alpha \ge 0}{\operatorname{\mathop{\max}}} L(w, b, \alpha) = \frac{1}{2} w^T w.\\ \end{cases} \end{equation}\)
\( \therefore\ \underset{w, b}{\operatorname{\mathop{\min}}} \underset{\alpha}{\operatorname{\mathop{\max}}} L(w, b, \alpha) = \underset{w}{\operatorname{\mathop{\min}}} \{ \infty, \frac{1}{2} w^T w \} = \underset{w}{\operatorname{\mathop{\min}}} \frac{1}{2} w^T w \)
2. 又因为,在凸优化理论中,该问题满足 “强对偶” 条件,证明略。所以,以上的原问题,又等价于其对偶问题:\( \max_{\alpha: \alpha \ge 0} \min_{w, b}\ L(w, b, \alpha) \)。其中,可以先解出无约束问题 \( \theta_D(\alpha) = \underset{w, b}{\operatorname{\mathop{\min}}}\ L(w, b, \alpha) \):令 \( L(w, b, \alpha) \) 对 $ w $ 和 $ b $ 的偏导为零,可得:\( w = \sum_{i=1}^{m} \alpha_i y_i x_i \) 以及 \( 0 = \sum_{i=0}^{m} \alpha_i y_i \)。代入拉格朗日算子,化简其为一个只关于变量 $ \alpha $ 的凸二次规划问题:\( \underset{\alpha }{\mathop{\max}}\, \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i=1, j=1}^{m} \alpha_i \alpha_j y_i y_j x_i^T x_j \ s.t. \alpha_i \ge 0,\ \sum_{i=1}^{m} \alpha_i y^i = 0,\ i = 1, 2, ..., m \),问题的规模和样本数 $ m $ 相关,使用序列最小优化 SMO 算法可以减小降低计算的开销;以及,带入分类模型,化简其为:\( f(x) = w^T x + b = \sum_{i=1}^{m} \alpha_i y^i x_i^T x + b \);可见,在要优化的目标函数,以及最终得到的分类模型中,只有 $ \alpha_i \ne 0 $ 的项才发挥作用。恰好,因为原问题含有不等式约束 ,也就需要满足松弛互补 \( \alpha_i (y_i f(x_i) - 1) = 0 \) 等 KKT 条件,据此,$ \alpha_i \ne 0 $ 所对应的样本点 \( (x_i, y_i) \) 需要满足 $ y_i (w^T x_i + b) = y_i f(x_i) = 1 $,这也就是在原问题的约束下,“支持向量” 满足的条件。如果用序号 $ _{sv} $ 表示任意一个满足该条件的样本点的序号,那么,有 $ w = \sum_{x_{sv}} \alpha_{sv} y_{sv} x_{sv} $,以及 $ y_{sv}^2 (w^T x_{sv} + b) = w^T x_{sv} + b = y_{sv}.\ \Rightarrow\ b = y_{sv} - w^T x_{sv} = y_{sv} - \sum_{x_{sv}} \alpha_{sv} y_{sv} x_{sv}^T x_{sv} $。可以说,在训练结束以后,大部分样本都可以丢掉了,最终模型实际上只与 "支持向量" \( x_{sv} \) 有关系,而法向量 $ w $ 是 “支持向量” $ x_{sv} $ 的线性组合。
其他
1. 在上诉过程中,数据的特征 $ x $ 往往需要借助一个函数 $ \phi(\cdot) $ 映射到高纬度,使得数据集线性可分。这样做的结果是,造成 “维度爆炸” 的问题。具体地,由于需要计算特征向量的内积,因此,如果使用的高维映射函数将向量的长度从 $ n $ 变成 $ n^2 $,那么,解中的 $ \phi(v)^T \phi(w) $ 计算复杂度为 $ O(n^2) $。而核函数 $ k(\cdot, \cdot) $ 的作用,就是通过化简这里的向量内积,比如说,重新变回原来 $ v^T w $ 的计算复杂度 $ O(n) $,使得计算复杂度大大降低。也就是说,如果存在一个核函数使得 $ k(v, w) = \phi(v)^T \phi(w) $,而等式左边复杂度远远低于右边,就达到了化简的目的。这样的核函数有高斯核函数等,证明一个函数是否是核函数也有相应的定理。2. 另外,有时候,即使使用了核函数,也还是无法满足绝对的线性可分,以及,为了防止过拟合,允许一定的误差。此时,称加入误差的间隔为软间隔。并新增对该机制的惩罚项,即其正则化。3. 在具体计算以 $ \alpha $ 为变量的优化问题时,可以使用坐标上升算法,又因为该变量有一个等式约束,因而可以使用同时调整两个维度的方式进行更新,该算法就是序列最小优化 SMO 算法,“最小” 表示每次需要更新的最少参数个数,也就是两个维度。
参考:
1. 周志华-机器学习-第 6 章-支持向量机;
2. 吴恩达-斯坦福公开课-CS229-支持向量机;
3. shuhuai007-机器学习-白板推导系列-支持向量机;
4. 优化方法笔记:拉格朗日乘子法 与 KKT 条件 以及 对偶问题;