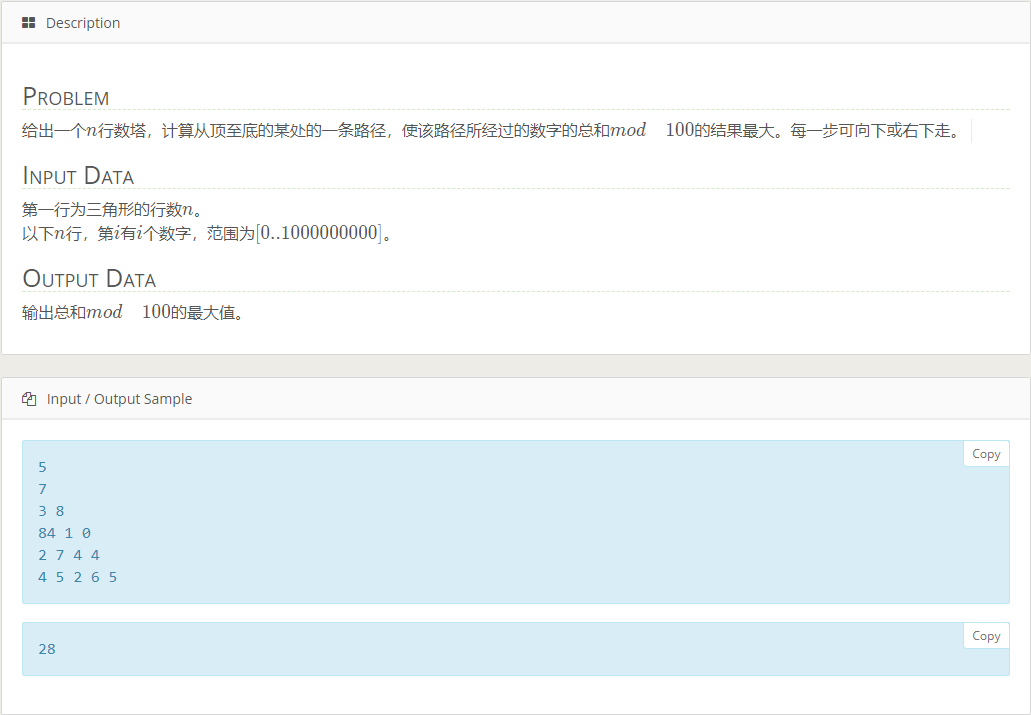
看一下题目 和普通的数字三角形看似没啥区别(区别很大)
然后去想:DP方程
DP[i][j]=Max(DP[i-1][j],DP[i-1][j-1])+a[i][j] ans=Max(DP[n][1..n])
这是普通的数字三角形的方程。。。然后你会发现跟这道题没啥直接关系
主要是这道题目比较毒瘤 因为 有的时候局部最优≠全局最优
所以...这题 仔细一看 mod 100 就说明了 余数 肯定<100
然而 动态规划的每一维都是表示状态。。
这里用到3个状态。 x,y,w(自然就是三维)
#include <bits/stdc++.h> #define rep(i,j,n) for(register int i=j;i<=n;i++) using namespace std; typedef long long LL; inline LL read() { LL x=0; int f=1; char ch=getchar(); while(!isdigit(ch)) { if (ch=='-') f=-1; ch=getchar();} while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); return x*f; } int n; const int N=1<<7; const int mod=100; LL a[N][N]; bool DP[N][N][N]; signed main(){ n=read(); rep(i,1,n) rep(j,1,i) a[i][j]=read()%mod; DP[1][1][a[1][1]]=1; rep(i,1,n) rep(j,1,i) rep(k,0,99) if(DP[i][j][k]) { DP[i+1][j][(k+a[i+1][j])%mod]=1; DP[i+1][j+1][(k+a[i+1][j+1])%mod]=1; } for(register int k=99;k>=0;k--) rep(i,1,n) if(DP[n][i][k]) { cout << k << endl ; return 0; } }
时间复杂度大概就是(100*n2)