欢迎大家前往腾讯云技术社区，获取更多腾讯海量技术实践干货哦~
作者：汪毅雄
导语 本文用容易理解的语言和例子来解释了决策树三种常见的算法及其优劣、随机森林的含义，相信能帮助初学者真正地理解相关知识。
决策树
引言
决策树，是机器学习中一种非常常见的分类方法，也可以说是所有算法中最直观也最好理解的算法。先举个最简单的例子：
A：你去不去吃饭？
B：你去我就去。
“你去我就去”，这是典型的决策树思想。
再举个例子：
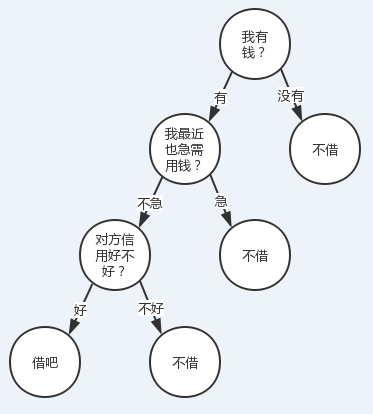
有人找我借钱（当然不太可能。。。），借还是不借？我会结合根据我自己有没有钱、我自己用不用钱、对方信用好不好这三个特征来决定我的答案。
我们把转到更普遍一点的视角，对于一些有特征的数据，如果我们能够有这么一颗决策树，我们也就能非常容易地预测样本的结论。所以问题就转换成怎么求一颗合适的决策树，也就是怎么对这些特征进行排序。
在对特征排序前先设想一下，对某一个特征进行决策时，我们肯定希望分类后样本的纯度越高越好，也就是说分支结点的样本尽可能属于同一类别。
所以在选择根节点的时候，我们应该选择能够使得“分支结点纯度最高”的那个特征。在处理完根节点后，对于其分支节点，继续套用根节点的思想不断递归，这样就能形成一颗树。这其实也是贪心算法的基本思想。那怎么量化“纯度最高”呢？熵就当仁不让了，它是我们最常用的度量纯度的指标。其数学表达式如下：
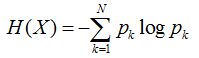
其中N表示结论有多少种可能取值，p表示在取第k个值的时候发生的概率，对于样本而言就是发生的频率/总个数。
熵越小，说明样本越纯。
以一个两点分布样本X（x=0或1）的熵的函数图像来说明吧，横坐标表示样本值为1的概率，纵坐标表示熵。
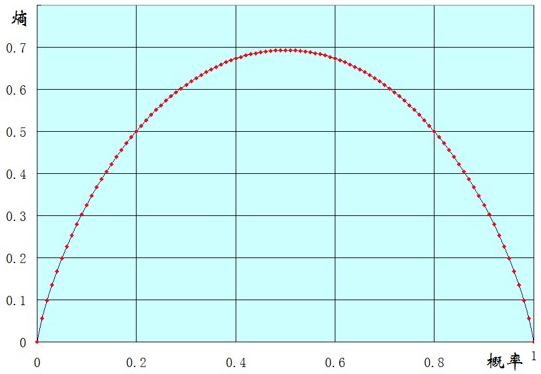
可以看到到当p（x=1）=0时，也就是说所有的样本都为0，此时熵为0.
当p（x=1）=1时，也就是说所有的样本都为1，熵也为0.
当p（x=1）=0.5时，也就是样本中0，1各占一半，此时熵能取得最大值。
扩展一下，样本X可能取值为n种（x1。。。。xn）。可以证明，当p（xi）都等于1/n 时，也就是样本绝对均匀，熵能达到最大。当p（xi）有一个为1，其他都为0时，也就是样本取值都是xi，熵最小。
决策树算法
ID3
假设在样本集X中，对于一个特征a，它可能有（a1，a2。。。an）这些取值，如果用特征a对样本集X进行划分（把它当根节点），肯定会有n个分支结点。刚才提了，我们希望划分后，分支结点的样本越纯越好，也就是分支结点的“总熵”越小越好。
因为每个分支结点的个数不一样，因此我们计算“总熵”时应该做一个加权，假设第i个结点样本个数为W(ai)，其在所有样本中的权值为W(ai) / W(X)。所以我们可以得到一个总熵：
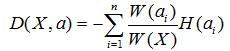
这个公式代表含义一句话：加权后各个结点的熵的总和。这个值应该越小，纯度越高。
这时候，我们引入一个名词叫信息增益G（X，a），意思就是a这个特征给样本带来的信息的提升。公式就是：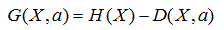
，由于H(X)对一个样本而言，是一个固定值，因此信息增益G应该越大越好。寻找使得信息增益最大的特征作为目标结点，并逐步递归构建树，这就是ID3算法的思想，
好了以一个简单的例子来说明信息增益的计算：
上面的例子，我计算一下特征1的信息增益
首先计算样本的熵H（X）
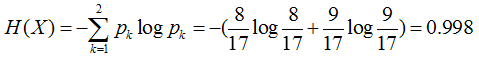
再计算总熵，可以看到特征1有3个结点A、B、C，其分别为6个、6个、5个
所以A的权值为6/(6+6+5), B的权值为6/(6+6+5), C的为5/(6+6+5)
因为我们希望划分后结点的纯度越高越好，因此还需要再分别计算结点A、B、C的熵
特征1=A：3个是、3个否，其熵为
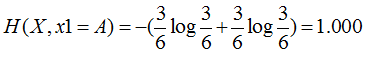
特征1=B：2个是、4个否，其熵为
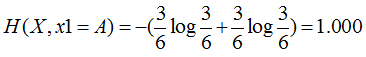
特征1=C：4个是、1个否，其熵为
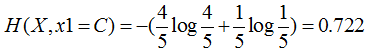
这样分支结点的总熵就等于：
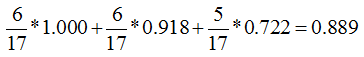
特征1的信息增益就等于0.998-0.889=0.109
类似地，我们也能算出其他的特征的信息增益，最终取信息增益最大的特征作为根节点。
以上计算也可以有经验条件熵来推导：G（X,A）=H(X) - H(X|A)，这部分有兴趣的同学可以了解一下。
C4.5
在ID3算法中其实有个很明显的问题。
如果有一个样本集，它有一个叫id或者姓名之类的（唯一的）的特征，那就完蛋了。设想一下，如果有n个样本，id这个特征肯定会把这个样本也分成n份，也就是有n个结点，每个结点只有一个值，那每个结点的熵就为0。就是说所有分支结点的总熵为0，那么这个特征的信息增益一定会达到最大值。因此如果此时用ID3作为决策树算法，根节点必然是id这个特征。但是显然这是不合理的。。。
当然上面说的是极限情况，一般情况下，如果一个特征对样本划分的过于稀疏，这个也是不合理的（换句话就是，偏向更多取值的特征）。为了解决这个问题，C4.5算法采用了信息增益率来作为特征选取标准。
所谓信息增益率，是在信息增益基础上，除了一项split information,来惩罚值更多的属性。
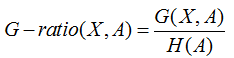
而这个split information其实就是特征个数的熵H（A）。
为什么这样可以减少呢，以上面id的例子来理解一下。如果id把n个样本分成了n份，那id这个特征的取值的概率都是1/n，文章引言已经说了，样本绝对均匀的时候，熵最大。
因此这种情况，以id为特征，虽然信息增益最大，但是惩罚因子split information也最大，以此来拉低其增益率，这就是C4.5的思想。
CART
决策树的目的最终还是寻找到区分样本的纯度的量化标准。在CART决策树中，采用的是基尼指数来作为其衡量标准。基尼系数直观的理解是，从集合中随机抽取两个样本，如果样本集合越纯，取到不同样本的概率越小。这个概率反应的就是基尼系数。
因此如果一个样本有K个分类。假设样本的某一个特征a有n个取值的话，其某一个结点取到不同样本的概率为：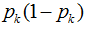
因此k个分类的概率总和，我们称之为基尼系数：
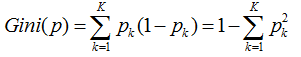
而基尼指数，则是对所有结点的基尼系数进行加权处理
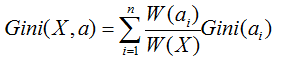
计算出来后，我们会选择基尼系数最小的那个特征作为最优划分特征。
剪枝
剪枝的目的其实就是防止过拟合，它是决策树防止过拟合的最主要手段。决策树中，为了尽可能争取的分类训练样本，所以我们的决策树也会一直生长。但是呢，有时候训练样本可能会学的太好，以至于把某些样本的特有属性当成一般属性。这时候就我们就需要主动去除一些分支，来降低过拟合的风险。
剪枝一般有两种方式：预剪枝和后剪枝。
预剪枝
一般情况下，只要结点样本已经100%纯了，树才会停止生长。但这个可能会产生过拟合，因此我们没有必要让它100%生长，所以在这之前，设定一些终止条件来提前终止它。这就叫预剪枝，这个过程发生在决策树生成之前。
一般我们预剪枝的手段有：
1、限定树的深度
2、节点的子节点数目小于阈值
3、设定结点熵的阈值
等等。
后剪枝
顾名思义，这个剪枝是在决策树建立过程后。后剪枝算法的算法很多，有些也挺深奥，这里提一个简单的算法的思想，就不深究啦。
Reduced-Error Pruning (REP)
该剪枝方法考虑将树上的每个节点都作为修剪的候选对象，但是有一些条件决定是否修剪，通常有这几步：
1、删除其所有的子树，使其成为叶节点。
2、赋予该节点最关联的分类
3、用验证数据验证其准确度与处理前比较
如果不比原来差，则真正删除其子树。然后反复从下往上对结点处理。这个处理方式其实是处理掉那些“有害”的节点。
随机森林
随机森林的理论其实和决策树本身不应该牵扯在一起，决策树只能作为其思想的一种算法。
为什么要引入随机森林呢。我们知道，同一批数据，我们只能产生一颗决策树，这个变化就比较单一了。还有要用多个算法的结合呢？
这就有了集成学习的概念。
图中可以看到，每个个体学习器（弱学习器）都可包含一种算法，算法可以相同也可以不同。如果相同，我们把它叫做同质集成，反之则为异质。
随机森林则是集成学习采用基于bagging策略的一个特例。
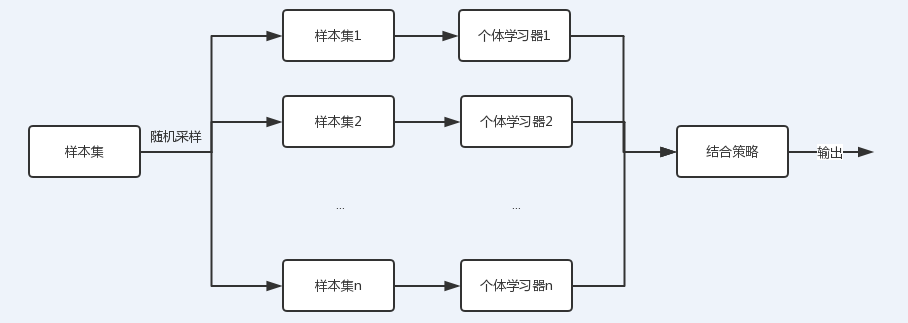
从上图可以看出，bagging的个体学习器的训练集是通过随机采样得到的。通过n次的随机采样，我们就可以得到n个样本集。对于这n个样本集，我们可以分别独立的训练出n个个体学习器，再对这n个个体学习器通过集合策略来得到最终的输出，这n个个体学习器之间是相互独立的，可以并行。
注：集成学习还有另一种方式叫boosting，这种方式学习器之间存在强关联，有兴趣的可以了解下。
随机森林采用的采样方法一般是是Bootstap sampling，对于原始样本集，我们每次先随机采集一个样本放入采样集，然后放回，也就是说下次采样时该样本仍有可能被采集到，经过一定数量的采样后得到一个样本集。由于是随机采样，这样每次的采样集是和原始样本集不同的，和其他采样集也是不同的，这样得到的个体学习器也是不同的。
随机森林最主要的问题是有了n个结果，怎么设定结合策略，主要方式也有这么几种：
加权平均法：
平均法常用于回归。做法就是，先对每个学习器都有一个事先设定的权值wi，
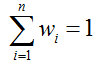
然后最终的输出就是：
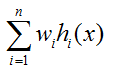
当学习器的权值都为1/n时，这个平均法叫简单平均法。
投票法：
投票法类似我们生活中的投票，如果每个学习器的权值都是一样的。
那么有绝对投票法，也就是票数过半。相对投票法，少数服从多数。
如果有加权，依然是少数服从多数，只不过这里面的数是加权后的。
例子
以一个简单的二次函数的代码来看看决策树怎么用吧。
训练数据是100个随机的真实的平方数据，不同的深度将会得到不同的曲线
测试数据也是随机数据，但是不同深度的树的模型，产生的预测值也不太一样。如图
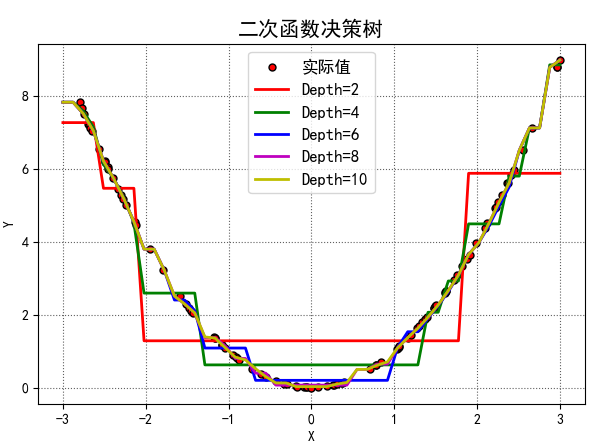
这幅图的代码如下：
我的是python 3.6环境，需要安装numpy、matplotlib、sklearn这三个库，需要的话直接pip install，大家可以跑跑看看，虽然简单但挺有趣。
#!/usr/bin/python # -*- coding:utf-8 -*- import numpy as np import matplotlib as mpl import matplotlib.pyplot as plt from sklearn.tree import DecisionTreeRegressor if __name__ == "__main__": # 准备训练数据 N = 100 x = np.random.rand(N) * 6 - 3 x.sort() y = x*x x = x.reshape(-1, 1) mpl.rcParams['font.sans-serif'] = ['SimHei'] mpl.rcParams['axes.unicode_minus'] = False # 决策树深度及其曲线颜色 depth = [2, 4, 6, 8, 10] clr = 'rgbmy' # 实际值 plt.figure(facecolor='w') plt.plot(x, y, 'ro', ms=5, mec='k', label='实际值') # 准备测试数据 x_test = np.linspace(-3, 3, 50).reshape(-1, 1) # 构建决策树 dtr = DecisionTreeRegressor() # 循环不同深度情况下决策树的模型，并用之测试数据的输出 for d, c in zip(depth, clr): # 设置最大深度（预剪枝） dtr.set_params(max_depth=d) # 训练决策树 dtr.fit(x, y) # 用训练数据得到的模型来验证测试数据 y_hat = dtr.predict(x_test) # 画出模型得到的曲线 plt.plot(x_test, y_hat, '-', color=c, linewidth=2, markeredgecolor='k', label='Depth=%d' % d) # 一些画图的基本参数 plt.legend(loc='upper center', fontsize=12) plt.xlabel('X') plt.ylabel('Y') plt.grid(b=True, ls=':', color='#606060') plt.title('二次函数决策树', fontsize=15) plt.tight_layout(2) plt.show()
参考资料
机器学习 周志华
机器学习课程 邹博
相关阅读
道器相融，由 Angel 谈一个优秀机器学习平台的自我修养（下）
此文已由作者授权腾讯云技术社区发布，转载请注明文章出处
原文链接：https://www.qcloud.com/community/article/160232