0 目录
凡 AI 类的落地，都需要具备这几个基本元素才行：数据、算法、场景、计算力。
本专栏分成五个模块：
1 概念篇：推荐系统的理念、思考、形而上的内容；
2 原理篇：推荐算法的原理介绍；
3 工程篇：推荐算法的实践内容；
4 产品篇：考虑产品理念及其商业价值；
5 团队篇：讨论个人学习和成长；团队合作等问题。
1 概念篇
2 原理篇
2.1 内容推荐
2.2 邻近推荐
2.2.2.1 基于用户的协同过滤
找到相似的人购买过的物品，从而推荐给你。关键在于量化相似性
原理：
1）建立关系矩阵，准备每个用户的稀疏向量，维度就是物品的个数
2）用户两两之间计算相似度，保留与其最相似的几个用户。
2.1）解决物品数或用户量很大的方法是降采样、向量化计算、Map Reduce
2.2）相似度，计算两向量之间的夹角，越相似夹角越小
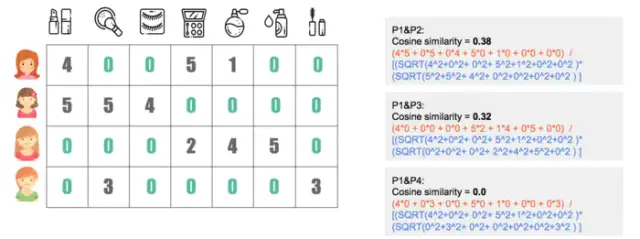
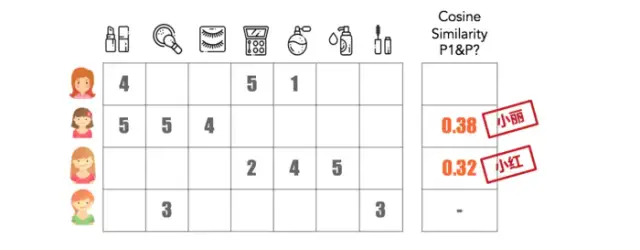
3） 推荐计算，为每个用户产生推荐结果
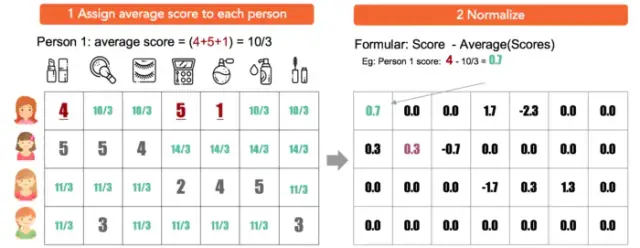
改进1：在第二步中标准化评分，而不是填0
2.2.2.2 基于物品的协同过滤
1）建立与上述转置的关系矩阵
2）按照基于用户的协同过滤方法计算物品之间的相似度，并保留TopK
3）推荐计算，待推荐物品的评分
差别：
相对于基于用户的协同过滤，基于物品的协同过滤，
1）在物品数量上会比用户少，计算量减少
2）物品之间的相似度比较静态，更换没有用户口味这么快
改进：都是对关系矩阵中分值的量化和相似度的计算
1）物品中心化：抑制铁粉的物品打分
2）用户中心化：标准化每个用户打分不同的标准
2.2.2.3 相似度计算方法
1）欧氏距离，把范围为 0 到正无穷的欧式距离转换为 0 到 1 的相似度
2）调整的余弦相似度，是先计算向量每个维度上的均值，然后每个向量在各个维度上都减去均值后，再计算余弦相似度
3）皮尔逊相关度，向量 p 和 q 各自 减去向量的均值后，再计算余弦相似度
4）杰卡德（Jaccard）相似度，是两个集合的交集元素个数在并集中所占的比例
1. 分子是两个布尔向量做点积计算，得到的就是交集元素个数； 2. 分母是两个布尔向量做或运算，再求元素和。
余弦相似度适用于评分数据，杰卡德相似度适合用于隐式反馈数据。例如，使用用户的收藏行为，计算用户之间的相似度，杰卡德相似度就适合来承担这个任务。
矩阵分解 SVD：评分预测
适用对象：具有评分数据的预测问题
为什么要矩阵分解
近邻推荐存在的问题：
（1）物品之间存在相关性，信息量并不随着向量维度增加而线性增加，而是大于线性的增加；
（2）矩阵元素稀疏，计算结果不稳定，增减一个向量维度，导致近邻结果差异很大的情况存在。
为了解决上述问题，矩阵分解可以解决。
矩阵分解，是把原来的大矩阵，近似分解成两个小矩阵的乘积，并使用分解后的两小矩阵进行推荐计算。
用户物品矩阵：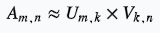
，维度 k 是隐因子，不一定具有可解释性。
矩阵分解的常见方法之一是奇异值分解:https://www.cnblogs.com/pinard/p/6251584.html
用于矩阵降维，可以得到维度较小的奇异值。
在推荐系统中实际使用的不是正统的奇异值分解，而是通过深度学习的训练方式计算小矩阵，如：
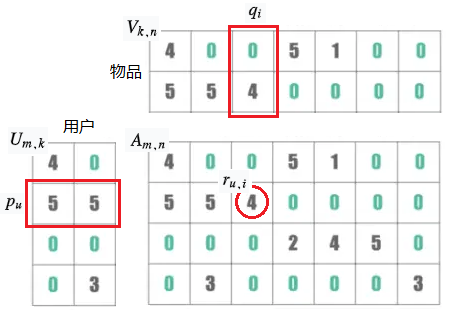
（1）基础的 SVD 算法：用户 u 的向量 p，物品 i 的向量 q，点积后的结果：
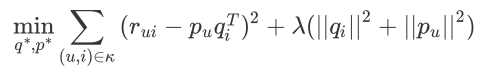
前一部分：用分解后的矩阵预测分数，和实际的用户评分之间误差越小越好；
后一部分：得到的隐因子向量要越简单越好，以控制模型的方差。
（2）增加偏置信息：为了减小用户评分的不一致的干扰，如铁粉的高评分等，则需要在用户和物品的评分偏置：
前一部分，从左到右是：μ全局平均分、b物品的评分偏置、b用户的评分偏置、用户和物品之间的兴趣偏好。
（3）增加历史行为：通常点评电影或美食的用户是少数，隐式反馈就较少，所以增加隐式反馈向量和用户属性向量：
（4）考虑时间因素：人会随着时间的变化而改变评价，对特殊的节日、周末、不同的时间区间分别学习隐因子向量。