二分查找,其原理思想也是如此的简单明了。但事实上,据Knuth描述,第一个木有bug的二分查找是这个算法发表之后12年在出现,但后来发现还是存在一些数组越界的小问题。而如今,我们大都是开门见山的学习被前辈们优化证明的算法,这也是“牛逼顿”所谓的站在巨人的肩膀上,却也如此。
回头来看二分查找如何“花式”卖萌。
Problem:给定一个有序数组A,且数组中的元素存在重复,给定一个目标值target,求目标值在数组的的下标的区间(即目标元素的起始下标和结束下标组成的区间)。
eg:
int a[9]={0, 1, 2, 3, 3, 3, 4, 5, 6 } ,给定target=3,则返回区间为[3 5].
分析:显然这必然会用到二分查找的思想,但要稍作修改。只要分别找到左边界和右边界下标即可。
左边界
版本一:
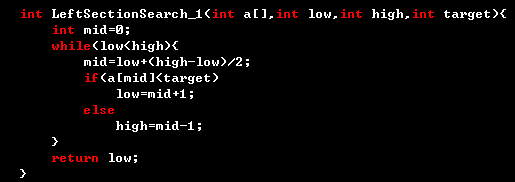
版本二:

事实上,写二分寻找左区间一般来说都不会有bug的,但是右区间就有点搞笑了。
右边界
版本一:

嗯,这个版本也没有问题,真是幸福!!
且慢,下面这个版本就显得有点任性了!
版本二:

运行之,死循环!应该说在某些情况下会死循环。
哪里有问题呢?
嗯,就是low=mid;的问题。
为什么呢?
因为当low+1等于high且a[mid]等于target时,mid等于low+(high-low)/2等于low;但是mid又赋值给了low,那么,结果是low和high都没有移动,“原地踏步”,循环往复。。。。。。
所以,这个版本就虾米了!
譬如:a1[9]={1,2,3,3,3,5,7,8,9};运行结果会挂掉!
a2[8]={1,3,3,3,5,7,8,9};运行结果会ok!
另外,用二分思想求区间右边界的的思想在另外一个小算法中也有体现。---------折半插入排序。
折半插入排序可以在保证排序结果稳定的前提下,减少直接插入排序的寻找如入位置的时间,但相对直接插入排序而言,也仅仅是减少了寻找插入位置的时间。但其思想还是可借鉴滴!
BY QCER
2015.10.2