【NOIP2020提高B组模拟11.26】卡常题

题目大意

ρ有一个二分连通无向图，X 方点、Y 方点均为n个（编号为1 ~ n）。
这个二分图比较特殊，每一个Y 方点的度为2，一条黑色边，一条白色边。
所有黑色边权值均为a ，所有白色边权值均为b 。
选择一个X 方点，代价为连接的所有边的权值之和。
激活一个Y 方点，需要选择至少一个与之相邻的X 方点。
现在，ρ想激活每个Y 方点，他想知道最小的总代价。
不过ρ很善良，他给你开了O2 优化。
这样你就不会被卡常了。
当然，除非你真的连读入优化都不想写，或者常数真的丑死。

解题思路

将Y类点变成一条边，点变成边权
转换成在一棵奇环树上，每一条边的两个端点至少选一个的最小代价
设f[i][0/1]表示以点i为根的子树全部处理好了，而点i没选/选了所花费的最小代价，那么转移显然
=

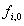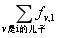
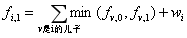
但是r1和r2之间必须选一个，所以再考虑设g[i][0/1]表示以点i为根的子树全部处理好了，且选了r2，而点i没选/选了所花费的最小代价，
转移同上，只不过g[r2][0]=g[r2][1]
ans=min(g[r1][0],f[r1][1]

#include<bits/stdc++.h>
using namespace std;
long long n,m,i,j,b[400005],mid,l,r,x,y,ans[400005],tot,v;
struct node
{
	long long a,b,c;
}s[400005];
bool cmp(node x,node y)
{
	if(x.a!=y.a)return x.a<y.a;
	else return x.c<y.c;
}
double x11(long long x,long long y)
{
	return(s[x].b-s[y].b)*1.0/(s[x].a-s[y].a);
}
double x1(long long x,long long y)
{
	return (s[x].b-s[y].b)*1.0/(s[y].a-s[x].a);
}
int main()
{
	//freopen("gas.in","r",stdin);
	//freopen("gas.out","w",stdout);
	scanf("%lld%lld",&n,&m);
	for(i=1;i<=n;i++)
	{
		scanf("%lld%lld",&s[i].a,&s[i].b);
		s[i].c=0;
	}
	for(i=1;i<=m;i++)
	{
		scanf("%lld%lld",&s[i+n].a,&s[i+n].b);
		s[i+n].c=i;
	}
	sort(s+1,s+n+m+1,cmp);tot=0;
	for(i=1;i<=n+m;i++)
	{
		if(s[i].c==0)
		{
			while(tot>1&&x1(b[tot],i)<x1(b[tot-1],b[tot]))tot--;
			tot++;b[tot]=i;
		}else
		{
			l=1;r=tot;x=0;
			while(l+1<r)
			{
				mid=(l+r)/2;
				if(x1(b[mid-1],b[mid])<(double)s[i].b)l=mid;
				else r=mid;
			}
			if(x1(b[l],b[r])>s[i].b)x=b[l];
			else x=b[r];
			ans[s[i].c]=max(ans[s[i].c],s[x].b-abs(s[x].a-s[i].a)*s[i].b);
		}
	}tot=0;
	for(i=n+m;i>=1;i--)
	{
		if(s[i].c==0)
		{
			while(tot>1&&x11(b[tot],i)<x11(b[tot-1],b[tot]))tot--;
			tot++;b[tot]=i;
		}else
		{
			l=1;r=tot;x=0;
			while(l+1<r)
			{
				mid=(l+r)/2;
				if(x11(b[mid-1],b[mid])<(double)s[i].b)l=mid;
				else r=mid;
			}
			if(x11(b[l],b[r])>s[i].b)x=b[l];
			else x=b[r];
			ans[s[i].c]=max(ans[s[i].c],s[x].b-abs(s[x].a-s[i].a)*s[i].b);
		}
	}
	for(i=1;i<=m;i++)
	{
		printf("%lld
",ans[i]);
	}
}
//本来题如其名，不卡常过不了，感谢良心OJ把时限加到了1s