A. Temporarily unavailable
题目
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Polycarp lives on the coordinate axis Ox and travels from the point x=a to x=b. It moves uniformly rectilinearly at a speed of one unit of distance per minute.
On the axis Ox at the point x=c the base station of the mobile operator is placed. It is known that the radius of its coverage is r. Thus, if Polycarp is at a distance less than or equal to r from the point x=c, then he is in the network coverage area, otherwise — no. The base station can be located both on the route of Polycarp and outside it.
Print the time in minutes during which Polycarp will not be in the coverage area of the network, with a rectilinear uniform movement from x=a to x=b. His speed — one unit of distance per minute.
Input
The first line contains a positive integer t (1≤t≤1000) — the number of test cases. In the following lines are written t test cases.
The description of each test case is one line, which contains four integers a, b, c and r (−108≤a,b,c≤108, 0≤r≤108) — the coordinates of the starting and ending points of the path, the base station, and its coverage radius, respectively.
Any of the numbers a, b and c can be equal (either any pair or all three numbers). The base station can be located both on the route of Polycarp and outside it.
Output
Print t numbers — answers to given test cases in the order they are written in the test. Each answer is an integer — the number of minutes during which Polycarp will be unavailable during his movement.
Example
inputCopy
9
1 10 7 1
3 3 3 0
8 2 10 4
8 2 10 100
-10 20 -17 2
-3 2 2 0
-3 1 2 0
2 3 2 3
-1 3 -2 2
outputCopy
7
0
4
0
30
5
4
0
3
Note
The following picture illustrates the first test case.
Polycarp goes from 1 to 10. The yellow area shows the coverage area of the station with a radius of coverage of 1, which is located at the point of 7. The green area shows a part of the path when Polycarp is out of coverage area.
思路
就是直接分类讨论,枚举出所有情况来,送分题
(code)
#include<bits/stdc++.h>
using namespace std;
int a,b,c,r;
int ans;
int T;
int main() {
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
cin>>T;
while(T--) {
ans=0;
cin>>a>>b>>c>>r;
if(a>b) swap(a,b);
int L=c-r,R=c+r;
if(L<=b&&R>=b&&L>=a) {
cout<<abs(L-a)<<'
';
continue;
} else if(L<=a&&R>=a&&R<=b) {
cout<<abs(b-R)<<'
';
continue;
} else if(R<a) {
cout<<b-a<<'
';
continue;
} else if(L>b) {
cout<<b-a<<'
';
continue;
} else if(L<=a&&R>=b) {
cout<<0<<'
';
continue;
} else if(L>=a&&R<=b) {
cout<<L-a+b-R<<'
';
continue;
}
}
return 0;
}
B2. K for the Price of One (Hard Version)
题目
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
This is the hard version of this problem. The only difference is the constraint on k — the number of gifts in the offer. In this version: 2≤k≤n.
Vasya came to the store to buy goods for his friends for the New Year. It turned out that he was very lucky — today the offer "k of goods for the price of one" is held in store.
Using this offer, Vasya can buy exactly k of any goods, paying only for the most expensive of them. Vasya decided to take this opportunity and buy as many goods as possible for his friends with the money he has.
More formally, for each good, its price is determined by ai — the number of coins it costs. Initially, Vasya has p coins. He wants to buy the maximum number of goods. Vasya can perform one of the following operations as many times as necessary:
Vasya can buy one good with the index i if he currently has enough coins (i.e p≥ai). After buying this good, the number of Vasya's coins will decrease by ai, (i.e it becomes p:=p−ai).
Vasya can buy a good with the index i, and also choose exactly k−1 goods, the price of which does not exceed ai, if he currently has enough coins (i.e p≥ai). Thus, he buys all these k goods, and his number of coins decreases by ai (i.e it becomes p:=p−ai).
Please note that each good can be bought no more than once.
For example, if the store now has n=5 goods worth a1=2,a2=4,a3=3,a4=5,a5=7, respectively, k=2, and Vasya has 6 coins, then he can buy 3 goods. A good with the index 1 will be bought by Vasya without using the offer and he will pay 2 coins. Goods with the indices 2 and 3 Vasya will buy using the offer and he will pay 4 coins. It can be proved that Vasya can not buy more goods with six coins.
Help Vasya to find out the maximum number of goods he can buy.
Input
The first line contains one integer t (1≤t≤104) — the number of test cases in the test.
The next lines contain a description of t test cases.
The first line of each test case contains three integers n,p,k (2≤n≤2⋅105, 1≤p≤2⋅109, 2≤k≤n) — the number of goods in the store, the number of coins Vasya has and the number of goods that can be bought by the price of the most expensive of them.
The second line of each test case contains n integers ai (1≤ai≤104) — the prices of goods.
It is guaranteed that the sum of n for all test cases does not exceed 2⋅105.
Output
For each test case in a separate line print one integer m — the maximum number of goods that Vasya can buy.
Example
input
8
5 6 2
2 4 3 5 7
5 11 2
2 4 3 5 7
3 2 3
4 2 6
5 2 3
10 1 3 9 2
2 10000 2
10000 10000
2 9999 2
10000 10000
4 6 4
3 2 3 2
5 5 3
1 2 2 1 2
output
3
4
1
1
2
0
4
5
思路
首先是一个简单的贪心,要想钱最少买最多的东西,肯定是单次买便宜的,贵的合在一起买
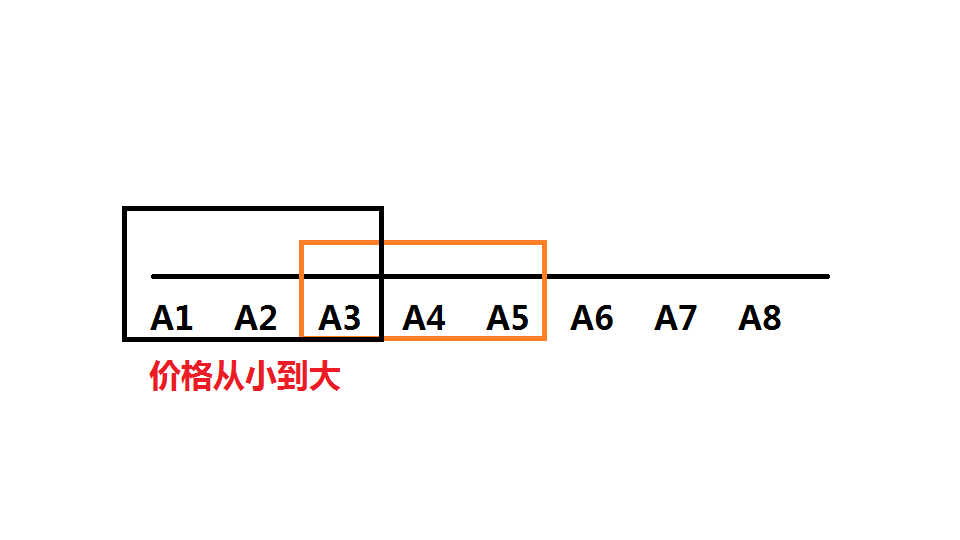
如上图橙色的合在一起买显然比黑色的合在一起买更划算
dp,用(f[i])表示购买前(i)个的最小花费
(f[i]=min(f[i-1]+val[i],f[i-k]+val[i]))
(code)
#include<bits/stdc++.h>
using namespace std;
//f[i]表示购买1~i的东西最少需要的价格
//f[i]=min(f[i-1]+a[i],f[i-k]+a[i])
const int N=2e5+2019;
int n,p,k,f[N],a[N];
int T;
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
cin>>T;
while(T--)
{
memset(f,0,sizeof(f));
cin>>n>>p>>k;
for(int i=1;i<=n;++i) cin>>a[i];
sort(a+1,a+1+n);
// f[1]=a[1];
for(int i=1;i<=n;++i)
{
f[i]=a[i];
if(i-k>=0) f[i]+=min(f[i-1],f[i-k]);
else f[i]+=f[i-1];
}
int ans=0;
for(int i=1;i<=n;++i)
if(f[i]<=p) ans=max(ans,i);
cout<<ans<<'
';
}
return 0;
}
剩下的我就不会了,(qwq)