树形DP学习笔记

概念：

树形dp就是....我也不知道是什么，反正一个主件下面有很多的附件可选就是树形dp，咕咕咕

dp方程 （并不适用于全部的树形dp）

树形dp的主要实现形式是dfs，在dfs中dp，主要的实现形式是dp[i]j，i是以i为根的子树，j是表示在以i为根的子树中选择j个子节点，0表示这个节点不选，1表示选择这个节点。有的时候j或0/1这一维可以压掉

选择节点类:

[dp[i][0]=dp[j][1] dp[i][1]=max/min(dp[j][0],dp[j][1])]

树形背包类:

[dp[v][k]=dp[u][k]+val dp[u][k]=max(dp[u][k],dp[v][k−1])]

其实我觉得就是这样的：
dp[i][j]并不表示以i为根，选j个物品，而是从根节点到i的路径及其左边所有的节点，以及以i为根的子树的所有节点中，容量为j的最大价值。上述方程应该用到了泛化物品的方法

泛化物品:

定义
考虑这样一种物品，它并没有固定的费用和价值，而是它的价值随着你分配给它的费用而变化。这就是泛化物品的概念。

更严格的定义之。在背包容量为V的背包问题中，泛化物品是一个定义域为0..V中的整数的函数h，当分配给它的费用为v时，能得到的价值就是h(v)。

这个定义有一点点抽象，另一种理解是一个泛化物品就是一个数组h[0..V]，给它费用v，可得到价值h[V]。

一个费用为c价值为w的物品，如果它是01背包中的物品，那么把它看成泛化物品，它就是除了h(c)=w其它函数值都为0的一个函数。如果它是完全背包中的物品，那么它可以看成这样一个函数，仅当v被c整除时有h(v)=v/cw，其它函数值均为0。如果它是多重背包中重复次数最多为n的物品，那么它对应的泛化物品的函数有h(v)=v/cw仅当v被c整除且v/c<=n，其它情况函数值均为0。

一个物品组可以看作一个泛化物品h。对于一个0..V中的v，若物品组中不存在费用为v的的物品，则h(v)=0，否则h(v)为所有费用为v的物品的最大价值。P07中每个主件及其附件集合等价于一个物品组，自然也可看作一个泛化物品。

泛化物品的和
如果面对两个泛化物品h和l，要用给定的费用从这两个泛化物品中得到最大的价值，怎么求呢？事实上，对于一个给定的费用v，只需枚举将这个费用如何分配给两个泛化物品就可以了。同样的，对于0..V的每一个整数v，可以求得费用v分配到h和l中的最大价值f(v)。也即

f(v)=max{h(k)+l(v-k)|0<=k<=v}

可以看到，f也是一个由泛化物品h和l决定的定义域为0..V的函数，也就是说，f是一个由泛化物品h和l决定的泛化物品。

由此可以定义泛化物品的和：h、l都是泛化物品，若泛化物品f满足以上关系式，则称f是h与l的和。这个运算的时间复杂度取决于背包的容量，是O(V^2)。

泛化物品的定义表明：在一个背包问题中，若将两个泛化物品代以它们的和，不影响问题的答案。事实上，对于其中的物品都是泛化物品的背包问题，求它的答案的过程也就是求所有这些泛化物品之和的过程。设此和为s，则答案就是s[0..V]中的最大值。

背包问题的泛化物品
一个背包问题中，可能会给出很多条件，包括每种物品的费用、价值等属性，物品之间的分组、依赖等关系等。但肯定能将问题对应于某个泛化物品。也就是说，给定了所有条件以后，就可以对每个非负整数v求得：若背包容量为v，将物品装入背包可得到的最大价值是多少，这可以认为是定义在非负整数集上的一件泛化物品。这个泛化物品——或者说问题所对应的一个定义域为非负整数的函数——包含了关于问题本身的高度浓缩的信息。一般而言，求得这个泛化物品的一个子域（例如0..V）的值之后，就可以根据这个函数的取值得到背包问题的最终答案。

综上所述，一般而言，求解背包问题，即求解这个问题所对应的一个函数，即该问题的泛化物品。而求解某个泛化物品的一种方法就是将它表示为若干泛化物品的和然后求之。（以上内容取自背包九讲）

上图取自国家集训队论文《浅谈几类背包题》，点击图片可以放大.

例题：

一.P2014 选课

传送门

思路

题目意思是想选择一门课，必须要先学会它的必修课，即选择一门课必须要选择必修课。那么他又说要选择的价值最大，这就是背包问题啦。又因为他有依赖性性行为,所以就是个树形dp
解释一下样例：

7  4
2  2
0  1
0  4
2  1
7  1
7  6
2  2

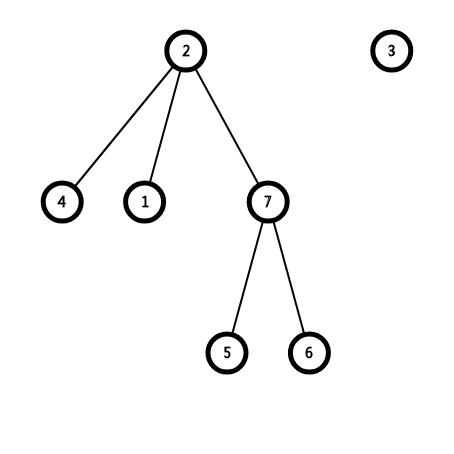
很明显此题的关联关系一目了然，所以我们可以在子树上适用范化背包.
注意爸爸是0说明没有爸爸
即：
设f[i][j]表示选择以i为根的子树中j个节点。
u代表当前根节点，sum代表其选择的节点的总额。

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<string>
#include<cstring>
#define ll long long int
#define MAXN 2500
using namespace std;
inline int read() {
	char c = getchar();
	int x = 0, f = 1;
	while(c < '0' || c > '9') {
		if(c == '-') f = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
	return x * f;
}
struct node {
	int next,to;
} e[MAXN];
int n,m,head[MAXN],c[MAXN],f[MAXN][MAXN],sum;
void add(int x,int y)
{
	e[++sum].next=head[x];	
	e[sum].to=y;
	head[x]=sum;
}
void build(int u,int t)
{
	if(t<=0) return;
	for(int i=head[u];i;i=e[i].next)
	{
		int v=e[i].to;
		for(int j=0;j<t;++j)
		{
			f[v][j]=f[u][j]+c[v];
		}
		build(v,t-1);
		for(int k=1;k<=t;++k)
		{
			f[u][k]=max(f[u][k],f[v][k-1]);
		}
	}
}
int main() {
	n=read(),m=read();
	for(int i=1; i<=n; ++i) 
	{
		int a;
		cin>>a>>c[i];
		if(a!=0) 
		{
			add(a,i);
		}
		if(a==0) 
		{
			add(0,i);
		}
	}
	build(0,m);
	cout<<f[0][m];
	return 0;
}

二.P1352 没有上司的舞会

链接：

传送门

思路：

这道题比上面的简单多了，咕咕咕，就是直接用第一个dp方程

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<string>
#include<cstring>
#define ll long long int
#define MAXN 6666
using namespace std;
const int maxn=999999999;
const int minn=-999999999;
inline int read() {
	char c = getchar();
	int x = 0, f = 1;
	while(c < '0' || c > '9') {
		if(c == '-') f = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
	return x * f;
}
/*
注释掉的有bug 
struct node {
	int next,to;
	int in;
} e[MAXN];
int n,m,happy[MAXN],head[MAXN],dp[MAXN][MAXN],root,sum;
void add(int x,int y) {
	e[++sum].next=head[x];
	e[sum].to=y;
	head[x]=sum;
}
void do_it(int x) {
	for(int i=head[x]; i; i=e[i].next) {
		do_it(i);
		dp[x][1]=max(max(dp[x][1],dp[x][1]+dp[i][0]),dp[i][0]);
		dp[x][0]=max(max(dp[x][0],dp[i][1]+dp[x][0]),max(dp[i][1],dp[i][0]));
	}
}
int main() {
	n=read();
	for(int i=1; i<=n; ++i ) happy[i]=read();
	for(int i=1; i<=n-1; ++i) {
		int x,y;
		cin>>x>>y;
		e[x].in++;
		add(y,x);
	}
	int zero1,zero2;//读掉0
	cin>>zero1>>zero2;
	for(int i=1; i<=n; ++i) {
		if(!e[i].in) {
			root=i;
			break;
		}
	}
	do_it(root);
	cout<<max(dp[root][0],dp[root][1]);
	return 0;
}
注释掉的有bug 
*/
int ind[MAXN],n,hap[MAXN],dp[MAXN][2],fa[MAXN],root,vis[MAXN],next[MAXN],po[MAXN];
void do_it(int x)
{
    for(int i = po[x]; i; i = next[i])
    {
        do_it(i);
        dp[x][1]=max(max(dp[x][1],dp[x][1]+dp[i][0]),dp[i][0]);
        dp[x][0]=max(max(dp[x][0],dp[i][1]+dp[x][0]),max(dp[i][1],dp [i][0]));
    }
}
int main()
{
    cin>>n;
    for(int i=1; i<=n; i++)
        cin>>dp[i][1];
    for(int i=1; i<=n; i++)
    {
        int a,b;
        cin>>b>>a;
        ind[b]++;
        next[b]=po[a];
        po[a]=b;
    }
    for(int i=1; i<=n; i++)
        if(!ind[i])
        {
            root=i;
            break;
        }
    do_it(root);
    cout<<max(dp[root][0],dp[root][1]);
}

这篇博客是我学习了网上的大佬和国家队徐持衡的论文后写的，奈何我的水平太低无法深入的学会，只是肤浅的懂了所以可能会有一些错误，如果发现请评论区告诉我！