[toc]
#推荐学习树状数组的博客:
1.[树状数组简单易懂的详解](https://blog.csdn.net/flushhip/article/details/79165701)
2.[可以代替线段树的树状数组?——树状数组进阶(1)](https://www.luogu.org/blog/Chanis/super-BIT)
#概念
树状数组顾名思义就是长得像树的数组(nm这还用你说)
先放张图看一下下:
这是一颗普通的二叉树
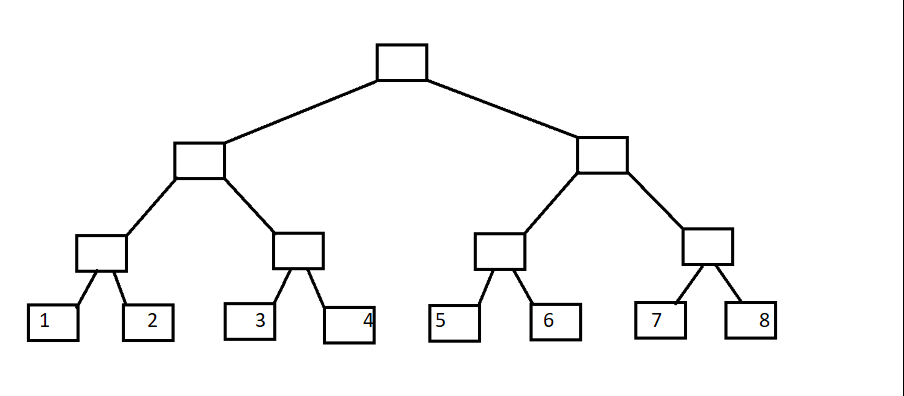
巴啦啦能量沙罗沙罗二叉树全身变:
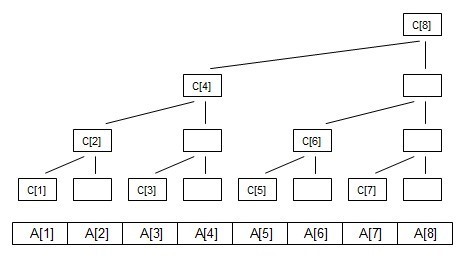
C[i]代表 子树的叶子结点的权值之和:
C[1]=A[1]; C[2]=A[1]+A[2]; C[3]=A[3]; C[4]=A[1]+A[2]+A[3]+A[4]; C[5]=A[5]; C[6]=A[5]+A[6]; C[7]=A[7]; C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
然后在把他们二进制表示一下:将每一个二进制,去掉所有高位1,只留下最低位的1,然后从那个数一直加到1
1=(001) C[1]=A[1] 2=(010) C[2]=A[1]+A[2] 3=(011) C[3]=A[3] 4=(100) C[4]=A[1]+A[2]+A[3]+A[4] 5=(101) C[5]=A[5] 6=(110) C[6]=A[5]+A[6]; 7=(111) C[7]=A[7] 8=(1000) C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]
C[i]=A[i-2^k+1]+A[i-2^k+2]......+A[i] (k为i的二进制中从最低位到高位连续零的长度)
模板:
lowbit:
#define lowbit(i) i&-i
lowbit(x) 其实就是取出x的最低位1 也就是 lowbit(x)=2^k
区间查询:
就是前缀和,比如查询x到y区间的和,那么就将从1到y的和-从1到x的和。
从1到y的和求法是,将y转为2进制,然后一直减去lowbit(y),一直到0
l find(int x) { ll kkk=0; for(int i=x; i; i-=lowbit(i)) { kkk+=t[i]; } return kkk; }
单点修改:
而如果改变x的值,就要加上自己的lowbit,一直加到n,这些节点都要加,比如一共有8个数第3个数要加上k,那么c[0011]+=k;
c[0011+0001] (c[0100])+=k;
c[0100+0100] (c[1000])+=k;
这样就能维护树状数组
void insert(int x,int y) { for(int i=x; i<=n; i+=lowbit(i)) { t[i]+=y; } }
区间修改
这就会变的很好玩。如果将x到y区间加上一个k,那就是从x到n都加上一个k,再从y+1到n加上一个-k
加的移动还是i+=lowbit(i);
void add(int x,int k) { while(x<=n) { tree[x]+=k; x+=lowbit(x); } }
例题:
P3374 【模板】树状数组 1
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<queue> #include<stack> #include<vector> #include<map> #include<string> #include<cstring> #define ll long long int #define lowbit(i) i&-i #define MAXN 500050 using namespace std; const int maxn=999999999; const int minn=-999999999; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); } while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } ll t[MAXN],a[MAXN],b[MAXN],ans,n,m; ll find(int x) { ll kkk=0; for(int i=x; i; i-=lowbit(i)) { kkk+=t[i]; } return kkk; } void insert(int x,int y) { for(int i=x; i<=n; i+=lowbit(i)) { t[i]+=y;; } } int main() { n=read(),m=read(); for(int i=1; i<=n; ++i) cin>>a[i],insert(i,a[i]); while(m--) { int p,xx,yy; cin>>p>>xx>>yy; if(p==1) insert(xx,yy); else if(p==2) cout<<find(yy)-find(xx-1)<<' '; } return 0; }
P3368 【模板】树状数组 2
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<queue> #include<stack> #include<vector> #include<map> #include<string> #include<cstring> #define ll long long int #define MAXN 500001 #define lowbit(i) i&-i using namespace std; const int maxn=999999999; const int minn=-999999999; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); } while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int t[MAXN],a[MAXN],n,m,ans,last,d[MAXN]; int find(int x) { //单点查询 int aans=0; /*while(x) { aans+=t[x]; x-=lowbit(x); }*/ for(int i=x; i; i-=lowbit(i)) { aans+=t[i]; } return aans; } void insert(int x,int y) { for(int i=x; i<=n; i+=lowbit(i)) { t[i]+=y; } } int main() { n=read(); m=read(); for(int i=1; i<=n; ++i) { cin>>a[i];
/*这里很重要*/
/*
这里运用了差分思想,假设原本的数据存在a数组中,
那么c数组储存的就是c[i]=a[i]-a[i-1],如果c[1]=a[1],那么很明显
a[i]=c[i]+c[i-1]+c[i-2]+...+c[2]+c[1].
这样我们每次单点查询的时候只要加上c数组的前缀就可以了。
*/
d[i] = a[i] - a[i-1]; insert(i, d[i]); } while(m--) { int f,xx,yy,zz; cin>>f; if(f==1) { cin>>xx>>yy>>zz; insert(xx,zz); insert(yy+1,-zz);//把多的部分删掉 } else if(f==2) { cin>>xx; cout<<find(xx)<<' '; } } return 0; }
出处:
https://blog.csdn.net/Small_Orange_glory/article/details/81290634)