1、挖地雷(lei.cpp)时空限制1000ms / 128MB
题目描述
在一个地图上有NN个地窖(N≤20),每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径。当地窖及其连接的数据给出之后,某人可以从任一处开始挖地雷,然后可以沿着指出的连接往下挖(仅能选择一条路径),当无连接时挖地雷工作结束。设计一个挖地雷的方案,使某人能挖到最多的地雷。
输入格式:(lei.in)
有若干行。
第1行只有一个数字,表示地窖的个数N。
第2行有N个数,分别表示每个地窖中的地雷个数。
第3行至第N+1行表示地窖之间的连接情况:
第3行有n-1个数(0或1),表示第一个地窖至第2个、第3个、…、第n个地窖有否路径连接。如第3行为11000…0,则表示第1个地窖至第2个地窖有路径,至第3个地窖有路径,至第4个地窖、第5个、…、第n个地窖没有路径。
第4行有n-2个数,表示第二个地窖至第3个、第4个、…、第n个地窖有否路径连接。
… …
第n+1行有1个数,表示第n-1个地窖至第n个地窖有否路径连接。(为0表示没有路径,为1表示有路径)。
输出格式:(lei.out)
有两行
第一行表示挖得最多地雷时的挖地雷的顺序,各地窖序号间以一个空格分隔,不得有多余的空格。
第二行只有一个数,表示能挖到的最多地雷数。
输入输出样例
输入样例#1:
5 10 8 4 7 6 1 1 1 0 0 0 0 1 1 1
输出样例#1:
1 3 4 5 27
【思路】:
就是直接用dp,用f[i]表示从i挖能挖到的最多的地雷,f[i]=max(f[i],f[j])
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<queue> #include<stack> #include<vector> #include<map> #include<string> #include<cstring> using namespace std; const int maxn=999999999; const int minn=-999999999; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); } while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int n,pre[215],a[215],g[215][215],ans,t,f[215]; void print(int x) {//递归输出路径 if(pre[x]==0) { printf("%d",x); return ; } print(pre[x]); printf(" %d",x);//注意空格问题 } int main() { freopen("lei.in","r",stdin); freopen("lei.out","w",stdout); n=read(); for(int i=1; i<=n; ++i) {//读入地雷 scanf("%d",a+i); } for(int i=1; i<=n; ++i) { for(int j=i+1; j<=n; ++j) { int x=read(); if(x==1) g[i][j]=1;//存是否存在路径 } } for(int i=1; i<=n; ++i) { for(int j=1; j<=n; ++j) { if((g[j][i]==1)&&(f[j]>f[i])) { f[i]=f[j]; pre[i]=j; } } f[i]+=a[i]; if (f[i]>ans) { ans=f[i]; t=i; } } print(t); cout<<' '; printf("%d",ans); fclose(stdin); fclose(stdout); return 0; }
题目背景
一年一度的“跳石头”比赛又要开始了!
题目描述
这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 N 块岩石(不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达终点。
为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走 M 块岩石(不能移走起点和终点的岩石)。
输入输出格式
第一行包含三个整数 L,N,M,分别表示起点到终点的距离,起点和终点之间的岩石数,以及组委会至多移走的岩石数。保证 L≥1 且 N≥M≥0。
接下来 N 行,每行一个整数,第 i 行的整数Di(0<Di<L), 表示第 i 块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同一个位置。
输入输出样例
说明
输入输出样例 1 说明:将与起点距离为 2和 14 的两个岩石移走后,最短的跳跃距离为 4(从与起点距离 17的岩石跳到距离 21 的岩石,或者从距离 21 的岩石跳到终点)。
另:对于 20%的数据,0 ≤ M ≤ N ≤ 10。
对于50%的数据,0 ≤ M ≤ N ≤ 100。
对于 100%的数据,0 ≤ M ≤ N ≤ 50,000,1 ≤ L ≤ 1,000,000,000。
【思路】:
用二分答案来求。
至于为什么用二分答案?学长说过只要出现上面加粗的字就用,嘿嘿
为什么能用二分答案?
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<queue> #include<stack> #include<vector> #include<map> #include<string> #include<cstring> using namespace std; const int maxn=999999999; const int minn=-999999999; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); } while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int a[2000002],mid,l,r,ans,L,N,M,now_juli,js; int check(int x) { now_juli=0,js=0; /*js是表示搬走的石头数量,now_juli是当前的石头离起点的距离*/ for(int i=1; i<=N+1; ++i) { if(a[i]-now_juli<x) { //比较两点之间的距离 js++; } else { now_juli=a[i]; } } if(js>M) return 0; } int main() { // freopen("stone.in","r",stdin); // freopen("stone.out","w",stdout); scanf("%d%d%d",&L,&N,&M); if(N==0&&M==0) { cout<<L; return 0; } int l=0,r=L;//初始化二分边界 for(int i=1; i<=N; i++) scanf("%d",&a[i]); /*注意输入距离从近到远,答案有单调性*/ a[N+1]=L;//注意设置终点,呜呜呜浪费我20分钟查错误 while(l<=r) { mid=(l+r)/2; if(check(mid)) { //右 l=mid+1; ans=mid; } else { //左 r=mid-1; } } cout<<ans; fclose(stdin); fclose(stdout); return 0; }
3、花匠flower.cpp(时空限制1000ms / 128MB)
题目描述
花匠栋栋种了一排花,每株花都有自己的高度。花儿越长越大,也越来越挤。栋栋决定把这排中的一部分花移走,将剩下的留在原地,使得剩下的花能有空间长大,同时,栋栋希望剩下的花排列得比较别致。
具体而言,栋栋的花的高度可以看成一列整数h1,h2,...,hn。设当一部分花被移走后,剩下的花的高度依次为g1,g2,...,gm,则栋栋希望下面两个条件中至少有一个满足:
条件 A:对于所有g2i>g2i−1,g2i>g2i+1
条件 BB:对于所有g2i<g2i−1,g2i<g2i+1
注意上面两个条件在m=1时同时满足,当m > 1时最多有一个能满足。
请问,栋栋最多能将多少株花留在原地。
输入输出格式
输入格式:
第一行包含一个整数n,表示开始时花的株数。
第二行包含n个整数,依次为h1,h2,...,hn,表示每株花的高度。
输出格式:
一个整数m,表示最多能留在原地的花的株数。
输入输出样例
输入样例flower.in
5 5 3 2 1 2
输出样例flower.out
3
说明
【输入输出样例说明】
有多种方法可以正好保留 3 株花,例如,留下第 1、4、5 株,高度分别为 5、1、2,满足条件 B。
【数据范围】
对于 20%的数据,n ≤ 10;
对于30%的数据,n ≤ 25;
对于 70%的数据n≤1000,0≤hi≤1000;
对于100%的数据,1≤n≤100,000,0≤hi≤1,000,000,所有的hi随机生成,所有随机数服从某区间内的均匀分布。
【思路】:和合唱队形一样的思路。用二维数组表示到i点的最长上升和最长下降.
然后统计波峰和波谷
当出现这种情况时波谷+1(波谷怎么记录下面会有)
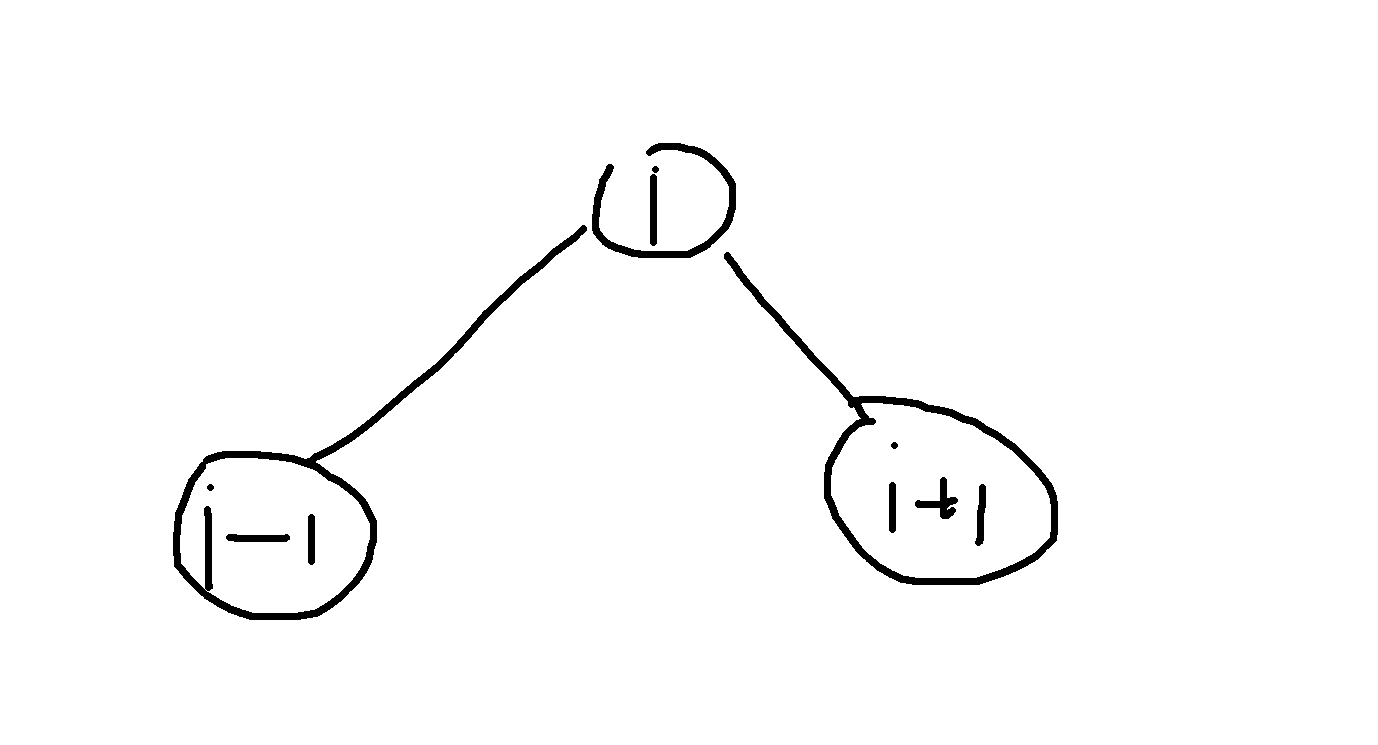
当出现这个情况时波峰加1

至于最后一种情况
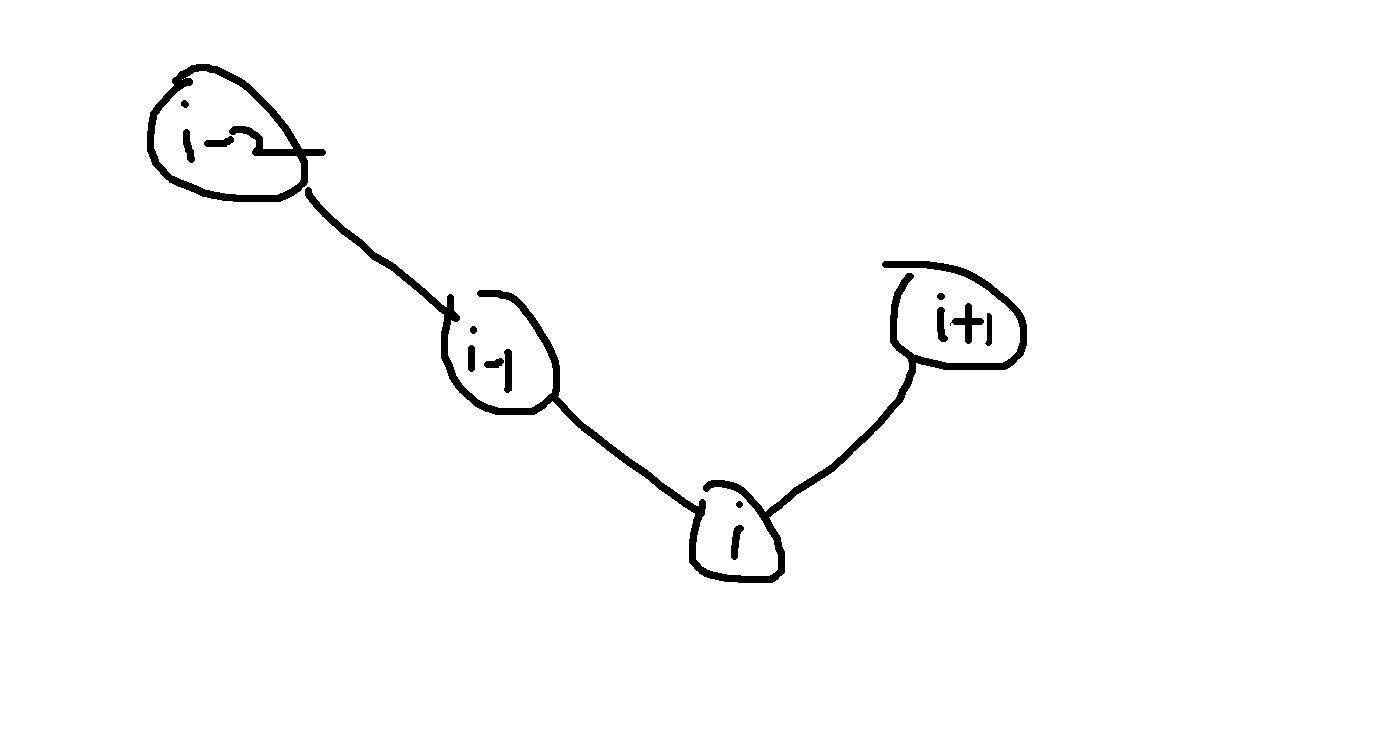
看i-2和i-1两个花,明显是不合法的,所以继续保留之前的结果就行了
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<queue> #include<stack> #include<vector> #include<map> #include<string> #include<cstring> using namespace std; const int maxn=999999999; const int minn=-999999999; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); } while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int n; int a[1000800],on[100800],down[100800]; int main() { n=read(); for(int i=1; i<=n; ++i) { a[i]=read(); } on[1]=1,down[1]=1; for(int i=2; i<=n; ++i) { if(a[i]>a[i-1]) on[i]=down[i-1]+1; else on[i]=on[i-1]; if(a[i]<a[i-1]) down[i]=on[i-1]+1; else down[i]=down[i-1]; } cout<<max(on[n],down[n]); return 0; }