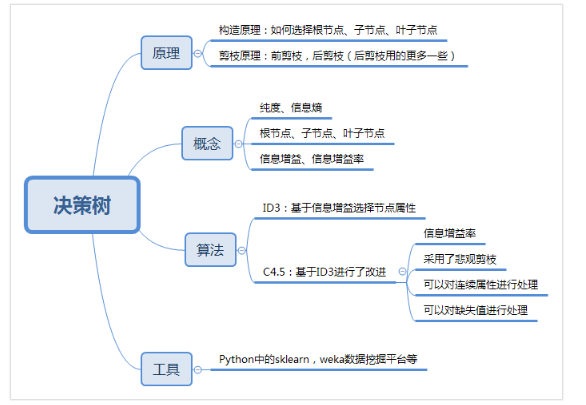
决策树基于时间的各个判断条件,由各个节点组成,类似一颗树从树的顶端,然后分支,再分支,每个节点由响的因素组成
决策树有两个阶段,构造和剪枝
构造: 构造的过程就是选择什么属性作为节点构造,通常有三种节点
1. 根节点:就是树的最顶端,最开始那个节点 (选择哪些属性作为根节点)
2. 内部节点: 就是树中间的那些节点 (选择哪些属性作为子节点)
3. 叶节点: 就是树最底部的节点,也就是决策的结果(什么时候停止并得到目标状态,叶节点)
剪枝: 实现不需要太多的判断,同样可以得到不错的结果,防止过拟合现象发生
过拟合百度百科直观了解一下(https://baike.baidu.com/item/%E8%BF%87%E6%8B%9F%E5%90%88/3359778)
简单介绍就是为了得到一致假设而使假设变得过度严格称为过拟合。
预剪枝是在决策树构造前进行剪枝,在构造过程中对节点进行评估,如果某个节点的划分,在验证集中不能带来准确性的提升,划分则无意义当成叶节点不做划分
后剪枝是在生成决策树后再进行剪枝,通常会从决策树的叶节点开始,逐层向上对每个节点进行评估,减掉与保留差准确性差别不大,或者减掉改节点字数,能在验证集中带来准确性提升,就可以剪枝。
信息熵: 表示了信息的不确定度,下面是计算公式,信息熵越大纯度越低
当不确定性越大,包含的信息量就越大,信息熵就越高
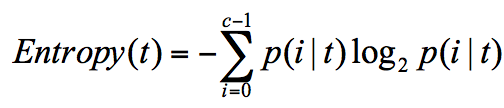
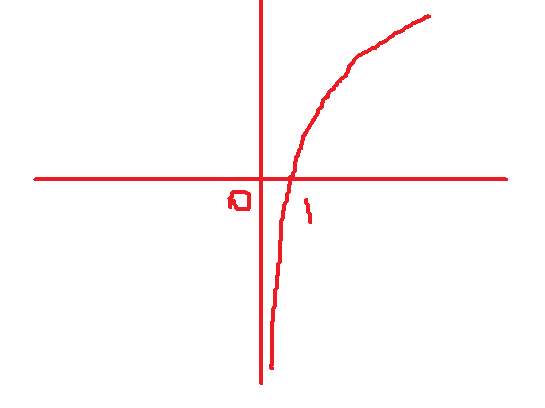
(log 函数图像也可以理解 ,下面函数0到1 之间对应的是概率,当概率接近1的时候,说明纯度很高(概率),纵坐标值很小,
信息熵很小,当概率接近0的时候,纯度很低,信息熵就很大了,注意,这里是负值,公式前面也有个负号,然后合并就为正)
信息增益:ID3 算法 指划分可以带来纯度的提高,信息熵的下降,父节点的信息熵减去所有子节点的信息熵,计算过程中,会计算子节点归一化的信息熵 下面是计算公式
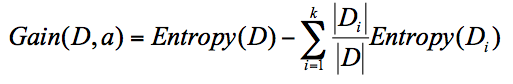
公式中D是父亲节点,Di 是子节点,Gain(D,a) 中的a作为D节点的属性选择
归一化子节点的信息熵,就是公式中的Di/D 信息增益最大可以作为父亲节点,再重复进行判断到最后得出
C4.5算法
1 采用信息增益率 信息增益率 = 信息增益/属性熵 信息增益的同事,属性熵也会变大
2 采用悲观剪枝 ID3 中容易产生过拟合现象, 这个方法可以提升决策树的泛华能力,属于后剪枝的一种,比较剪枝前后这个节点的分类错误率来觉得是否对其进行剪枝
3 离散化处理连续属性 C4.5可以处理连续属性的情况,对连续属性进行离散化处理,就是对值进行计算,而不是分为几等分(高,中,底) C4.5 选择具有最高信息增益的划分所对应的阈值
4 处理缺失值 C4.5 也可以处理,假如数据集存在较少的缺失值, 对子节点归一化计算信息增益,然后计算信息增益率,由于有对应的缺失值,所以信息增益率*占权比重,(比如7个数据,少了一个*6/7)所以在属性确实的情况下也可以计算信息增益
ID3和C4.5比较, ID3算法简单,确定是对噪声敏感,少量错误会产生决策树的错误,C4.5 进行了改进,长上面可以看出,但是C4.5 需要对数据集进行多次扫描,算法效率相对较低