求坐标精度:
https://www.cnblogs.com/pylblog/p/10464467.html
由泰勒展开式到微分:
一阶展开
Z = f(x1,x2,...xn) = f(x10 , x20, ...xn0) + δf / δx1 * (x1 -x10) + ... δf / δxn * (xn -xn0)
Z - f(x10 , x20, ...xn0) = dZ = δf / δx1 * dx1 + ... δf / δxn * dxn
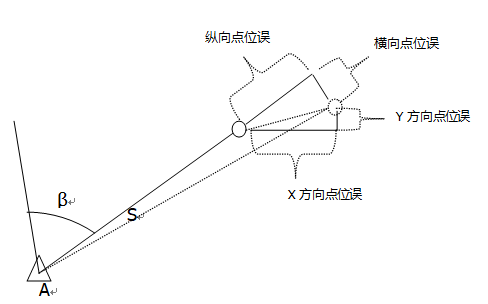
Xc = XA + S * Cos(aAC)
Yc = YA + S * Sin(aAC)
σc2 = σxc2 + σyc2 又等于 σc2 = σs2 + σβ2
假如A已知,也就是无误差
dXc = cos(aAC) dS - S * sin(aAC) * daAC / ρ (daAC 是一个角度单位,度或分、秒)
dYc = sin(aAC) dS + S * cos(aAC) * daAC / ρ
因为测角、距是相互独立的,所以由误差传播,可得
σxc2 = cos2(aAC) σs2 + (S/ρ)2 sin2(aAC) σAC2
σyc2 = sin2(aAC) σs2 + (S/ρ)2 cos2(aAC) σAC2
σc2 = σxc2 + σyc2 = σs2 + ( (S / ρ) σAC )2
纵向误差:σs
横向误差:(S / ρ) σAC
关于定权
有L1~L6个等精度观测的、相互独立的观测值,精度为σ,分别由两人观测
甲观测了:L1、L2 甲提交观测值:X甲 = (L1 + L2)/ 2 精度:σ甲 = σ / √2
乙观测了:L3、L4、L5、L6 乙提交观测值:X乙 = (L3 +.. + L6)/ 4 精度:σ甲 = σ / √4
那么,如果都是同一人观测的,结果可为:
X = (L1 + ..... + L6) / 6
但现在要从甲、乙两方提交的成果考虑,那么:
X = ( 2X甲 + 4X乙 )/ (2 + 4)
2 = σ2 / σ甲 2
4 = σ2 / σ乙 2
回代:
X = ( σ2 / σ甲 2 * X甲 + σ2 / σ乙 2 * X乙 )/ ( σ2 / σ甲 2 + σ2 / σ乙 2)
p甲 = σ2 / σ甲 2 (权越大,精度越好)
那么:
X = ( p甲 X甲 + p乙 X乙 )/ (p甲 + p乙 )
由上式可知:
X = ( 1 / σ甲 2 * X甲 + 1 / σ乙 2 * X乙 )/ ( 1 / σ甲 2 + 1 / σ乙 2)
σ 可以为任意值,不影响X的计算结果