神经网络训练的优化操作

1. 输入特征值x的归一化。

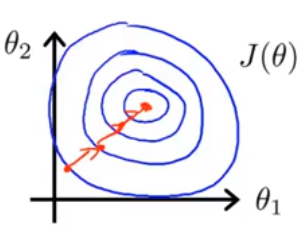
如果有(x1,x2)，x1的取值范围是[0~1]，而x2是[0~2000]，那么会造成损失函数J(θ)的形状：

(J(θ)的等高线图)

在求J(θ)最小值时，对θ1和θ2反向传播，修改值时，往往使得修改的方向震荡。

改进办法是，将x1和x2的取值范围，规定在差不多的范围内，通常在[0,1]区间，得到J(θ)等高线图：

办法：

x_i = (x_i - avg(x)) / (x_max - x_min)

2. 损失函数正规化

在实际中，如果有x₁……x_n 多个特征，有的x_m  = x_ix_j 或者 x_m = x_i⁴ 这样的特征组合而成的新特征，有用，但是不是十分重要的话（要视具体问题而定），如果对应的θ_m 偏大的话，往往会产生过拟合问题。

例如：

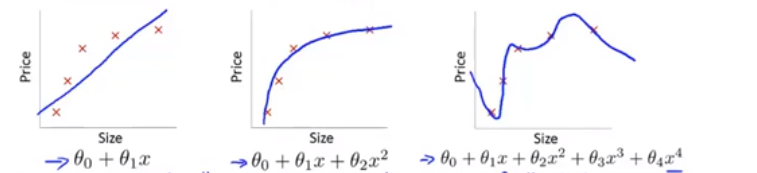（欠拟合，刚好拟合，过拟合）

对于损失函数，如果J(θ) = 1 / 2n ∑(h_θ(x) - y ) + 1000 * θi  + 1000 * θ_j   （假设θi和θ_j 是无关紧要的特征的权值）

那么，根据反向传播 θ_i = θ_i - a * d(J(θ)) / dθi , d(J(θ)) / dθ_i  为一个大数，也就是θ_i 被"惩罚"得特别厉害。

正规的方程应该为：

J(θ) = 1 / 2n * [ ∑(h_θ(x) - y )² + λ ∑ θ² ]

θ_i = θ_i(1 - a*λ/n) + a/m * (∑(h_θ(x) - y )) *x_i （当h_θ(x) = θ^TX）

原来是：θ_i = θ_i+ a/m * (∑(h_θ(x) - y )) *x_i

1 - a*λ/n 接近于1。也就是说，每次更新，都会先对原来的θ进行缩小

注意，如果λ过大，会导致每个θ过小，最终拟合出一条水平直线出来。